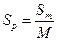Что называют основанием масштаба
Масштабы



Масштабы.
Понятие карты, плана, профиля.
При изображении физической поверхности Земли на картах её проектируют на поверхность эллипса, а затем его разворачивают в плоскость. Таким образом, картой называют уменьшенное и закономерно искаженное изображение Земли или отдельных частей её поверхности на плоскости.
На топографических картах все объекты земного изображаются максимальной точностью, независимо от значимости объекта.
Стандартные масштабы
Масштабы топокарт: Масштабы планов:
Так, при аЬ=5см и АоВо=250м имеем
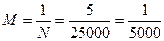
При сравнении численных масштабов различных планов употребляют термины: «мельче» и «крупнее». Если N1
Линейный масштаб используют для измерения с небольшой точностью длин отрезков на плане. Он представляет собой прямую линию, разделенную на равные отрезки. Длина одного отрезка называется основанием масштаба. Она соответствует определенному числу метров на горизонтальном проложении. На рисунке 1.3 основание принято равным 2см, что при численном масштабе 1:5000 соответствует 100м на горизонтальном проложении. Левое крайнее основание линейного масштаба разделено на более мелкие деления.
Рис.1.3 Линейный масштаб
Поперечный масштабприменяют для измерений и построений повышенной точности. Для каждого масштаба можно построить свой поперечный масштаб. Поперечный масштаб с основанием 2см называется нормальным сотенным поперечным масштабом, то есть пригодным для любого масштаба.
Поперечный масштаб строят следующим образом:
На прямой линии откладывают ряд отрезков по 2см, которые называют основанием масштаба. Из концов оснований восстанавливают перпендикуляры произвольной длины. На крайних перпендикулярах измерителем откладывают по 10 отрезков одинаковой длины и соединяют их концы. Крайнее левое основание сверху и снизу делят на 10 одинаковых частей методом деления отрезка на пропорциональные части. Затем соединяют верхние и нижние точки (рис. 1.4)
|
Для пользования поперечным масштабом необходимо мысленно оцифровать его деления исходя из масштаба плана или карты. Так если масштаб плана1:5OO, то основанием равно 10м деление равно 1 м и наименьшее деление 0,1м.
Измеритель располагают таким образом, чтобы правая игла находилась на одной из вертикальных линий, а левая на трасверсале. После чего считают,
 |
сколько целых (к), десятых (п) и сотых (i) долей основания содержится между углами и исходя из ранее выполненной оцифровки, вычисляют расстояние.
Для случая приведенного на рис. 1.5 имеет к=1; п=4; i=3,5 масштаб 1:500, а следовательно:
S=1 * 100+4(0,1 * 100)+3,5(0,01 * 100)=143,5м
Невооруженный глаз человека способен на чертеже, на расстоянии 20-25см увидеть точку равную 0,1мм. Поэтому точностью масштаба называют длину горизонтальной проекции на местности, соответствующую 0,1мм на карте или плане. Для масштаба 1:500; 1:1000; 1:10000; 1:25000; точность масштаба соответственно равно 0,05м; 0,1м; 1,0м; 2,5м.
Пример1. Дано расстояние между двумя точками на карте равное 56,4мм. Определить длину горизонтального проложения соответствующей линии местности, если масштаб карты равен 1:2000.
Решение. Вычисление производится по формуле
где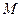
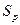
Пример2. Дано горизонтальное проложение линий местности равное 78,0м. Определить с точностью 0,1 мм длину соответствующей линии на карте в масштабе 1:2 000
Решение. Вычисление выполняют по формуле:
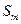
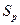
Пример3. Определить длину отрезка на плане масштаба 1:1000, если длина линии на местности равна 35.6м.
Так же как и в предыдущей задаче необходимо мысленно оцифровать деления поперечного масштаба. Так, если масштаб плана 1:1000, то основание поперечного масштаба равно 20 м., АВ=2м и наименьшее деление (а1 в1) равно 0.2м. А затем суммированием этих отрезков набрать длину линии на поперечном масштабе. Т.е.35.6:20м =1 (целое основание масштаба). Осталась длина линии 15.6. Ее делим на цену деления основания масштаба 15.6:2м=7 (целых делений основания масштаба. 7х2м=14м. 15.6-14м=1.6м. 1.6м:0.2м=8 (наименьших делений масштаба). После этого устанавливаем измеритель на поперечном масштабе так, чтобы между иголками измерителя уложилось 1 целое основание масштаба, 7 целых целений основания масштаба и 8 наименьших делений масштаба.
Пример4.На карте масштаба 1:2000 был измерен отрезок, длинной 2.5 см. Найти длину линии на местности, соответствующую этому отрезку.
Пример5. Найти длину отрезка на плане масштаба 1:500, если длина горизонтального проложения линии на местности 28.50м.
В масштабе 1:500 1см на плане соответствует 5м на местности. По условию задачи на местности 28.5м. Следовательно
Пример6.Определить точность масштаба 1:10 000.
Решение. Так как точность масштаба это длина горизонтальной проекции линии на местности, соответствующая 0.1мм на карте или плане, необходимо вычислить длину линии на местности, соответствующую 0.1мм на карте или плане. По аналогии с предыдущими задачами рассуждаем так 1см на карте масштаба 1:10 000 соответствует 100м на местности, соответственно
Пример7: Перевести численный масштаб 1:10000 в пояснительный.
Решение : Для перевода численного масштаба в пояснительный необходимо от сантиметров в знаменателе перейти к метрам;
Вопросы для самопроверки:
1. Что изучает геодезия?
3. Какие задачи решает инженерная геодезии?
4. Что представляет собой действительная фигура Земли?
5. Почему изображение фигуры Земли заменяют референц-эллипсоидом или шаром?
6. Что такое уровенная поверхность?
7. Что называется планом?
8. Что называется картой?
9. В чем отличия между картой и планом?
10. Что называется профилем местности?
11. Что называется масштабом?
12. Что представляют собой численный и пояснительный масштабы?
13. Перечислите масштабы топографических карт и планов.
14. Что такое точность масштаба?
15. Как построить нормальный сотенный поперечный масштаб?
Масштаб
Понятие наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения. Человек не в состоянии изобразить большие объекты, например, дом, в натуральную величину, поэтому, при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Содержание
Масштаб в геодезии, картографии и проектировании
Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.
Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность — 0,1.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Масштабы изображений на чертежах должны выбираться из следующего ряда: [1]
| Масштабы уменьшения | 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1 000 |
| Натуральная величина | 1:1 |
| Масштабы увеличения | 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1 |
При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
Масштаб в фотографии
При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Масштаб имеет важное значение при расчете глубины резко изображаемого пространства. Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Под макрофотографией традиционно понимают съёмку в масштабе 1:1 или крупнее. Однако с широким распространением компактных цифровых фотоаппаратов этим термином стали также называть съёмку расположенных близко к объективу (как правило, ближе 50 см) мелких объектов. Связано это с необходимым изменением режима работы системы автофокуса в таких условиях, однако с точки зрения классического определения макросъёмки такое толкование является неверным.
Масштаб в моделизме
Для каждого вида масштабного (стендового) моделизма определены масштабные ряды, состоящие из нескольких масштабов разной степени уменьшения, причём для разных видов моделизма (авиамоделизм, судомоделизм, железнодорожный, автомобильный, военной техники) определены свои, исторически сложившиеся, масштабные ряды, которые обычно не пересекаются.
Масштаб в моделизме исчисляется по формуле:
При масштабе 1/72, и параметре оригинала 7500 мм, решение будет выглядеть;
7500 мм / 72 = 104,1 мм
Полученное значение 104,1 мм, есть искомое значение при масштабе 1/72
Масштаб времени
В программировании
В операционных системах с разделением времени чрезвычайно важную роль играет предоставление отдельно взятым задачам так называемого «режима реального времени», при котором обработка внешних событий обеспечивается без дополнительных задержек и пропусков. Для этого употребляется также термин «реальный масштаб времени», однако это терминологическая условность, не имеющая к исходному значению слова «масштаб» никакого отношения.
В кинотехнике
Масштаб времени — количественная мера замедления или ускорения движения, равная отношению проекционной частоты кадров к съёмочной. Так, если проекционная частота кадров равна 24 кадра в секунду, а киносъёмка производилась на 72 кадра в секунду, масштаб времени равен 1:3. Масштаб времени 2:1 означает ускоренное вдвое по сравнению с обычным протекание процесса на экране.
В математике
Масштабы изображений на чертежах должны выбираться из следующего ряда (масштабы ГОСТ 2.302-68): Масштабы уменьшения 1 : 2; 1 : 2,5; 1 : 4; 1 : 5; 1 : 10; 1 : 15; 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000 Натуральная величина 1 : 1 Масштабы увеличения 2 : 1; 2.5,5 : 1; 4 : 1; 5 : 1; 10 : 1; 20 : 1; 40 : 1; 50 : 1; 100: 1 см. например Быстро-медленная система
Масштаб-число,показывающее, во сколько раз уменьшены или увеличены настоящие размеры на чертеже.
Что называют основанием масштаба
Различают численный, линейный и именованный масштабы.
Численный масштаб изображается в виде дроби, у которой числитель равен единице, а знаменатель – число, показывающее, во сколько раз уменьшены линии на карте (плане) относительно линий на местности. Например, масштаб 1:100 000 показывает, что все линейные размеры на карте уменьшены в 100 000 раз. Очевидно, чем больше знаменатель масштаба, тем масштаб мельче, при меньшем знаменателе — крупнее. Численный масштаб – это дробь, поэтому числитель и знаменатель даются в одинаковых измерениях (сантиметрах).
Линейный масштаб представляет собой прямую линию, разделенную на равные отрезки. Эти отрезки соответствуют определенному расстоянию на изображаемой местности; деления обозначаются цифрами. Мера длины, по которой нанесены деления на масштабной линейке, называются основанием масштаба. В нашей стране основание масштаба принято равным 1 см. Количество метров или километров, соответствующее основанию масштаба, называют величиной масштаба. При построении линейного масштаба цифру 0, от которой начинается отсчет делений, обычно ставят не у самого конца масштабной линии, а отступив на одно деление (основание) вправо; на первом же отрезке налево от 0 наносят наименьшие деления линейного масштаба – миллиметры. Расстояние на местности, соответствующее одному наименьшему делению линейного масштаба, отвечает точности масштаба, а 0,1 мм – предельной точности масштаба. Линейный масштаб по сравнению с численным имеет то преимущество, что дает возможность без дополнительных вычислений определять действительное расстояние на плане и карте.
Именованный масштаб – масштаб, выраженный словами, например, в 1 см 32 км.
Измерение расстояний на карте и плане.
Измерение расстояний с помощью масштаба. Нужно прочертить прямую линию (если нужно узнать расстояние по прямой) между двумя точками и с помощью линейки измерить это расстояние в сантиметрах, а затем следует умножить полученное число на величину масштаба. Например, на карте масштаба 1 : 100 000 (в 1 см 1 км) расстояние равно 5 см, т. е. на местности это расстояние составляет 1 * 5 = 5 (км). Измерять расстояние по карте можно и с помощью циркуля-измерителя. В этом случае удобно пользоваться линейным масштабом.
Измерение расстояний с помощью градусной сети. Для расчета расстояний по карте или глобусу можно использовать следующие величины: длина дуги 1° меридиана и 1° экватора равна приблизительно 111 км. Для меридианов это верно всегда, а длина дуги 1° по параллелям уменьшается к полюсам. На экваторе его можно тоже принять равному 111 км. А на полюсах – 0 (т. к. полюс – это точка). Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км. Для определения расстояния между двумя точками на экваторе, также нужно определить расстояние между ними в градусах, а затем умножить на 111 км.
Масштаб. Виды масштабов. Точность масштаба

Рис.2.2 Линейный масштаб
По линейному масштабу расстояния измеряют с точностью 0,0 2-0,03 основания или примерно 0,5мм.
Поперечный масштаб – это график или номограмма, построенный с использованием метода пропорционального клина. Его применяют для измерений и построений на картах с повышенной точностью. Обычно его гравируют на металлических линейках или транспортирах, такие линейки называют масштабными. Он может быть построен и на чертежной бумаге. Поперечный масштаб устроен следующим образом. Он имеет вид прямоугольника, разделенного вертикальными, горизонтальными и наклонными линиями. Нижняя горизонтальная линия разделена на отрезки равные 2см, называемые основаниями масштаба, они пронумерованы: ниже линии оснований масштаба на правом краю первого основания подписан ноль, далее 1, 2, 3 и т.д., на левом краю первого основания – 1. Через концы оснований проведены перпендикуляры, которые разделены на 10 частей горизонтальными линиями с расстояниями между ними 2, 2,5 или 3мм. Нижняя и верхняя линии первого основания разделены на 10 частей. Ноль нижнего основания соединен наклонной линией с первым слева от нулевого перпендикуляра делением верхней линии, первый слева нижний со вторым слева верхним и т.д., 9-й нижний с последним (десятым) верхним. Наклонные линии называют трансверсалями. Таким образом, левая часть графика имеет вид горизонтальных и наклонных линий. Фигуры между нулевым перпендикуляром и первой к нему трансверсалью и первым слева перпендикуляром и ближайшей к нему трансверсалью имеют вид пропорционального клина. Расстояния на горизонтальных линиях между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и трансверсалями изменяется от одной сотой на первой горизонтальной линии до одной десятой доли основания на последней – верхнем основании (рис.1б). Так как первое основание разделено на десять частей и перпендикуляр к нему разделен также на десять частей, то минимальное расстояние между вертикальной и наклонной линиями клина на горизонтальной линии составляет одну сотую долю основания, поэтому такой поперечный масштаб называют сотенным. Поперечный масштаб строят в следующем порядке. На прямой линии, как и при построении линейного масштаба, откладывают несколько раз основание масштаба равное 2см. Основания нумеруют: слева от нуля 1, справа – 1, 2,3 и т.д. В конечных точках основания восстанавливают перпендикуляры длиной, равной основанию, или большей длины. Крайние перпендикуляры делят на десять частей, и через полученные точки проводят
Рис. 2.3. Линейный и поперечный масштабы
прямые линии, параллельные линии оснований. Нижнюю и верхнюю линии первого основания делят на десять равных частей. Полученные точки соединяют следующим образом: нулевую точку нижнего основания с первым верхним слева, первую нижнюю – со второй верхней и т.д. девятую нижнюю с десятой верхней, как показано на рис.1б. С помощью поперечного масштаба можно измерить длину отрезка на плане (карте) с точностью половины наименьшего деления клина, т.е. 0,1мм. Для отложения на плане измеренного на местности расстояния (горизонтального проложения), его выражают в долях основания масштаба (целых и дробных) делением на величину основания в заданном масштабе, наносят на график и с него циркулем переносят на план (карту).
Дата добавления: 2015-03-19 ; просмотров: 16769 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Масштаб карты, виды масштабов.



При составлении планов и карт горизонтальные проекции линий местности уменьшают в определенное число раз в зависимости от требований к точности, предъявляемых к картам (планам).
Масштаб карты— степень уменьшения линии на карте или плане относительно горизонтального проложения соответствующей линии на местности.
При работе с картой, планами или аэрофотоснимками местности пользуются различными масштабами: численным или графическим (линейным, пропорциональным, поперечным).
Определение расстояний с помощью численного масштаба
Численный масштаб — масштаб длин, выраженный отвлеченным числом, в котором числитель — единица, а знаменатель — число, показывающее, во сколько раз уменьшены линейные размеры карты:
где d — длина линии на карте;
М — знаменатель масштаба карты;
D — длина горизонтального проложения этой линии на местности.
Масштаб карты или плана определяет подробность изображения на них элементов местности. Чем больше значение знаменателя численного масштаба М, тем больше степень уменьшения горизонтальных проекций линий местности, тем мельче масштаб плана или карты и менее подробно изображены элементы местности. И наоборот, чем знаменатель М меньше, тем масштаб будет крупнее, тем с большей подробностью и детальностью могут быть показаны на них элементы местности.
Например, численный масштаб 1:50 000 является более мелким, чем масштаб 1:25 000, но более крупным, чем масштаб 1:100 000.
Для удобства знаменатель численного масштаба принимают равным круглому числу: 1:500, 1:1 000, 1:2 000, 1:5 000 и 1:10 000 — для планов, 1:25 000, 1:50 000, 1:100 000, 1:200 000, 1:500 000, 1:1 000 000 — для топографических карт. Указанные отношения показывают, что горизонтальные проекции линий местности уменьшены соответственно в 500, 1000, 2000 раз и т. д., то есть отрезку 1 см на плане соответствуют на местности длины: 500 см или 5 м; 1000 см или 10 м; 2000 см или 20 м и т. д.
Расстояние на местности в метрах или километрах, соответствующее 1 см карты или плана, называется величиной масштаба. Численный масштаб и величина масштаба размещаются под южной стороной рамки листа карты.
Непосредственное использование численного масштаба в практической работе связано с вычислениями, которые необходимы для перехода от горизонтальных проекций линий местности к соответствующим линиям плана или карты, и наоборот.
При пользовании численным масштабом расстояния на карте или плане могут быть измерены в сантиметрах линейкой или курвиметром (см. гл. 2). Полученное при этом число сантиметров умножают на знаменатель масштаба.
Например, линия на карте d = 13,14 см, а масштаб карты 1:100 000. Используя формулу перехода от линий карты (плана) к горизонтальным проекциям соответствующих линий местности D = dM, получим D = 13,14-100 000 =1314 000см = 13 140 м = =13,14 км.
Для нанесения на карту или план линий, измеренных на местности, используют равенство
Например, D = 3750м; 1:М = 1:50 000, тогда d = 3750:50 000 = 0,075м = 7,5 см.
5.1.2. Измерение расстояний с помощью графических масштабов
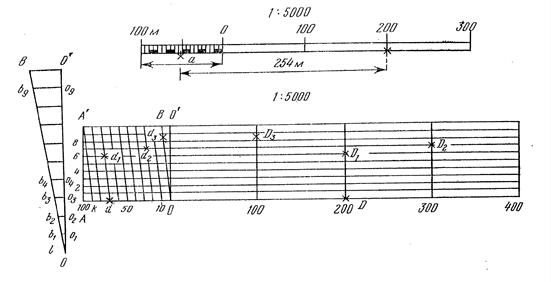
Линейным масштабом называется графическое изображение численного масштаба в виде прямой линии с делениями для отсчета расстояний. Для построения линейного масштаба на прямой линии откладывают ряд отрезков одинаковой длины, называемой основанием линейного масштаба (рис. 5.1). Основание масштаба обычно соответствует целому числу километров или сотен метров.
Для повышения точности измерения первое основание разделено на более мелкие части. Для карты масштаба 1:50 000 (рис. 5.1) наименьшее деление на линейном масштабе будет соответствовать 50 м.
Измерения по линейному масштабу производят циркулем-из- мерителем (рис. 5.2). При измерении циркуль следует держать одной рукой, наклоняя от себя так, чтобы были хорошо видны одновременно обе иглы. И определяя с помощью линейного масштаба длину линии, взятой с карты или плана, нужно правую ножку циркуля поставить на одну из черточек справа от нуля с таким расчетом, чтобы вторая его ножка точно совпала с крайним левым основанием масштаба.
Суммируя отсчеты по правой и левой ножкам циркуля-измерителя, получим искомую длину линии.
Например, на рис. 5.2 искомое расстояние измеренной по карте линии будет соответствовать 1 км 250 м на местности.
При измерении длин больших линейных объектов, когда развод ножек циркуля больше размеров линейного масштаба, имеющегося на карте, в качестве «помощницы» можно использовать километровую сетку. Раствор циркуля-измерителя устанавливают на одну из линий километровой сетки так, чтобы одна из игл попадала на перекрестие сетки. Затем, сокращая раствор циркуля-измерителя, перемещают ее от перекрестия до следующего перекрестия с подсчетом километров до тех размеров, когда можно использовать линейный масштаб карты.
Пропорциональный масштаб — графический масштаб в виде угла, расчлененного системой равноотстоящих параллельных прямых. Он применяется в тех случаях, когда необходимо работать стопографической картой и аэрофотоснимком местности одновременно, в частности при дешифрировании аэрофотоснимков и нанесении объектов с аэрофотоснимка на топографическую карту.
Для повышения точности измерения длин линий на картах (планах) пользуются поперечным масштабом.
Поперечный масштаб представляет собой сочетание линейного и пропорционального масштабов.
Поперечные масштабы изготавливаются на заводах. Они гравируются с помощью делительных машин на специальных металлических линейках, называемых масштабными, а также на линейках топографических приборов.
Поперечный масштаб, основание которого равно 2 см, а остальные деления равны десятым и сотым долям основания, называется нормальным поперечным масштабом (рис. 5.3). Наименьшее деление поперечного масштаба с основанием 2 см равно 0,02 см. Если основание поперечного масштаба взять 1 см, то наименьшее деление его будет равно 0,01 см.
Измерение расстояний с помощью поперечного масштаба начинают с определения цены его делений применительно к заданному численному масштабу, то есть уясняют, сколько километров или метров содержится в целом основании, а также в его десятой и сотой долях.
Каждая линия, откладываемая на плане или карте с помощью поперечного масштаба, слагается из трех частей:
• числа целых оснований, взятых от нулевого перпендикуляра до правой ножки циркуля-измерителя;
• числа малых делений (десятых долей основания), взятых от нулевого перпендикуляра до левой ножки циркуля-измерителя;
• сотых долей основания, расположенных между вертикальной линией и трансверсалью.
Рис. 5.3. Нормальный поперечный масштаб
Аналогично можно решить обратную задачу: по длине отрезка на карте (плане) определить длину соответствующей линии местности.
Устанавливают раствор циркуля на 1000 м так, чтобы левая ножка циркуля-измерителя была на отметке 0 поперечного масштаба, а правая — на отметке 1 (рис. 5.3). Затем передвигают левую ножку циркуля на три малых деления влево, что соответствует 300 м. Оставшиеся 60 м добавляют передвижением ножек циркуля вверх на шесть делений так, чтобы его правая игла скользила по вертикальной линии 1 поперечного масштаба, а левая — по третьей наклонной линии. Требуемый раствор циркуля (1000 + 300 + 60) показан на рис. 5.3.
При пользовании поперечным масштабом необходимо следить, чтобы концы обеих ножек циркуля-измерителя располагались на одной горизонтальной линии масштаба.
Таким же способом можно откладывать с помощью поперечного масштаба отрезки в любом другом масштабе карты.
Например, на рис. 5.3 расстояние, которому соответствует данный раствор циркуля при масштабе карты 1:100 ООО, равно 2720 м (2000 + 600 + 120).
С помощью нормального поперечного масштаба откладывают и измеряют расстояния с точностью до 0,2 мм, что соответствует одной сотой основания. Если же положение ножек циркуля между горизонтальными линиями поперечного масштаба оценивать на глаз, то можно откладывать расстояния с точностью до 0,1 мм.
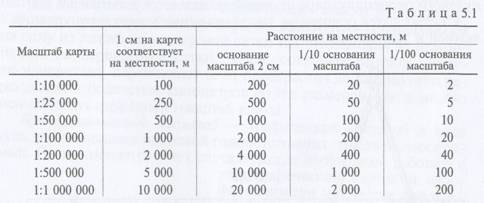
При измерении расстояний по топографическим картам с помощью поперечного масштаба можно пользоваться данными табл. 5.1.
| Масштаб карты | 1:10 000 | 1:25 000 | 1:50 000 | 1:100 000 | 1:200 000 |
| Средняя ошибка, м | 5-10 | 12-25 | 25-50 | 50-100 | 100-200 |
Значения средних ошибок для различных масштабов приведены в табл. 5.2.