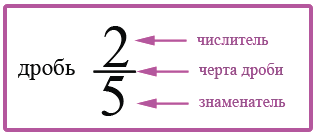Что называют обыкновенной дробью

Дроби обыкновенные правильные и неправильные, смешанные и составные.

Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.

Числитель дроби — число, показывающее количество взятых долей (находится в верхней части дроби – над чертой). Знаменатель дроби — число, показывающее, на сколько долей разделена единица (находится под чертой – в нижней части). Обыкновенные дроби, в свою очередь делятся на: правильные и неправильные, смешанные и составные. Обыкновенные дроби тесно связаны с единицами измерения. 1 метр содержит в себе 100 см. Что означает, что 1 м разделён на 100 равных долей. Таким образом, 1 см = 1/100 м (один сантиметр равен одной сотой метра).

или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:

Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной:

Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному:

Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.

Число, содержащее целую и дробную части, называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью. Тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).

К подобному виду обычно и приводят смешанные дроби.

Составные дроби.

Многоэтажной, или составной дробью является дробь, которая содержит в себе несколько горизонтальных (либо реже — наклонных) черт:

либо либо .

Источник

Какие дроби называются обыкновенными

Что такое обыкновенная дробь — понятие и определение

Прежде чем дать определение термину «дробь», необходимо рассмотреть, чем она является в сущности.

Доля целого или доля числа — это каждая равная часть, которые вместе составляют целый предмет.

К примеру, апельсины обычно состоят из 10 одинаковых долек. А если торт разрезать пополам, то он будет состоять из двух долей.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

У каждой доли свое название, которое зависит от количества долей в предмете.

Половина — это одна вторая часть от целого. Долька апельсина — это одна десятая от апельсина. Если пиццу разрезать на шесть частей, то каждая часть равна одной шестой от всей пиццы.

Простыми словами, дробное число — это нецелое количество, часть целого, которая получается при «дроблении». «Целым» может быть что угодно: количество денег, еда, числа, делимые предметы и так далее.

Как выглядит, примеры записи

Всего существует два вида записи дробных чисел:

Числитель и знаменатель

Обыкновенная дробь состоит из двух натуральных чисел. Записываются они в определенном порядке. Чтобы понять этот принцип, необходимо изучение и объяснение сути дробных чисел.

В сущности, дробь — это результат деления, в котором делимое не делится на делитель полностью, без остатка. Черточка между верхней и нижней части дроби — дробная черта — равноценна знаку деления.

Числитель обыкновенной дроби вида \(\frac mn\) — это натуральное число m, равное делимому.

Знаменатель обыкновенной дроби вида \(\frac mn\) — это натуральное число n, равное делителю.

В зависимости от отношений числителя и знаменателя, выделяют 2 вида дробей.

Правильная дробь — та, у которой числитель меньше знаменателя.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему.

Обычно такие дробные числа записывают в виде целых или смешанных чисел: \(5\frac47, \ 2\frac<14><32>.\)

Знаменатель показывает, из скольких частей состоит предмет. Числитель отображает, сколько таких частей рассматривается в задаче. Например, дробь \(\frac<11><32>\) (читается «одиннадцать тридцать вторых») указывает на то, что предмет состоит из 32 долей, и для рассмотрения взяли 11 из них.

Положительные и отрицательные дроби

Дробные числа бывают не только правильными и неправильными, но также и положительными и отрицательными.

Положительная дробь \(\frac23\) и отрицательная дробь \(-\frac23\) — это противоположные числа.

Положительные дроби можно получить двумя способами:

Отрицательные дроби также получают двумя способами:

Какие действия можно выполнять с обыкновенными дробями

Для выполнения действий с дробными числами необходимо знать их свойства.

Основное свойство дроби — если числитель и знаменатель дроби умножить или разделить на одно и то же число, получится равная ей дробь.

В общем виде это правило записывают так: \(\frac mn=\frac,\)

где a, b, k — натуральные числа.

Основных действий, которые можно выполнять с дробями, несколько.

Если у двух дробей равные знаменатели, то сравнивать необходимо только числители.

У положительных чисел чем больше числитель, тем больше число: \(\frac37>\frac17.\)

У отрицательных чисел чем меньше числитель, тем больше число, т. к. оно ближе к нулю: \(-\frac25>-\frac45.\)

Если знаменатели разные, то дроби необходимо сперва привести к общему знаменателю. Подробнее это действие рассмотрено в других статьях.

В результате сложения обыкновенных дробей получается обыкновенная дробь.

Если знаменатели одинаковые, складывать нужно только числители: \(\frac13+\frac13=\frac23.\)

Если знаменатели разные, дробь необходимо привести к общему знаменателю.

Когда в результате решения получается неправильная дробь, его необходимо привести к виду целого или смешанного числа.

Это действие обратно сложению. Правила действуют те же, что и при сложении: \(\frac7<10>-\frac2<10>=\frac5<10>=\frac12.\)

Результатом умножения двух обыкновенных дробей также всегда является обыкновенная дробь. При этом числитель умножается на числитель, а знаменатель умножается на знаменатель (отсюда следует, что знаменатели могут быть разные): \(\frac23\cdot\frac34=\frac<2\cdot3><3\cdot4>=\frac6<12>=\frac12.\)

Это действие обратно умножению. Чтобы разделить одну дробь на другую, необходимо числитель первой дроби умножить на знаменатель второй, а знаменатель первой — на числитель второй. Иными словами, вторую дробь необходимо «перевернуть» и выполнить умножение:

Источник

Доли. Обыкновенные дроби

Нам известно, что при подсчете чего-либо мы используем натуральные числа, но часто приходится что-то целое делить на части. Например, нам дан апельсин:

Допустим, нам надо разделить апельсин на 6 равных частей:

В этом случае каждую часть называют долей. То есть целый апельсин разделили на 6 частей, поэтому мы можем сказать, что апельсин это 1 целая, и 6 долей апельсина тоже составляет 1 целую:

Название долей зависит от числа частей. Каждая доля в нашем случае будет называться «одной шестой долей апельсина» или, короче, «одной шестой апельсина«. Если апельсин поделить на 8 частей, то мы получим восьмые доли. При этом, чем на большее число частей делят целое, тем меньше доля.

Например, рассмотрим брусок:

Разделим его на 5 частей:

То есть мы получим пятые доли бруска. Закрасим две части красным:

Теперь закрасим три части бруска:

Мы закрасили три пятые доли. Дробь, обозначающая эти доли, записывается так: .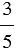

Теперь закрасим желтым цветом пять частей бруска:

Мы закрасили пять пятых долей, то есть мы закрасили весь брусок. Дробь, обозначающая эти доли, записывается так: .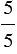

Рассмотрим рисунок ниже:

Определения

Правильная дробь – это дробь, числитель которой меньше знаменателя.

Неправильная дробь – это дробь, у которой числитель больше знаменателя или равен ему.

Поделись с друзьями в социальных сетях:

Источник

Урок 32 Бесплатно Доли. Обыкновенные дроби

Сегодня на уроке мы познакомимся с новым математическим понятием- доли целого (доли числа).

Научимся называть, записывать и сравнивать доли.

Вы узнаете, что такое обыкновенная дробь.

Выясним, что такое знаменатель и числитель дроби, узнаем, что они обозначают.

Рассмотрим правила чтения и записи обыкновенных дробей.

Определим, где на координатном луче располагаются дробные числа.

Не раз вы слышали такие выражения: налить треть стакана молока, отмерить пол чайной ложки соды, четверть часа, полкилограмма сахара и т.д.

Во всех предложенных фразах необходимо найти, определить, отмереть некоторую часть от целого.

Каждому человеку в своей жизни приходилось делить целое на доли, находить часть чего-либо.

Например, резать арбуз, торт, яблоко, делить мандарин, апельсин, плитку шоколадки на дольки и т.д.

Попробуем выяснить, что значит разделить на доли, что такое доля и как ее обозначают.

Представим, что на дне рождении разрезали торт на несколько равных кусков, т.е. разделили его на некоторое количество одинаковых частей.

Неразрезанный торт представлял собой целое.

Каждая равная часть, из которых состоял разрезанный торт, называется долей целого (или просто долей).

Доли- это каждая из равных частей одного целого (единицы).

Целое на доли можно разделить по-разному: можно доли сделать как большими, так и маленькими.

Допустим, две одинаковые пиццы разрезали на части (доли).

Первую пиццу разделили на четыре части, а вторую разрезали на восемь частей.

Понятно, что доли первой пиццы по размеру будут отличаться от долей второй.

Кусочки пиццы, разрезанной на четыре части, будут гораздо больше, чем кусочки пиццы, разделенной на восемь частей.

Чем больше число долей, тем меньше каждая доля.

Следовательно, чем меньше число долей, тем больше каждая доля.

При делении целого на равные части- доли, каждая доля получает свое название, которое указывает на то, какая это часть от целого, и на сколько долей разделено это целое.

Рассмотрим названия долей и каким образом эти названия образуются.

Каждая такая часть будет равна одной второй, записывается это число так: ½ или \(\mathbf<\frac<1><2>>\).

Число под чертой говорит на сколько равных частей разделили целое.

Число под чертой означает сколько таких частей взяли.

Половина- самая известная и часто употребляемая доля.

В жизни часто приходится находить, отмерять, отрезать и т.д. половину чего-либо.

У меня есть дополнительная информация к этой части урока!

В русском языке в составе сложного слова существует приставка «пол-/полу-», которая обозначает половину чего-то.

Приведем несколько примеров.

Уточняя время по часам, мы говорим «полчаса, полминуты», имея ввиду половину часа, половину минуты и т.д.

Полкилометра- расстояние, равное половине одного километра (500 метров).

Полгода (полугодие)- промежуток времени равный половине года (шесть месяцев).

Полкилограмма- единица массы, равная половине килограмма, т.е. 500 граммов.

Полсотни- половина от ста, 100 ÷ 2 = 50.

Каждая такая часть будет равна одной третьей.

Записывается это число так: 1/3 или \(\mathbf<\frac<1><3>>\).

Каждая такая часть будет равна одной четвертой.

Записывается это число так: 1/4 или \(\mathbf<\frac<1><4>>\).

Каждая такая часть будет равна одной пятой.

Записывается это число так: 1/5 или \(\mathbf<\frac<1><5>>\).

Если единицу (целое) разделить на n одинаковых долей, то каждая такая часть будет равна одной n-ой.

Запись 1/n или \(\mathbf<\frac<1>>\) означает, что единицу разделили на n равных частей и взяли одну из них.

Пройти тест и получить оценку можно после входа или регистрации

Обыкновенные дроби

Для описания количества долей используют обыкновенные дроби.

Можно догадаться по смыслу, что слово «дробь» означает дробление чего-либо на части, деление, разделение.

Запись вида \(\mathbf<\frac>\) или m/n называют обыкновенной дробью.

Причем m и n— любые натуральные числа.

В общем говоря, математическая запись обыкновенной дроби оформляется в виде двух чисел, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).

Число, стоящее над дробной чертой (« m ⁄ » или «\(\mathbf<\frac<\color><>>\)»), называют числителем.

Числитель показывает, сколько долей взяли от целого.

Число, стоящее под дробной чертой (« ⁄ n » или «\(\mathbf<\frac<><\color>>\)»), называют знаменателем.

Знаменатель показывает, на сколько всего равных долей разделили целое.

Читают дроби следующим образом: сначала произносят числитель, затем- знаменатель.

При чтении обыкновенных дробей помните, что числитель дроби- количественное числительное (отвечающее на вопрос «сколько долей взято?»), например, шесть, десять, двадцать один и т.д.

Знаменатель- порядковое числительное (отвечает на вопрос: «какая?», «каких?»), например, восьмая, десятая, сотая, шестых, двадцатых и т.д.

В таком случае, если целый торт разделить на 12 частей и съесть 2 кусочка, то запись вида \(\mathbf<\frac<2><12>>\) будет обозначать часть торта, которую съели (из 12 кусочков съели 2).

2 (количество долей, которые взяли)- числитель дроби, он располагается над дробной чертой.

12 (общее количество долей)- знаменатель дроби, стоит под дробной чертой.

Дробь \(\mathbf<\frac<2><12>>\) читают так: «две двенадцатых».

Оставшиеся нетронутые кусочки торта найдем следующим образом:

Следовательно, запись вида \(\mathbf<\frac<10><12>>\) представляет собой часть торта, которая осталась несъеденной (из 12 кусочков 10 не съедены).

10 (количество долей, которые остались)- числитель дроби, он располагается над дробной чертой.

12 (общее количество долей)- знаменатель дроби, стоит под дробной чертой

Дробь \(\mathbf<\frac<10><12>>\) читают так: «десять двенадцатых».

История возникновения обыкновенных дробей.

Первые упоминания дробей, согласно различным историческим исследованиям, были выявлены в глубокой древности у разных народов.

И это естественно, так как всегда существовала потребность делить целое на части, определять размеры полученных частей.

Не всегда удавалось сделать точные вычисления, выразить измеряемые величины натуральными числами, в связи с этим возникала необходимость нахождения частей целого, введения дробных величин.

Значение слова «дробь» имеет арабское происхождение, обозначает «дробить, ломать, разделять».

У разных государств древнего мира были свои представления о дробных числах, о форме их записи, о математических действиях, которые можно совершать с ними.

В Древнем Египте и Вавилоне были первые упоминания о дроби.

Эти два великих древних государства имели различный подход в представлении дробного числа.

Первой известной дробью в истории дробных чисел была «половина»- одна вторая (\(\mathbf<\frac<1><2>>\)), затем появились треть, четверть и т.д.

У меня есть дополнительная информация к этой части урока!

Дроби в Древнем Египте на протяжении долгого времени носили название «ломаные числа».

Использовали Древние Египтяне простые дроби- единичные дроби, числитель которых всегда был равен единице, знаменателем же могло быть любое натуральное число.

При вычислениях все дроби представляли в виде суммы нескольких слагаемых вида \(\mathbf<\frac<1>>\), где n— натуральное число.

Одним из древнейших упоминаний о Египетских дробях считается папирус Ринда.

Папирус включает в себя таблицу дробей и задачи с решениями и ответами.

Египтяне записывали дроби специальными иероглифами.

Они умели выполнять различные математические действия с дробями.

Вычислительные техники и математические навыки в Вавилоне были на более высоком уровне, чем в Древнем Египте.

В этом древнем государстве пользовались шестидесятеричной системой счисления.

В такой системе счисления каждый новый разряд отличался от предыдущего на 60.

Такая система счисления была удобна для измерения углов и времени.

Мы сохранили до сих пор особенности подсчета и определения времени и углов (деление часа и углового градуса на 60 минут, а минут на 60 секунд).

Шестидесятые доли были обычным делом в Вавилоне, соответственно и дроби использовались со знаменателем 60 или степени 60-ти.

Дроби записывались специальными знаками.

Дроби, записанные в шестидесятеричной системе счисления, позже стали использовать астрономы и математики других народов и государств.

Продолжительное время (примерно до XVII века) шестидесятеричные дроби называли астрономическими дробями.

В Древней Греции обыкновенные дроби и действия с ними использовали редко, а если и использовали, то специальной установленной формы записи дробей у них не существовало.

Пользовались они Египетской или Вавилонской формой представления дробей.

В целом Греки редко применяли дроби в своей математике, основывая свои умозаключения и вычисления в основном на понятии целого числа.

Однако, древнегреческий ученый и философ Пифагор и его последователи допускали существование дроби как отношение двух целых чисел, но единицу они считали неделимой.

Пифагор и его ученики умели производить математические операции над дробями, а также сравнивать дробные числа.

История возникновения дроби в Римской империи связана с мерой массы, которая носила название «асс».

Асс делился на 12 долей, каждая такая доля называлась «унция».

Из таких долей образовывались дроби со знаменателем 12.

Таким образом возникли Римские двенадцатеричные дроби, знаменатель которых всегда был равным 12.

У Римлян дробь \(\mathbf<\frac<1><12>>\)- это одна унция.

Три унции- это четверть.

Четыре унции называли треть.

Шесть унций считали «половиной».

В других древних государствах так же существовало понятие о дробях и о возможных математических операциях с ними.

В математике Древнего Китая уже во втором веке до н.э. существовало понятие дробь числа, они умели сокращать дроби и выполнять различные арифметические операции с ними.

В научных трудах древнеиндийского математика Брахмагупты встречаются различные дроби как основные (числитель таких дробей является единицей), так и производные (числителем в таких дробях является любое число).

Дробь в его записях имеет двухэтажную форму (похожа на современную дробь): числитель расположен в верху, а знаменатель- под ним внизу, но горизонтальная черта- дробная черта в его записях отсутствует.

В России первое упоминание о дробях было в начале двенадцатого века в трудах русского средневекового новгородского мыслителя, математика, священнослужителя и летописца Кирика, он время делил на мелкие доли, выяснял сколько дробных часов содержится в одном дне.

До семнадцатого века на Руси дроби называли долями, в начале восемнадцатого века дроби стали называть «ломаными числами», дроби имели названия: полтина (половина), четь, треть, пятина, десятина и др.

Со временем менялась форма записи дробей, усложнялись математические операции, производимые с ними.

Впервые дробную черту, разделяющую числитель и знаменатель, стали применять в своих трудах арабы.

Первым европейским математиком, который применил дробную черту в своем научном труде (1202 год.), был итальянский путешественник, купец Леонардо Пизанский.

Дробная черта стала признанной лишь в шестнадцатом веке.

Термины «числитель» и «знаменатель» ввел греческий монах, ученый, математик Максим Плануд в тринадцатом веке

Обыкновенную дробь можно изобразить на координатном луче.

Известно, что любому числу координатного луча соответствует одна единственная точка.

Следовательно, любому дробному числу соответствует конкретное место на координатном луче.

Чтобы обозначить на координатном луче точку с координатой \(\mathbf<\frac>\), необходимо от начала координат отложить m отрезков, длина каждого такого отрезка должна составлять \(\mathbf<\frac<1>>\) от единичного отрезка.

Чтобы найти число \(\mathbf<\frac<1>>\), нужно единичный отрезок разделить на n равных частей.

Рассмотрим поясняющий пример.

Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком 1 деление = 1 единица.

Отметим на координатном луче точку А(\(\mathbf<\frac<4><6>>\)).

Дробь \(\mathbf<\frac<4><6>>\) говорит о том, что из шести долей единичного отрезка взяли четыре.

Единичный отрезок разобьем на 6 равных частей, равных \(\mathbf<\frac<1><6>>\).

Следовательно, точка А(\(\mathbf<\frac<4><6>>\)) удалена от начала координат О(0) на расстояние четырех таких отрезков.

Пройти тест и получить оценку можно после входа или регистрации

Источник