Что называют областью определения уравнения f x g x
Область определения функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Готовимся к ЕГЭ по математике. Использование области определения функций и множества значений функций для решения уравнений
Готовимся к ЕГЭ по математике.
Использование области определения функций и множества значений функций для решения уравнений.
Рассмотрим метод решения уравнений вида f(х)=g(х), основанный на использовании областей определения функций. Этот метод наиболее результативен при решении уравнений, в состав которых входят функции с ограниченной областью определения, как у=аrccоs х, у=arcsin x, у=logaх, у= 
Пусть дано уравнение f(х)=g(х). Если области определения функций у=f (х), у=g(х) не имеют общих значений, то уравнение f(х)=g(х) решений не имеет.
Решить уравнение 
Пусть f(х)= 
g(х)= 
Найдём область определения каждой введённой функции:
Так как области определения общих точек не имеют, то уравнение решений не
Пусть дано уравнение f(х)=g (х). Если области определения функций у=f (х), у=g(х) имеют общее значение (число а), то, если уравнение f(х)=g(х) и имеет решение, то им может быть только число а.
Решить уравнение arcсos х=
f(х)= arcсos х ; g(х)= 
D(f) 
Число 1 может являться корнем уравнения.
Проверка: arcсos1= 
3
f(x)=
g(x)=
Найдем область определения f(х).
(х-9)(х+9)
D(f)=
Найдем область определения g(x).
(х-8)(х+9)
D(f)
Проверим является ли 
Ответ: 
Заметим, что если пересечением областей определения функций является конечное число значений, то необходимо каждое из значений подставить в исходное уравнение и проверить является ли оно корнем.
Характерной особенностью, побуждающей использовать описываемый метод, является наличие в одном уравнении функций различной природы: квадратичной, тригонометрической, показательной и т. п., что затрудняет или делает невозможным использование стандартных методов.
Пусть дано уравнение f(х)=g(х).
Е(f)- множество значений функции f(х) и Е(g)- множество значений функции
g(х). Если пересечением множеств значений функций является число а, то есть
Е(f) ∩Е(g)=a, то уравнение равносильно системе уравнений :

sin
Решение:
f(х)= sin
g(х)=
Удобно решить второе уравнение системы х=2. Подставив число 2 в первое уравнение системы, убеждаемся, что оно верно. Таким образом, 2 является решением системы, а значит и корнем исходного уравнения.
Заметим, если множества значений функций не имеют общих точек, то рассматриваемое в утверждении уравнение решений не имеет.

f (х)= 

Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №1. Область определения и множество значений тригонометрических функций.
Перечень вопросов, рассматриваемых в теме
Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy.
Найдите область определения функции и множество значений функции:
1) 


D(f): 1) 

E(f): 1)


Объяснение нового материала
С помощью единичной окружности сделайте выводы об области определения и множестве значений тригонометрических функций.
Область определения функции
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Используя это определение, охарактеризуем нужное нам понятие более четко:
Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Как найти области определения для основных элементарных функций
Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y = x 2 и т.д., а их области определения указываются в качестве основных свойств.
В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.
Область определения постоянной функции
Область определения функции с корнем
Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.
Область определения степенной функции
Перечислим возможные варианты.
Поясним нашу мысль несколькими примерами.
Область определения показательной функции
Область определения логарифмической функции
Область определения тригонометрических функций
Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.
Область определения тригонометрических функций
К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.
Области определения основных функций в табличном виде
Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.



































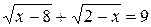
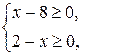 то есть
то есть 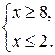
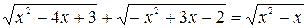
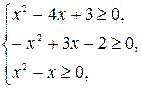
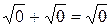 — верное числовое равенство. Значит, число 1 — корень данного уравнения.
— верное числовое равенство. Значит, число 1 — корень данного уравнения.