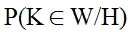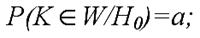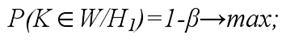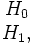Что называют мощностью критерия
Проверка статистических гипотез
Материал из MachineLearning.
Содержание
Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.
Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.
Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.
Методика проверки статистических гипотез
Методика состоит в следующем.
Замечание. Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна. Тому есть две причины.
Альтернативная методика на основе достигаемого уровня значимости
Широкое распространение методики фиксированного уровня значимости было вызвано сложностью вычисления многих статистических критериев в докомпьютерную эпоху. Чаще всего использовались таблицы, в которых для некоторых априорных уровней значимости были выписаны критические значения. В настоящее время результаты проверки гипотез чаще представляют с помощью достигаемого уровня значимости.
Достигаемый уровень значимости (пи-величина, англ. p-value) — это наименьшая величина уровня значимости, при которой нулевая гипотеза отвергается для данного значения статистики критерия
где — критическая область критерия.
Другая интерпретация: достигаемый уровень значимости — это вероятность при справедливости нулевой гипотезы получить значение статистики, такое же или ещё более экстремальное, чем
Если достигаемый уровень значимости достаточно мал (близок к нулю), то нулевая гипотеза отвергается. В частности, его можно сравнивать с фиксированным уровнем значимости; тогда альтернативная методика будет эквивалентна классической.
Типы критической области
На практике, как правило, используются статистики с унимодальной (имеющей форму пика) плотностью распределения. Критические области (наименее вероятные значения статистики) соответствуют «хвостам» этого распределения. Поэтому чаще всего возникают критические области одного из трёх типов:
Ошибки первого и второго рода
Свойства статистических критериев
Типы статистических гипотез
Типы статистических критериев
В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.
Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.
Критерии согласия
Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.
Критерии сдвига
Специальный случай двухвыборочных критериев согласия. Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.
Критерии нормальности
Критерии нормальности — это выделенный частный случай критериев согласия. Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел. Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии. Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические. В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.
Критерии однородности
Критерии однородности предназначены для проверки нулевой гипотезы о том, что две выборки (или несколько) взяты из одного распределения, либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.
Критерии симметричности
Критерии симметричности позволяют проверить симметричность распределения.
Критерии тренда, стационарности и случайности
Критерии тренда и случайности предназначены для проверки нулевой гипотезы об отсутствии зависимости между выборочными данными и номером наблюдения в выборке. Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны 
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия | H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) | H0 верно отвергнута | |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Правосторонняя критическая область. Левосторонняя и двусторонняя критические области. Мощность критерия
При проверке статистических гипотез используют правосторонние, левосторонние и двусторонние критические области.
Правосторонняя критическая область характеризуется неравенством вида:
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр, – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия.
Следовательно, для определения правосторонней критической области необходимо рассчитать положительное значение статистического критерия lкр.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет больше значения lкр, равна заданному уровню значимости, т.е. P(L>lкр)=a.
Для каждого статистического критерия рассчитаны специальные таблицы, с помощью которых определяют критическую точку, удовлетворяющую заданному уровню значимости.
Левосторонняя критическая область характеризуется неравенством вида:
где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;
lкр, — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия.
Следовательно, для определения левосторонней критической области необходимо найти рассчитать отрицательное значение статистического критерия lкр.
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет меньше значения lкр, равна заданному уровню значимости, т.е. P(L
Двусторонняя критическая область характеризуется двумя неравенствами вида:
Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, сумма вероятностей того, что значение статистического критерия L будет больше значения lкр1 или меньше значения lкр2, равна заданному уровню значимости, т.е. P(L>lкр1)+(L ;
2) левосторонняя критическая область выбирается в том случае, если Н1:‹;
3) двусторонняя критическая область выбирается в том случае, если Н1:≠.
Предположим, что заданы следующие параметры:
1) статистический критерий L;
2) критическая область W, где H0 отклоняется;
3) область принятия гипотезы 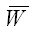
4) вероятность совершить ошибку первого рода a;
5) вероятность совершить ошибку второго рода β.
Тогда справедливо утверждение о том, что выражение
является вероятностью того, что статистический критерий L попадёт в критическую область, если верна гипотеза H.
При построении критической области учитываются два требования:
1) вероятность того, что статистический критерий L попадёт в критическую область, если верна Н0, равна а:
данное равенство задаёт вероятность совершения ошибки первого рода;
2) вероятность того, что статистический критерий L попадёт в критическую область (область отклонения гипотезы Н0 в пользу гипотезы Н1), если верна гипотеза Н1:
данное равенство задаёт вероятность принятия правильной гипотезы.
Мощностью статистического критерия называется вероятность попадания данного критерия в критическую область, при условии, что справедлива конкурирующая гипотеза Н1, т. е.выражение 1-β является мощностью критерия.
Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования обеспечивает минимальную ошибку второго рода, состоящую в том, что будет принята неправильная гипотеза.
Мощность критерия
Ошибки первого рода (англ. type I errors, α errors, false positives ) и ошибки второго рода (англ. type II errors, β errors, false negatives ) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
Определения
Пусть дана выборка 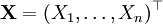
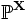
где H0 — нулевая гипотеза, а H1 — альтернативная гипотеза. Предположим, что задан статистический критерий
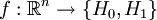
сопоставляющий каждой реализации выборки 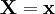
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия | H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) | H0 верно отвергнута | |
О смысле ошибок первого и второго рода
Ниже, в разделе Примеры использования, подробно рассматривается применение понятий ошибок первого и второго рода в различных областях.
Вероятности ошибок (уровень значимости и мощность)
Для проверки статистических гипотез используют так называемые критерии согласия. Для них вероятности ошибок первого и второго рода играют значительную роль.
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «анти-спам» алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда анти-спам система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности анти-спам алгоритма.
Вредоносное программное обеспечение
Понятие ошибки первого рода также ипользуется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с анти-троянскими и анти-
Поиск в компьютерных базах данных
При поиске в базе данных, к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако, это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как террориста) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т. д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т. п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении. [1]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии. [2]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15 %, это самый высокий показатель в мире. [3] Самый низкий уровень наблюдается в Нидерландах, 1 %. [4]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70 %, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными. [5]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиа-свидетельство» (изображение, видеозапись, аудиозапись и т. д.), которое имеет обычное объяснение. [6]