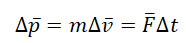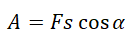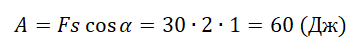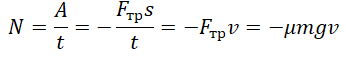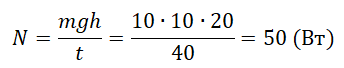Что называют механической работой

Механическая работа и мощность

теория по физике 🧲 законы сохранения

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

Важно!

Механическая работа совершается, если:

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Модуль силы тяжести: F_тяж = mg

Работа силы тяжести: A = mgs cosα

Модуль силы трения скольжения: F_тр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα

Модуль силы упругости: F_упр = kx

Работа силы упругости:

Работа силы тяжести

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела

Работа при равномерном прямолинейном движении определяется формулой:

F_т — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза

Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении

Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали

Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

Наклонная плоскость

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

Источник

Общее определение работы. Механическая работа.

Когда на тело действует постоянна сила и тело совершает в направлении действия силы перемещения , то в этом случае производится работа, равная произведению модулей силы и перемещения:

Единицей работы является джоуль (Дж). В СИ за единицу работы принимается работа силы в 1 Н при перемещении точки ее приложения на 1 м:

На тело часто действует несколько сил, а не одна. Например, при перемещении стола по полу на стол действует мускульная сила, с которой толкают или тянут стол, и сила трения скольжения, которая направлена противоположно движению стола.

Если векторная сумма сил, приложенных к телу, равна нулю, то и суммарная работа всех сил, приложенных к телу, должна быть равна нулю.

Значит, силы, направленные против перемещения, также совершают работу со знаком, противоположным знаку работы, совершаемой силой, направленной по движению тела. То есть, работа может быть как положительной, так и отрицательной.

Работа считается положительной, если направление силы и направление перемещения совпадают. Если направление силы противоположно перемещению тела, работа считается отрицательной.

Однако, направление силы может и не совпадать с направлением перемещения. Например, сани движутся по горизонтальной поверхности, а сила, приложенная к ним, направлена под углом α к горизонту. Чтобы вычислить работу, силу представим как сумму двух сил: и . Поскольку в вертикальном направлении перемещение санок равно нулю, то работа силы равна нулю. Следовательно, работа силы равна работе силы :

Поскольку , то

Работа, совершаемая постоянной силой, равна произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы и перемещения.

Из формулы видно, что работа – скалярная величина.

Если угол α тупой, то примет отрицательное значение, это значит, что работа, совершаемая такой силой, отрицательная.

Источник

Что называют механической работой и какие условия её совершения?

Содержание:

Ещё в древности замечена связь между силой, прикладываемой для проделывания работы, и расстоянием, на которое под её действием перемещается тело. Она зависит от направления и точки прикладываемой силы. Рассмотрим, что называют механической работой, какие величины на неё влияют.

Работа постоянной силы

Представьте пару ситуаций: вы:

В обоих случаях вы выполняете работу, прилагаете определённые физические усилия. Что общего между ситуациями? Затрата энергии, прикладывание силы к ранцу для его передвижения – это механическая работа, которую вычисляют по формуле:

Работа связана с модулями изначальной и конечной скоростей, показывает, насколько приложенная сила изменила скорость тела.

, где: v и v₀ – начальная и конечная скорости перемещения материального объекта соответственно.

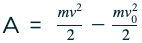
Существует понятие работы силы тяжести, выполняемой при перемещении предмета:

Сила тяготения принимается за ma при небольших расстояниях, а дистанция равняется разнице между начальной и конечной высотой размещения тела.

Примеры, условия совершения механической работы

Запомните: тело совершает механическую работу только тогда, когда оно передвигается под действом приложенной силы. Примеры механической работы в жизни: перемещение вещей руками, транспортом или посредством иных приспособлений: переноска книг, перестановка мебели, если та движется, написание текста, перевозка грузов автомобилем.

Если тело передвигается по инерции, сила равна нулю со всеми вытекающими, как в случае, когда отец пытается передвинуть шкаф, толкнуть автомобиль, которые остаются на месте. Остальные примеры придумайте сами, исходя из личного опыта.

С точки зрения механики интересен момент с Атлантом. Он держит на своих плечах небесный свод, расходуя при этом колоссальную энергию. Небосвод при этом не перемещается – s = 0, а значит, работа не выполняется. Ассоциация проста: Атланта можно заменить массивными колоннами.

​ Аналогичная ситуация возникает, когда вы стоите с полным ранцем школьных принадлежностей на остановке. Вы устаёте, тратите энергию на поддержание тяжести, но работу, по представлениям классической физики, не выполняете. Такая интересная механика.

Источник

Механическая работа. Мощность

1. Механическая работа ​ \( A \) ​ — физическая величина, равная произведению вектора силы, действующей на тело, и вектора его перемещения: ​ \( A=\vec\vec \) ​. Работа — скалярная величина, характеризуется числовым значением и единицей.

За единицу работы принимают 1 джоуль (1 Дж). Это такая работа, которую совершает сила 1 Н на пути 1 м.

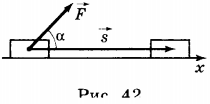
2. Если сила, действующая на тело, составляет некоторый угол ​ \( \alpha \) ​ с перемещением, то проекция силы ​ \( F \) ​ на ось X равна ​ \( F_x \) ​ (рис. 42).

Таким образом, работа постоянной силы равна произведению модулей векторов силы и перемещения и косинуса угла между этими векторами.

3. Если сила ​ \( F \) ​ = 0 или перемещение ​ \( S \) ​ = 0, то механическая работа равна нулю ​ \( A \) ​ = 0. Работа равна нулю, если вектор силы перпендикулярен вектору перемещения, т.е. ​ \( \cos90^\circ \) ​ = 0. Так, нулю равна работа силы, сообщающей телу центростремительное ускорение при его равномерном движении по окружности, так как эта сила перпендикулярна направлению движения тела в любой точке траектории.

5. При свободном падении с высоты ​ \( h \) ​ тело массой ​ \( m \) ​ перемещается из положения 1 в положение 2 (рис. 43). При этом сила тяжести совершает работу, равную:

​

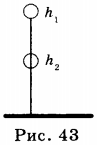
​При движении тела вертикально вниз сила и перемещение направлены в одну сторону, и сила тяжести совершает положительную работу.

Если тело поднимается вверх, то сила тяжести направлена вниз, а перемещение вверх, то сила тяжести совершает отрицательную работу, т.е.

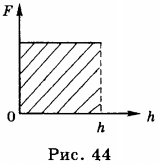
6. Работу можно представить графически. На рисунке изображён график зависимости силы тяжести от высоты тела относительно поверхности Земли (рис. 44). Графически работа силы тяжести равна площади фигуры (прямоугольника), ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс
в точке ​ \( h \) ​.

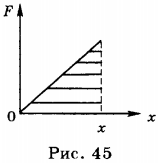
Графиком зависимости силы упругости от удлинения пружины является прямая, проходящая через начало координат (рис. 45). По аналогии с работой силы тяжести работа силы упругости равна площади треугольника, ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс в точке ​ \( x \) ​.
​ \( A=Fx/2=kx\cdot x/2 \) ​.

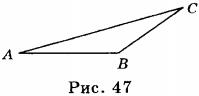
7. Работа силы тяжести не зависит от формы траектории, по которой перемещается тело; она зависит от начального и конечного положений тела. Пусть тело сначала перемещается из точки А в точку В по траектории АВ (рис. 46). Работа силы тяжести в этом случае

Работа силы упругости также не зависит от формы траектории.

Предположим, что тело перемещается из точки А в точку В по траектории АСВ, а затем из точки В в точку А по траектории ВА. При движении по траектории АСВ сила тяжести совершает положительную работу, при движении по траектории В А работа силы тяжести отрицательна, равная по модулю работе при движении по траектории АСВ. Следовательно работа силы тяжести по замкнутой траектории равна нулю. То же относится и к работе силы упругости.

Силы, работа которых не зависит от формы траектории и по замкнутой траектории равна нулю, называют консервативными. К консервативным силам относятся сила тяжести и сила упругости.

Следовательно, работа ​ \( A_ \) ​ не равна работе ​ \( A_ \) ​.

9. Мощностью называется физическая величина, равная отношению работы к промежутку времени, за который она совершена. Мощность характеризует быстроту совершения работы.

Мощность обозначается буквой ​ \( N \) ​.

Единица мощности: ​ \( [N]=[A]/[t] \) ​. ​ \( [N] \) ​ = 1 Дж/1 с = 1 Дж/с. Эта единица называется ватт (Вт). Один ватт — такая мощность, при которой работа 1 Дж совершается за 1 с.

10. Мощность, развиваемая двигателем, равна: ​ \( N = A/t \) ​, ​ \( A=F\cdot S \) ​, откуда ​ \( N=FS/t \) ​. Отношение перемещения ко времени представляет собой скорость движения: ​ \( S/t = v \) ​. Откуда ​ \( N = Fv \) ​.

Из полученной формулы видно, что при постоянной силе сопротивления скорость движения прямо пропорциональна мощности двигателя.

В различных машинах и механизмах происходит преобразование механической энергии. За счёт энергии при её преобразовании совершается работа. При этом на совершение полезной работы расходуется только часть энергии. Некоторая часть энергии тратится на совершение работы против сил трения. Таким образом, любая машина характеризуется величиной, показывающей, какая часть передаваемой ей энергии используется полезно. Эта величина называется коэффициентом полезного действия (КПД).

Коэффициентом полезного действия называют величину, равную отношению полезной работы ​ \( (A_п) \) ​ ко всей совершённой работе \( (A_с) \) : ​ \( \eta=A_п/A_с \) ​. Выражают КПД в процентах.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Работа определяется по формуле

1) ​ \( A=Fv \) ​
2) \( A=N/t \) ​
3) \( A=mv \) ​
4) \( A=FS \) ​

2. Груз равномерно поднимают вертикально вверх за привязанную к нему верёвку. Работа силы тяжести в этом случае

1) равна нулю
2) положительная
3) отрицательная
4) больше работы силы упругости

3. Ящик тянут за привязанную к нему верёвку, составляющую угол 60° с горизонтом, прикладывая силу 30 Н. Какова работа этой силы, если модуль перемещения равен 10 м?

1) 300 Дж
2) 150 Дж
3) 3 Дж
4) 1,5 Дж

4. Искусственный спутник Земли, масса которого равна ​ \( m \) ​, равномерно движется по круговой орбите радиусом ​ \( R \) ​. Работа, совершаемая силой тяжести за время, равное периоду обращения, равна

1) ​ \( mgR \) ​
2) ​ \( \pi mgR \) ​
3) \( 2\pi mgR \) ​
4) ​ \( 0 \) ​

5. Автомобиль массой 1,2 т проехал 800 м по горизонтальной дороге. Какая работа была совершена при этом силой трения, если коэффициент трения 0,1?

6. Пружину жёсткостью 200 Н/м растянули на 5 см. Какую работу совершит сила упругости при возвращении пружины в состояние равновесия?

1) 0,25 Дж
2) 5 Дж
3) 250 Дж
4) 500 Дж

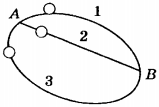
7. Шарики одинаковой массы скатываются с горки по трём разным желобам, как показано на рисунке. В каком случае работа силы тяжести будет наибольшей?

1) 1
2) 2
3) 3
4) работа во всех случаях одинакова

8. Работа по замкнутой траектории равна нулю

А. Силы трения
Б. Силы упругости

Верным является ответ

1) и А, и Б
2) только А
3) только Б
4) ни А, ни Б

9. Единицей мощности в СИ является

10. Чему равна полезная работа, если совершённая работа составляет 1000 Дж, а КПД двигателя 40 %?

1) 40000 Дж
2) 1000 Дж
3) 400 Дж
4) 25 Дж

11. Установите соответствие между работой силы (в левом столбце таблицы) и знаком работы (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами.

РАБОТА СИЛЫ
A. Работа силы упругости при растяжении пружины
Б. Работа силы трения
B. Работа силы тяжести при падении тела

ЗНАК РАБОТЫ
1) положительная
2) отрицательная
3) равна нулю

12. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.

1) Работа силы тяжести не зависит от формы траектории.
2) Работа совершается при любом перемещении тела.
3) Работа силы трения скольжения всегда отрицательна.
4) Работа силы упругости по замкнутому контуру не равна нулю.
5) Работа силы трения не зависит от формы траектории.

Часть 2

13. Лебёдка равномерно поднимает груз массой 300 кг на высоту 3 м за 10 с. Какова мощность лебёдки?

Источник

Механическая работа

Обычно словом «работа» мы называем действие человека или технического устройства. Например, мы говорим: работает плотник, работает холодильник, работает компьютер. В физике термин «работа» имеет более конкретный (определённый) смысл. Поясним это на нескольких примерах действия сил. Взгляните на рисунок.

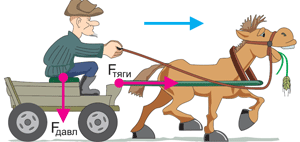Лошадь тянет телегу с некоторой силой, обозначим её Fтяги. Дедушка, сидящий на телеге, давит на неё с некоторой силой. Обозначим её Fдавл. Телега движется вдоль направления силы тяги лошади (вправо), а в направлении силы давления дедушки (вниз) телега не перемещается. Поэтому в физике говорят, что Fтяги совершает работу над телегой, а Fдавл не совершает работу над телегой.

Итак, работа силы над телом или механическая работа – физическая величина, модуль которой равен произведению силы на путь, пройденный телом вдоль направления действия этой силы:

A = ± ( F||· l )

A – механическая работа над телом, Дж F|| – сила, параллельная пути тела, Н l – пройденный телом путь, м

В честь английского учёного Д.Джоуля единица механической работы получила название 1 джоуль (согласно формуле, 1 Дж = 1 Н·м).

Если на рассматриваемое тело действует некоторая сила, значит, на него действует некоторое тело. Поэтому работа силы над телом и работа тела над телом – полные синонимы. Однако, работа первого тела над вторым и работа второго тела над первым – частичные синонимы, поскольку модули этих работ всегда равны, а их знаки всегда противоположны. Именно поэтому в формуле присутствует знак «±». Обсудим знаки работы более подробно.

Числовые значения силы и пути – всегда неотрицательные величины. В отличие от них механическая работа может иметь как положительный, так и отрицательный знаки. Если направление силы совпадает с направлением движения тела, то работу силы считают положительной. Если направление силы противоположно направлению движения тела, работу силы считают отрицательной (берём «–» из «±» формулы). Если направление движения тела перпендикулярно направлению действия силы, то такая сила работу не совершает, то есть A = 0.

Рассмотрите три иллюстрации по трём аспектам механической работы.

Совершение силой работы может выглядеть по-разному с точек зрения различных наблюдателей. Рассмотрим пример: девочка едет в лифте вверх. Совершает ли она механическую работу? Девочка может совершать работу только над теми телами, на которые действует силой. Такое тело лишь одно – кабина лифта, так как девочка давит на её пол своим весом. Теперь надо выяснить, проходит ли кабина некоторый путь. Рассмотрим два варианта: с неподвижным и движущимся наблюдателем.

Пусть сначала мальчик-наблюдатель сидит на земле. По отношению к нему кабина лифта движется вверх и проходит некоторый путь. Вес девочки направлен в противоположную сторону – вниз, следовательно, девочка совершает над кабиной отрицательную механическую работу: Aдев Опубликовано в разделах: 7 класс, Работа и энергия

Источник