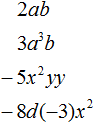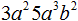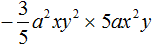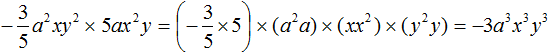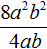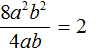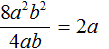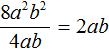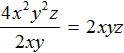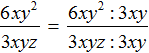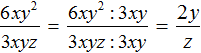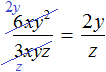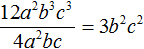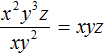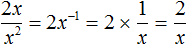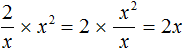Что называют коэффициентом одночлена

Определение одночлена, сопутствующие понятия, примеры.

Одним из видов выражений курса алгебры являются одночлены. В этой статье мы разберемся, какие выражения называют одночленами, скажем про их стандартный вид и приведем примеры. А после этого подробно остановимся на сопутствующих понятиях – степени и коэффициенте одночлена.

Навигация по странице.

Что такое одночлен? Определение, примеры

Первое запланированное знакомство с одночленами происходит в 7 классе средней школы. Там дается следующее определение одночлена:

Одночлены – это числа, переменные, их степени с натуральным показателем, а также всевозможные составленные из них произведения.

До 7 класса в школе были изучены натуральные, целые и рациональные числа, они и фигурируют в приведенных выше примерах одночленов. Однако нужно заметить, что определение одночлена в указанной формулировке остается в силе после знакомства с действительными числами и комплексными числами. Так , 2·π·x 3 и — это тоже одночлены.

Стандартный вид одночлена

С одночленами удобно работать, когда они приведены к так называемому стандартному виду.

Любой одночлен путем тождественных преобразований может быть представлен в стандартном виде. Иными словами, можно любой одночлен привести к стандартному виду.

Степень одночлена

Для одночлена существует понятие его степени. Разберемся, что это такое.

Степень одночлена стандартного вида – это сумма показателей степеней всех переменных, входящих в его запись; если в записи одночлена нет переменных, и он отличен от нуля, то его степень считается равной нулю; число нуль считается одночленом, степень которого не определена.

Коэффициент одночлена

Одночлен в стандартном виде, имеющий в своей записи хотя бы одну переменную, представляет собой произведение с единственным числовым множителем – числовым коэффициентом. Этот коэффициент называют коэффициентом одночлена. Оформим приведенные рассуждения в виде определения.

Коэффициент одночлена – это числовой множитель одночлена, записанного в стандартном виде.

Источник

Одночлен и его стандартный вид

теория по математике 📈 алгебраические выражения

Одночлен – это простейшее алгебраическое выражение, которое состоит из произведения чисел, переменных и их степеней. Никаких других действий одночлен не имеет. Числовой множитель у одночлена называется коэффициентом.

Пример №1. Рассмотрим примеры одночленов.

Стандартный вид одночлена

Чтобы определить коэффициент у одночлена, он должен быть представлен в стандартном виде.

Что такое одночлен стандартного вида?

Одночлен стандартного вида – это одночлен, у которого на первом месте стоит коэффициент, а далее – буквенные множители (переменные).

Такие одночлены приведены в примере №1. Рассмотрим, как привести одночлен к стандартному виду.

Здесь выполняем умножение чисел 3 и (-2), затем степеней х и у (при умножении степеней с одинаковым основанием показатели складываем, а основание оставляем тем же); записываем на первом месте число (коэффициент одночлена), а затем уже степени. Получаем одночлен стандартного вида.

-12a 3 b 2 (-4b 7 )=48a 3 b 9

Данный ответ получен после умножения чисел и степеней с одинаковым основанием. Записан на первом месте коэффициент 48, а затем остальные множители.

Степень одночлена

Сумму показателей степени переменных называют степенью одночлена.

Рассмотрим, как найти степень одночлена.

– 113с 3 х 6

У переменных показатели степени равны 3 и 6, складываем их и получаем 9. Значит, степень одночлена равна 9. Пример №5.

18ху

У этого одночлена степень равна 2, так как у переменных х и у первая степень, складывая 1 и 1, получаем 2.

Источник

Коэффициент одночлена

Что такое коэффициент одночлена? Всегда ли пишут коэффициент?

Коэффициентом одночлена, записанного в стандартном виде, называется его числовой множитель.

Другими словами, коэффициент одночлена — это число, стоящее перед буквенной частью в произведении после приведения одночлена к стандартному виду.

коэффициент равен 4;

Если одночлен состоит только из числового множителя, то этот множитель и есть коэффициент. Например, в одночлене

коэффициент равен 12.

Если в произведении перед буквенной частью не записан числовой множитель, значит, коэффициент одночлена равен единице:

Если одночлен записан не в стандартном виде, прежде чем находить коэффициент, нужно привести его к одночлену стандартного вида.

Источник

Понятие одночлена. Стандартный вид, коэффициент, степень

Содержание

Одночлен – одно из основополагающих понятий в алгебре. Данный урок поможет вам разобраться с его определением, а также со стандартным видом одночлена, степенью и коэффициентом.

Что такое одночлен

$$-5,5y^<12>\times 84b\times 302$$ То есть, в одночлен могут входить как несколько множителей, так и одно число или переменная.

Таким образом, запомним определение:

Числа, переменные, их степени с натуральным показателем, а также различные виды произведений, составленные из этих переменных, чисел и степеней, называют одночленами.

$$\frac<5^9>$$ Иными словами, выражения, содержащие сумму, разность или переменную в знаменателе дроби, одночленами являться не будут.

Стандартный вид одночлена

Для удобства математических вычислений одночлен принято приводить к стандартному виду. Разберемся, что это значит.

Стандартный вид одночлена подразумевает его запись с соблюдением нескольких правил:

Коэффициент

Коэффициентом одночлена называют числовой множитель одночлена, который записан в стандартном виде.

Заметим, что после тождественных преобразований можно привести к стандартному виду абсолютно любой одночлен.

Пример

Степень одночлена

Таким образом, запомним:

Степенью одночлена, записанного в стандартном виде, будет сумма показателей степеней всех переменных, которые в него входят.

Источник

Одночлены

Определения и примеры

Приведём ещё примеры одночленов:

Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 5 2 является одночленом.

Приведение одночлена к стандартному виду

Рассмотрим следующий одночлен:

Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.

Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.

Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.

Итак, приведём одночлен 3a 2 5a 3 b 2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:

Мы привели одночлен 3a 2 5a 3 b 2 к стандартному виду. В результате получили одночлен 15a 5 b 2

Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.

Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc

Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.

Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.

Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.

Пример 1. Привести одночлен 5xx3ya 2 к стандартному виду

Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:

Пример 2. Привести одночлен 2m 3 n × 0,4mn к стандартному виду

Перемножим числа, переменные и степени по отдельности.

Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m 3 × m и n × n

Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:

Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.

Сложение и вычитание одночленов

Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.

Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.

Пример 1. Сложить одночлены 6a 2 b и 2a 2 b

Сложим коэффициенты 6 и 2, а буквенную часть 6a 2 b оставим без изменений

Пример 2. Вычесть из одночлена 5a 2 b 3 одночлен 2a 2 b 3

Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:

Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:

Умножение одночленов

Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.

Пример 1. Перемножить одночлены 5x и 8y

Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:

Пример 2. Перемножить одночлены 5x 2 y 3 и 7x 3 y 2 c

Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:

Пример 3. Перемножить одночлены −5a 2 bc и 2a 2 b 4

Пример 4. Перемножить одночлены x 2 y 5 и (−6xy 2 )

Пример 5. Найти значение выражения

Деление одночленов

Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.

Например, разделим одночлен 8a 2 b 2 на одночлен 4ab. Запишем это деление в виде дроби:

Первый одночлен 8a 2 b 2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.

Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.

Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.

Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.

В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:

Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:

Пример 2. Разделить одночлен 12a 2 b 3 c 3 на одночлен 4a 2 bc

Пример 3. Разделить одночлен x 2 y 3 z на одночлен xy 2

Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.

и такое частное при перемножении с делителем x 2 будет давать в результате делимое 2x

Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное 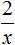целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.

Возведение одночлена в степень

Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.

Пример 1. Возвести одночлен xy во вторую степень.

Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена

Пример 2. Возвести одночлен −5a 3 b во вторую степень.

Пример 3. Возвести одночлен − a 2 bc 3 в пятую степень.

В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:

Пример 4. Представить одночлен 4x 2 в виде одночлена, возведённого в квадрат.

Пример 5. Представить одночлен 121a 6 в виде одночлена, возведённого в квадрат.

Таким образом, если произведение 11a 3 возвести во вторую степень, то получится 121a 6

(11a 3 ) 2 = 11 2 × (a 3 ) 2 = 121a 6

Разложение одночлена на множители

Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.

Пример 1. Разложить одночлен 3a 3 b 2 на множители

Данный одночлен можно разложить на множители 3, a, a, a, b, b

Либо степень b 2 можно не раскладывать на множители b и b

В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.

Пример 2. Разложить одночлен 10a 2 b 3 c 4 на множители.

Источник