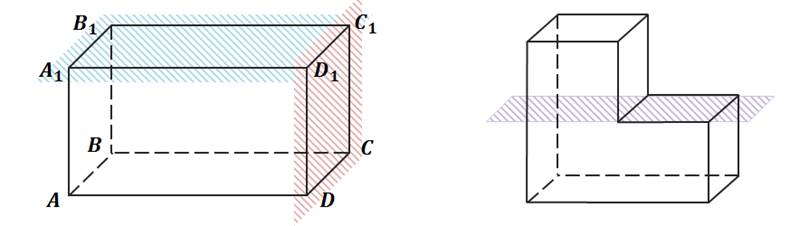
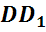Что называют гранями многогранника ребрами многогранника вершинами многогранника

§ 1. Пространственные фигуры

1. Какие геометрические фигуры называются плоскими; пространственными?

Плоскими называются фигуры, точки которых принадлежат одной плоскости. Пространственными называются фигуры, точки которых принадлежат нескольким плоскостям.

2. Какое тело называют многогранником?

Многогранником называют тело, ограниченное плоскими многоугольниками.

3. Что называют гранями многогранника; рёбрами многогранника; вершинами многогранника?

Гранями многогранника называют плоскости, ограниченные сторонами многоугольников, из которых состоит многогранник.

Вершинами многогранника называют вершины многоугольников, из которых состоит многогранник.

Рёбрами многогранника называют стороны многоугольников, из которых состоит многогранник.

4. Какой многогранник называется призмой?

Призмой называется многогранник, две грани которого — равные n-угольники, а остальные n граней — параллелограммы.

5. Что называют основаниями призмы; боковыми гранями призмы; боковыми рёбрами призмы?

Основаниями призмы называют равные грани-многоугольники этой призмы.

Боковыми гранями призмы называют параллелограммы, из которых состоит призма.

Боковыми рёбрами призмы называют рёбра боковых граней, не принадлежащие основаниям.

6. Какая призма называется прямой призмой; наклонной призмой?

Прямой называется призма, боковые грани которой являются прямоугольниками.

Наклонной называется призма, боковые рёбра которой не перпендикулярны рёбрам основания призмы.

7. Какая призма называется правильной призмой?

Правильной называется прямая призма, основания которой являются правильными многоугольниками.

8. Какая призма называется параллелепипедом; прямым параллелепипедом?

Параллелепипедом называется призма, основаниями которой являются параллелограммы.

Прямым параллелепипедом называется параллелепипед, боковые грани которого являются прямоугольниками.

9. Какой прямой параллелепипед называется прямоугольным параллелепипедом?

Прямоугольным параллелепипедом называется прямой параллелепипед, основания которого являются прямоугольниками.

10. Какие рёбра прямоугольного параллелепипеда называются его измерениями?

Измерениями прямоугольного параллелепипеда называются рёбра, которые сходятся в одной вершине.

11. Какой многогранник называется пирамидой?

Пирамидой называется многогранник, одна грань которого — многоугольник, а остальные — треугольники с общей вершиной.

12. Что называют основанием пирамиды; боковыми гранями пирамиды; вершиной пирамиды?

Основанием пирамиды называют её многоугольную грань.

Боковыми гранями пирамиды называют её треугольные грани.

Вершиной пирамиды называют общую вершину её боковых граней.

13. Какая пирамида называется правильной пирамидой?

Правильной называется пирамида, основание которой — правильный многоугольник, а отрезок, соединяющий её вершину с центром основания, перпендикулярен любой прямой, проведённой в плоскости основания через этот центр.

14. Какой отрезок называется апофемой правильной пирамиды?

Апофемой правильной пирамиды называют высоту боковой грани пирамиды, опущенную из вершины пирамиды.

15. Сформулируйте свойство боковых рёбер правильной пирамиды; боковых граней правильной пирамиды; апофем правильной пирамиды.

16. Чему равна площадь боковой поверхности правильной пирамиды?

Площадь боковой поверхности правильной пирамиды равна произведению полупериметра её основания и апофемы.

17. Какое тело называется цилиндром?

Цилиндром называется тело, которое получено вращением прямоугольника вокруг одной из его сторон.

18. Какое тело называется конусом?

Конусом называется тело, которое получено вращением прямоугольного треугольника вокруг одного из его катетов.

19. Какое тело называется шаром?

Шаром называется тело, которое получено вращением круга вокруг своего диаметра.

20. Верно ли, что:

а) количество вершин любой призмы — число чётное.

Верно. Если дана призма с n-угольником в основании, то количество вершин равно n + n = 2n. А 2n делится на 2.

б) количество рёбер любой призмы — число, кратное трём?

Верно. Если дана призма с n-угольником в основании, то количество ребер будет равно сумме n ребер нижнего основания, n ребер верхнего основания и n боковых ребер. Таким образом, количество ребёр равно n + n + n = 3n. А 3n делится на 3.

21. Найдите количество диагоналей семиугольной призмы.

Из одной вершины можно провести n – 3 диагоналей. Количество диагоналей будет равно n × (n – 3) = 7 × (7 – 3) = 28.

22. Существует ли пирамида, которая имеет 11 рёбер? Обоснуйте свой ответ.

Такой пирамиды не существует, поскольку пирамида всегда имеет чётное количество рёбер, т.к. количество рёбер n-угольной пирамиды равно 2n, а 2n делится на 2.

Источник

Что такое многогранник? Примеры

Примеры многогранников:

1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.

Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.

Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.

Популярное

Почему бумага? Иногда приходится слышать вопрос: «Почему вы выбрали для сборки многогранников такой материал как бумага (или точнее дизайнерский картон)? Это же.

Под руководством учителя математики Тимофеевой Татьяны Юрьевны ребята работали над проектом «Удивительный мир многогранников». Делали свои развертки и использовали развертки из.

Студией Артемия Лебедева (https://www.artlebedev.ru/) была предложена форма скворечника в виде многогранника. В качестве геометрической.

Нечасто удается встретить многогранники за пределами учебников математики. И если такие геометрические формы как куб, призма и цилиндр встречаются повседневно, то.

Когда мы готовили 36-ой выпуск «Волшебные грани», у наших коллег возник вопрос: «Почему мы опять собираемся говорить о правильных многогранниках.

Архитектурные шедевры находятся в разных уголках земного шара и отражают особенности человеческой души. Тайные людские желания воплощаются в форме необыкновенных зданий. В.

Существует концепция, что вершина многогранника отдает энергию, а плоскость энергию принимает. В том случае, если в многограннике вершин больше чем плоскостей, то он обладает.

Источник

Вершины, рёбра, грани многогранника

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

«Вершины, ребра, грани многогранника»

Многогранник (многогранная поверхность) – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело. Примером многогранника является куб, параллелепипед, призма и т.д.

Грани многогранника – это многоугольники, из которых составлен многогранник. Например, гранями параллелепипеда являются параллелограммы.

Стороны граней называются ребрами, а концы ребер – вершинами многогранника.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

Плоскость, по обе стороны от которой имеются точки многогранника, называется секущей плоскостью, а общая часть многогранника и секущей плоскости – сечением многогранника.

Многогранники бывают выпуклые и невыпуклые.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками.

Теорема Эйлера: в любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2.

Леонардо Эйлер (1707 – 1783) – швейцарец по происхождению, выдающийся математик. Большую часть жизни работал в России.

Решить задачу: Начертите произвольный прямоугольный параллелепипед, укажите все его вершины, ребра и грани. Проверьте выполнимость формулы Эйлера.

Выпуклые многогранники: а, б, д

Невыпуклые многогранники: в, г

8 вершин, 12 ребер, 6 граней

Формула Эйлера: 6 + 8 – 12 = 2

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 13. Многогранники

Перечень вопросов, рассматриваемых в теме:

Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.

Грани многогранника – многоугольники, ограничивающие многогранники.

Ребра многогранника – стороны граней многогранника.

Вершины многогранника – концы ребер многогранника (вершины граней многогранника).

Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.

Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.

Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.

Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)

Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)

Открытые электронные ресурсы:

Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.

Теоретический материал для самостоятельного изучения

К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.

Б)

Рисунок 1 – разные подходы к определению многоугольника

Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.

В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.

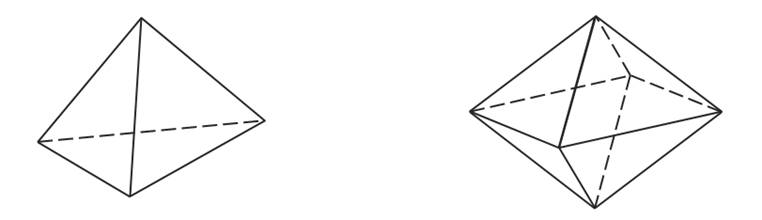
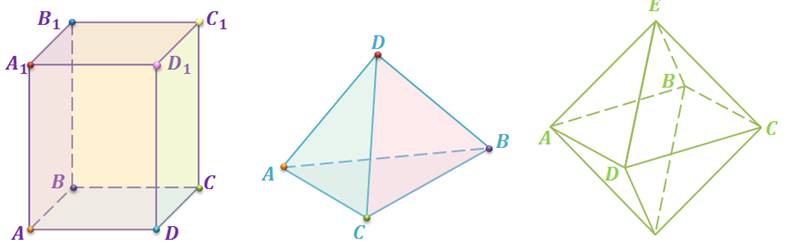
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)

Рисунок 2 – изображение октаэдра

Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».

Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).

Рисунок 3 – Виды многогранников

Сумма плоских углов при вершине выпуклого многогранника

Рисунок 4 – сумма плоских углов пи вершине многогранника

Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.

Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.

Примеры и разбор решения заданий тренировочного модуля

Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.

Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.

Задание 2. Сопоставьте геометрическим фигурам их вид

Б) пространственная фигура

Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.

Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б

Источник

Многогранник

Урок 44. Геометрия 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Многогранник»

На этом уроке мы поговорим о геометрическом теле, которое называют многогранником. А также узнаем, какими элементами обладают многогранники.

Как мы уже знаем, геометрия делится на два раздела – на планиметрию и стереометрию. Планиметрия изучает плоские геометрические фигуры и их свойства, т.е. фигуры, целиком расположенные в некоторой плоскости. Стереометрия изучает свойства фигур в пространстве. Пространственные геометрические фигуры, в отличие от плоских фигур, обладают вместимостью, т.е. они имеют объем. Такие фигуры называют еще объемными.

Все объемные фигуры можно распределить на две большие группы – круглые тела (это цилиндр, конус, сфера и шар), их называют телами вращения, и тела, которые содержат углы, вершины, грани и ребра (это призмы и пирамиды), такие тела называют многогранниками. Представления о геометрических телах дают нам окружающие нас предметы.

Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники простейшие фигуры на плоскости. С многогранными формами мы ежедневно встречаемся в жизни – это кубики, с которыми играют дети, многогранный карандаш, книги, многоэтажные дома, природные кристаллы, древние египетские пирамиды и т.д.

Ранее, в планиметрии при изучении многоугольников, мы говорили, что многоугольник – это замкнутая ломаная без самопересечений. Или иными словами, многоугольником называется часть плоскости, состоящая из простой замкнутой ломаной и ограниченной ею внутренней области.

При изучении многогранников мы же будем пользоваться вторым толкованием многоугольника.

Итак, уже само слово «многогранник» указывает на то, что это тело имеет много граней. Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.

Вы хорошо знакомы с одним из самых простых многогранников – прямоугольным параллелепипедом. Представление о прямоугольном параллелепипеде дают, например, спичечный коробок, холодильник, шкаф и другие тела.

Школьный кабинет также имеет форму прямоугольного параллелепипеда. Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников. Частным случаем прямоугольного параллелепипеда является куб. Напомню, что поверхность куба состоит из шести равных квадратов.

Можно сказать, что многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Это тело также называется многогранником.

На рисунке изображены два многогранника.

Первый из них называют – тетраэдром, второй – октаэдром. Они составлены соответственно из 4 и 8 треугольников. Что и отражено в их названиях: в переводе с греческого τετρα – «тетра» – четыре, а οκτώ – «окто» – восемь.

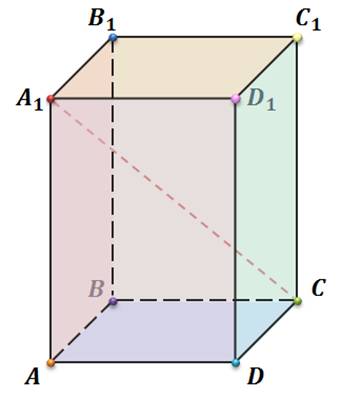
Обратим внимание, из чего состоит поверхность многогранника. Давайте рассмотрим, например, прямоугольный параллелепипед ABCDA₁B₁C₁D₁.

Как уже говорилось ранее, поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников. Т.е. его поверхность составлена из 6 многоугольников. Назовем их: , , , , , . Многоугольники, из которых составлен многогранник, называют его гранями. Заметим, что никакие две соседние грани многогранника не лежат в одной плоскости.

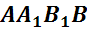
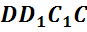
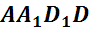
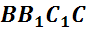
Стороны граней , , , , , , , , , , ,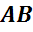

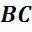
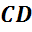
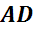
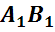
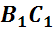
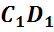
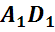
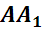
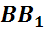
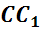
называются ребрами многогранника.

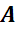
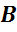
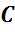
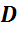
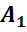
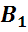
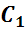
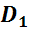
Концы рёбер , , , , , , , – вершины многогранника.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника, например, A₁C – называется диагональю многогранника. В данном случае, диагональ прямоугольного параллелепипеда.

Многогранники, также как и многоугольники бывают выпуклыми и невыпуклыми.

Смотрите, если провести плоскость, например, через грань DD₁C₁C, то весь многогранник будет лежать по одну сторону от этой плоскости. Аналогично, если провести плоскости и через остальные его грани, многогранник всегда будет расположен по одну сторону от этих плоскостей. Такой многогранник называется выпуклым.

Определение. Многогранник называется выпуклым, если он лежит по одну сторону от плоскости каждой своей грани.

Если это условие не выполняется, т.е. многогранник лежит по разные стороны хотя бы от одной плоскости, проходящей через грань, то многогранник называется невыпуклым.

На рисунке изображен пример невыпуклого многогранника. Если провести, например, плоскость через указанную грань, то видно, что одна часть многогранника расположена по одну сторону, а вторая его часть по другую сторону этой плоскости.

Задание. Сколько граней, рёбер и вершин имеет каждый из изображенных многогранников?

Итак, как мы уже говорили, поверхность прямоугольного параллелепипеда составлена из шести прямоугольников. Т.е. она состоит из 6 граней. Теперь посчитаем, сколько же у него ребер. Напомню, что стороны граней называются ребрами. Назовем их. Это АB, BC, CD, AD, A₁B₁, B₁C₁, C₁D₁, A₁D₁, AA₁, DD₁, BB₁ и CC₁. Итого, получили, что прямоугольный параллелепипед имеет 12 ребер. Концы этих ребер называются вершинами. Перечислим их. Это А, B, C, D, A₁, B₁, C₁, D₁. Т.е. у прямоугольного параллелепипеда – 8 вершин.

Следующее геометрическое тело тетраэдр. Его поверхность состоит из четырех треугольников. Т.е. имеет четыре грани. Его ребрами будут стороны АB, BC, АC, AD, BD, и CD. Т.е. тетраэдр имеет 6 ребер. Вершины тетраэдра А, B, C и D. Их 4.

И теперь рассмотрим октаэдр. Его поверхность состоит из 8 треугольников. Т.е. октаэдр имеет 8 граней. Также он имеет 12 ребер и 6 вершин.

Подведем итоги урока. На этом уроке мы узнали, какое геометрическое тело называют многогранником. Рассмотрели, какими элементами обладают многогранники. А именно, это грани, ребра и вершины. Узнали, что прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин. Познакомились с интересными многогранниками, которые называются тетраэдр и октаэдр. Узнали, что тетраэдр имеет 4 грани, 6 ребер и 4 вершины, а октаэдр – 8 граней, 12 ребер и 6 вершин.

Источник