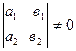Что называют геометрической моделью оригинала

Геометрические и графические компьютерные модели

Геометрическое моделирование — это процесс создания графических объектов.

Графический объект — это описание свойств материального объекта-оригинала (геометрической формы и окраски поверхности, размеров, размещения в пространстве).

Геометрическая модель — это модель графического объекта, отражающая геометрические свойства объекта-оригинала. Модель всегда является упрощением оригинала и обычно тем или иным его искажением. Модель можно представить как самостоятельное физическое изделие или составить из элементов сложной моделирующей установки (мозга или компьютера, т.е. можно формировать графический объект в мыслях, запоминать и записывать его ручными способами или с применением компьютера).

Задачами геометрического моделирования являются:

• создание моделей графических объектов;

• размещение моделей графических объектов в сцене (в ограниченной пространственной прямоугольной системе координат);

• организация движений графических объектов (анимация);

• представление изображений графических объектов на моно- и стереоэкранах (визуализация);

• формирование чертежной документации;

• создание слайдов и видеофильмов.

Геометрическое моделирование на компьютере исследуемых конструкций и процессов является сложным алгоритмическим процессом, включающим в себя:

• выбор или разработку математической модели описания геометрических объектов;

• размещение геометрических объектов в сцене с учетом ориентации;

• описание динамики объектов;

• перевод математической модели в машинную модель в фор-

матах, минимизирующих вычислительный процесс ее обработки;

• преобразование математической и машинной моделей;

• визуализацию машинной модели.

Для ввода и коррекции геометрической информации создаются графические редакторы, которые содержат библиотеки геометрических примитивов — точки, линии, плоскости, поверхности, простейшие геометрические тела (куб, параллелепипед, сферу, цилиндр, конус, тор и их модификации).

Из геометрических примитивов формируются детали, из деталей — объекты, а из объектов — сцены.

Графическиемодели:

· Графы (схема, отображающая элементный состав системы и структуру связей, называется графом. Составными частями графа являются вершины и ребра)

Геоинформационные модели.

Геоинформационное моделирование базируется на создании многослойных элекронных карт, в которых опорный слой описывает географию определенной территории, а каждый из остальных — один из аспектов состояния этой территории. На географическую карту могут быть выведены различные слои объектов: города, дороги, аэропорты и др.

Широкое распространение получили интерактивные географические карты (мира, различных частей света, России, Москвы и других городов) в Интернете. Такие карты обычно реализуются с использованием векторной графики и поэтому дают возможность пользователю выбирать нужный ему масштаб. Карты связаны с базами данных, которые хранят всю необходимую информацию об объектах, изображенных на картах.

Например, на картографическом сервере можно сначала выбрать нужную карту из раскрывающегося списка, а затем выбрать вариант отображения карты (политико-административное деление, население, транспорт и так далее) — Если выбрать какой-либо регион на карте и щелкнуть на нем мышью, то появится окно с дополнительной информацией.

Геоинформационные модели позволяют с помощью географических карт представлять статистическую информацию о различных регионах. Хранящаяся в базах данных информация о количестве населения, развитии промышленности, загрязнении огружающей среды и др. может быть связана с географическими картами и отображена на них. Отображение информации может производиться различными способами: закрашиванием регионов различными цветами, построением диаграмм и так далее.

Можно построить в электронных таблицах Excel с использованием специальной надстройки Microsoft Data Map геоинформационную модель, отображающую информацию о количестве населения в различных странах мира.

Табличные модели.

Представление информации в табличной форме широко распространено. Уже в школьной жизни приходится встречаться с массой таблиц: расписание занятий, журнал успеваемости, график дежурств, таблица Менделеева, таблицы физических свойств веществ, таблицы исторических дат и многое другое. Информация в таблицах обязательно упорядочена по какому-то принципу. Например, в классном журнале — в алфавитном порядке фамилий учеников; в расписании занятий — по дням недели и номерам уроков и т.д. Такая упорядоченность позволяет быстро находить в таблице нужные сведения.

Чаще всего используются прямоугольные таблицы, состоящие из строк и столбцов (граф). В верхней строке таблицы обычно располагаются заголовки граф.

· объект-свойство (каждая строка такой таблицы относится к конкретному объекту)

· объект-объект (отражают взаимосвязь между различными объектам)

Информационные модели.

Информационная модель — модельобъекта, представленная в виде информации, описывающей существенные для данного рассмотрения параметры и переменные величины объекта, связи между ними, входы и выходы объекта и позволяющая путём подачи на модель информации об изменениях входных величин моделировать возможные состояния объекта. Информационныемодели нельзя потрогать или увидеть, они не имеют материального воплощения, потому что строятся только на информации. Информационная модель — совокупность информации, характеризующая существенные свойства и состояния объекта, процесса, явления, а также взаимосвязь с внешним миром.

Информационные модели делятся на описательные и формальные.

Источник

Геометрическое моделирование

Модель — это упрощенное представление реального устройства и/или протекающих в нем процессов, явлений.

Построение и исследование моделей, то есть моделирование, облегчает изучение имеющихся в реальном устройстве (процессе, …) свойств и закономерностей. Применяют для нужд познания (созерцания, анализа и синтеза).

Моделирование является обязательной частью исследований и разработок, неотъемлемой частью нашей жизни, поскольку сложность любого материального объекта и окружающего его мира бесконечна вследствие неисчерпаемости материи и форм её взаимодействия внутри себя и с внешней средой.

Моделирование — исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя.

В силу многозначности понятия «модель» в науке и технике не существует единой классификации видов моделирования: классификацию можно проводить по характеру моделей, по характеру моделируемых объектов, по сферам приложения моделирования (в технике, физических науках, кибернетике и т. д.). Например, можно выделить следующие виды моделирования:

· Графическое и геометрическое моделирование

Математическое моделирование — это процесс построения и изучения математических моделей.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.

Во многих приложениях машинной графики возникает потребность в представлении трехмерных тел (вычислительный эксперимент, автоматизация проектирования, роботизация, вычислительная томография, тренажеры, видеографика и т.д.).

При решении первой задачи в общем случае может потребоваться задание бесконечного количества координат точек. Чаще же всего объект с той или иной точностью аппроксимируют некоторым конечным набором элементов, например, поверхностей, тел и т.п.

o каркасное представление, когда тело описывается набором ребер,

o поверхностное, когда тело описывается набором ограничивающих его поверхностей,

Важно отметить, что 3D системы существенно ориентируются на область приложений так как многие характерные для них задачи, выполняемые программным путем, стоят очень дорого и сильно зависят от выбора возможных моделей. Типичными такими задачами, в частности, являются получение сечений и удаление невидимых частей изображения. Обычно имеется много вариантов реализации различных моделей в большей или меньшей степени эффективных в зависимости от различных областей приложений и решаемых задач. Поэтому в 3D системах стремятся использовать многообразие моделей и поддерживать средства перехода от одной модели к другой.

Другим важным обстоятельством является то, что для современных систем характерно стремление моделировать логику работы, принятую пользователем. Это требует наличия средств перехода от модели, удобной для пользователя, к модели удобной для визуализации (модели тел в виде граней).

Элементы моделей

При формировании 3D модели используются:

o двумерные элементы (точки, прямые, отрезки прямых, окружности и их дуги, различные плоские кривые и контуры),

o поверхности (плоскости, поверхности, представленные семейством образующих, поверхности вращения, криволинейные поверхности),

o объемные элементы (параллелепипеды, призмы, пирамиды, конусы, произвольные многогранники и т.п.).

Из этих элементов с помощью различных операций формируется внутреннее представление модели.

Процесс моделирования

Процесс моделирования включает три элемента:

модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.

Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.

На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.

На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.

Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.

Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.

Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.

Методы построения моделей

Построение с использованием отношений

Построение с использованием отношений заключается в том, что задаются:

· элемент подлежащий построению и список отношений и элементы, к которым относятся отношения.

Например, построение прямой, проходящей через точку пересечения двух других прямых и касательную к окружности.

При общем способе реализации построение по заданным отношениям можно представить в виде двухшаговой процедуры:

· на основе заданных типов отношений, элементов и параметров строится система алгебраических уравнений,

· решается построенная система уравнений.

Основные проблемы такого способа заключаются в следующем:

· построенная система уравнений может иметь несколько решений, поэтому требуется выбрать одно из них, например, в диалоговом режиме,

· система уравнений может оказаться нелинейной, решаемой приближенными методами, что может потребовать диалога для выбора метода(ов) приближенного решения.

В связи с отмеченными проблемами общий подход реализован только в наиболее современных системах и при достаточно высоком уровне разработчиков в области вычислительной математики [8].

Большинство же систем реализует частный подход, первым приходящий в голову и заключающийся в том, что для каждой триады, включающей строящийся элемент, тип отношения и иные элементы, затрагиваемые отношением, пишется отдельная подпрограмма (например построение прямой, касательной к окружности в заданной точке). Требуемое построение осуществляется выбором из меню и тем или иным вводом требуемых данных [6,].

Понятно, что перспективы за общим подходом с разумным использованием частных решений. Вместе с тем устаревшие системы типа AutoCad скорее всего также будут продолжать использоваться в силу распространенности, сложившегося круга обученных пользователей и т.п.

Сплайны

Сплайн — функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.

Сплайны имеют многочисленные применения как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.

Виды сплайнов

Как отмечалось выше, существует большое количество конструкций, которые называют сплайнами. Поэтому необходимо внести определенную классификацию в это многообразие, имея целью выделить те признаки, которые позволят выбрать сплайны годные для конкретной прикладной задачи.

Вид фрагментов сплайна. То, что сплайн состоит из фрагментов одинакового вида, является одним из ключевых признаков, что отличает его от других кусковых функций.

Самые известные сплайны — состоящие из фрагментов — алгебраических полиномов не выше заданной степени. Как правило, это кубические полиномы, или полиномы нечётных степеней: первой, третьей (кубический), пятой степени. Более высокие степени применяют редко из-за усложнения расчетов и сложностей, описанных в предыдущем разделе. Основным их преимуществом является простота расчетов и анализа. Недостатком является то, что относительно мало реальных физических процессов соответствуют этой зависимости.

Экспоненциальные сплайны. Если гибкую металлическую линейку, зафиксированную в узлах, натянуть, то решением дифференциального уравнения будет не алгебраический полином, а экспонента. Поэтому такие сплайны называют также напряженными. Экспонента описывает многие физические процессы в динамических системах. Недостатком является трудоёмкость расчета.

Тригонометрическими являются сплайны, фрагменты которых описываются тригонометрическими полиномами. Имеют достаточно сложные расчетные выражения. Более пятидесяти различных по виду фрагментов сплайнов описаны в работах Б. А. Попова.

Также существуют рациональные сплайны и сплайны Паде. Их особенностью является возможность разрыва производных на фрагментах, при непрерывности в узлах. М. Ансерме строит фракциональные сплайны, где фрагменты заданы с помощью гамма-функции.

Целесообразность применения фрагментов определенного вида основана на конкретных условиях задачи и ограничениях реализации. Как правило, основное требование — это достижение заданной точности интерполяции при приемлемых затратах времени и ресурсов на реализацию. Удачный выбор фрагментов, который соответствует характеру процесса, позволяет сократить время вычислений и требуемый объём памяти.

Число фрагментов. Очевидно, что минимальное число фрагментов — один. Классическое определение сплайна ограничивает число фрагментов определенным числом на конечном отрезке. Однако можно строить сплайны и с бесконечным числом фрагментов, а реально эти методы и алгоритмы, которые не нуждаются в информации об определенном количестве фрагментов. Представителями этих сплайнов являются кардинальные сплайны, исследованные Шенбергом. Для построения сплайнов с неограниченным числом фрагментов лучше подходят локальные сплайны.

Ширина фрагментов. Следует выделить сплайны с равной шириной фрагментов. Это позволяет значительно упростить расчетные выражения, ускорить работу алгоритмов и снизить затраты на реализацию. Определенного упрощения можно достичь за счёт применения фрагментов с кратной шириной. Существуют сплайны с нулевой шириной фрагментов (Де Бур). Это приводит к кратности узлов и возможности приближать сплайны с неразрывными фрагментами разрывных функций. Расчетные выражения получают в результате предельных переходов. Сплайны могут иметь также фрагменты с бесконечной шириной. Эти фрагменты должны быть крайними. Иногда это позволяет естественно задать краевые условия.

Условия стыковки фрагментов. Еще один важный признак, что отличает сплайны. Когда идет речь о сплайнах, как правило, считают, что фрагменты стыкуются гладко. То есть обеспечивается непрерывность значений и первой производной. Понятие дефекта сплайна связано с числом непрерывных производных, которые имеет функция-фрагмент определенного вида и числом производных, непрерывность которых гарантирована в узлах. Экспонента, синусоида имеют бесконечное число производных. Для них это понятие не имеет смысла. Поэтому удобнее говорить прямо о числе производных, непрерывность которых гарантирована в узлах сплайна. Практически речь идет о непрерывности значений и первой, максимум второй производной. Разрыв второй и высших производных визуально не заметно, поэтому учитывается редко. Понятно, что первая производная в точках стыка может задаваться по-разному. Наиболее распространены два приёма. Значение первой производной выбирается так, чтобы обеспечить непрерывность второй (глобальные кубические сплайны минимального дефекта). Первая производная равняется первой производной интерполируемой функции (возможно приближенно) в эрмитовых сплайнах.

Краевые условия. Если сплайны имеют ограниченное число фрагментов, то, естественно, у них отсутствуют крайние фрагменты слева и справа, поэтому крайние узлы не с чем стыковать. Исключением являются лишь периодические сплайны, которые имеют естественное продолжение. Иногда естественными называют краевые условия с нулевой производной, хотя никаких оснований считать их более естественными, чем другие, нет. Если сплайн имеет фрагменты одинаковой ширины, считают недостающие фрагменты той же ширины. Другой вариант — это считать недостающие фрагменты продлёнными в бесконечность. Преимущество такого подхода в возможности экстраполяции. Можно считать ширину фрагментов нулевой. Расчетные выражения получают предельными переходами. Если взглянуть на краевые условия с точки зрения формирования сплайна из базисных функций, то они сводятся к продолжению соответствующих локальных базисных функций. Ширина соседних фрагментов влияет на их форму. А простое обрезание часто приводит к осцилляции и росту погрешности на краях. Важное значение краевые условия имеют при обработке изображений и в задачах с экстраполяцией.

Дополнительные ограничения. Они чаще всего касаются производных в узлах. Иногда они вытекают из физики процесса. Условия: неотъемлемость значений, равенство моментов, площадей, условия нормирования. Дополнительные условия иногда упрощают анализ свойств сплайнов, но могут серьезно затруднять построение и затраты реализации.

Сетка точек интерполяции. Может существенно влиять на эффективность расчетов. Важны случаи равномерной сетки и равномерной сетки, с расстоянием между точками, кратным расстоянию между узлами сплайна.

Локальные свойства базисных функций. Сплайн можно представить как сумму взвешенных базисных сплайнов. Существенным является ширина этих базисных функций. Так, в глобальных сплайнах базисные сплайны ненулевые на всём отрезке интерполяции. Хотя стоит заметить, что с определенной точностью (достаточной для многих технических расчетов) их можно считать локальными. У локальных сплайнов ширина базисных функций невелика (четыре фрагмента у кубических эрмитовых сплайнов). Это существенно влияет на эффективность расчетов и затраты реализации.

Форма представления. Функции, задающие фрагменты сплайна, как правило, зависят от множества параметров, благодаря которым они меняют свою форму. Значения параметров на каждом из фрагментов индивидуальны. Эти параметры могут задавать конкретный сплайн. Для полиномиальных сплайнов это полиномиальные коэффициенты. Так, сплайн можно представить множеством параметров функций на каждом из фрагментов. Назовем это представление пофрагментным. Такое представление является наглядным, часто имеет явный физический смысл. Но число параметров является чрезмерным. Так, для кубического сплайна необходимо иметь 4 * (r-1) параметров (r — число узлов сплайна). Значительно более компактным является представление сплайна в виде полинома, через базисные сплайн-функции в виде:

где — базисные сплайн-функции (как правило локальные), — числовые коэффициенты, задающие вес базисных функций при формировании сплайна. Число параметров, задающих сплайн, равно числу узлов сплайна. Между параметрами функции на фрагменте и коэффициентами полинома-сплайна существует зависимость, что позволяет с одними коэффициентами находить другие, хотя формулы могут иметь достаточно сложный вид.

Содержание коэффициентов сплайна. Как отмечалось в предыдущем пункте, содержание параметров сплайна при пофрагментном представлении определяется типом функции. При полиномиальном представлении следует выделить случай, когда коэффициенты имеют тот же физический смысл, что и входные данные. То есть, коэффициенты являются значениями сплайна в узлах. Такую форму называют Лагранжевой, по аналогии с полиномом Лагранжа. Следует заметить, что базисные сплайны этой формы равны единице в центральном узле и нулю во всех остальных.

Особые сплайны. В ряде случаев рассматривают функции, которые находятся близко к границе между сплайнами и обычными функциями, а также сплайнами и кусковыми функциями. К примеру, это сплайны, состоящие из двух фрагментов. Имеют упрощенный вариант построения, но особое внимание следует уделять краевым условиям.

Аффинные преобразования

Аффинные преобразования плоскости

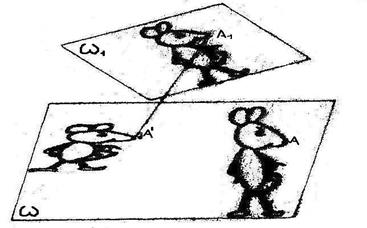
Аффинным преобразованием α называется такое преобразование плоскости, которое всякую прямую переводит в прямую и сохраняет отношение, в котором точка делит отрезок.

На рис.1: L’= α(L), A’=α(A), B’=α(B), C’=α(C), |

Приведем пример аффинного преобразования, не сводящегося к ранее рассмотренным. С этой целью сначала рассмотрим параллельное проектирование плоскости на плоскость.

Отметим следующие свойства параллельного проектирования.

1) Образом всякой прямой а1 является прямая.

В самом деле, прямые, проектирующие точки прямой а1, образуют плоскость (она проходит через а1 параллельно l), которая при пересечении с w дает образ прямой а1 – прямую а(рис.2).

2) Отношение, в котором точка делит отрезок, сохраняется, т.е.

(рис.2)

Сразу следует из теоремы о пересечении сторон угла параллельными прямыми.

Перейдем непосредственно к построению примера аффинного преобразования.

Возьмем два экземпляра плоскости w и один из них переместим в другое положение w1(рис.3). Новое положение какой-либо точки Аєw обозначим А1єw1. Теперь плоскость w1 спроектируем в каком-нибудь положении на w, проекцию точки А1 обозначим А’.

Получилось преобразование плоскости w на себя, при котором . В силу симметричных свойств параллельного проектирования для данного преобразования выполняются оба требования определенного аффинного преобразования, следовательно, построенное сейчас преобразование –перспективно- аффинное.

3)Основная теорема. Каковы бы ни были 2 аффинных репера и , существует единственное аффинное преобразование, которое первый переводит во второй.

Образом прямой l, имеющей в репере R уравнение ах+ву+с=0, будет линия l’, которая в R’ имеет то же самое уравнение. Значит, l’- прямая(рис.5). Следовательно, образом произвольной прямой является прямая.

рис. 5

Пусть теперь точка С(х,у) делит отрезок, соединяющий точки А(х1,у1), В(х2,у2) в отношении

А так как образы этих точек- А’,В’,С’ имеют те же координаты(в другой системе), то и, следовательно,

Итак для преобразования α выполнены оба требования определения, значит α- аффинное преобразование.

Единственность доказательства от противного. Пусть существует два аффинных преобразования α1 и α2, при которых . Тогда найдется такая точка А, что , где (рис.6). Обозначим через К точку пересечения прямых ОА и Е1Е2(если эти прямые параллельны, то надо взять Е1А, ОЕ2, если и эти прямые параллельны, надо взять Е2А и ОЕ1). Так как , то образом точки К будет точка К’1-точка пересечения прямых . В силу определения аффинного преобразования:

Аналогично для преобразования α2.

Таким образом

Первое из этих равенств показывает, что точки К’1 и К’2 совпадают, а тогда из второго следует А’1=А’2, что противоречит А. Полученное противоречие доказывает теорему.

Основную теорему можно сформулировать иначе: каковы бы ни были два треугольника, существует единственное аффинное преобразование, переводящее один в другой.

Доказанная основная теорема делает понятие аффинного преобразования конструктивным. Аффинное преобразование задается парой произвольных аффинных реперов.

4)Уравнения аффинного преобразования получаются из основной теоремы и формул преобразования аффинных координат точно так же, как и уравнения движения и подобия. Пусть даны два репера и (рис. 7).

O'(c1,c2),

Эти уравнения записаны в аффинной системе координат. В частности они действуют и в прямоугольных декартовых координатах.

2.2 Свойства аффинного преобразования

1. Образом параллельных прямых являются параллельные прямые.

Доказательство от противного. Предположим, что образом параллельных прямых l и m являются пересекающиеся в точке А’ прямые l’ и m'(рис.8). В силу взаимной однозначности преобразования точка имеет прообраз, который обозначим А. Но так как А’єl’, то Аєl. Аналогично Аєm. Это противоречит параллельности прямых l и m.

2.При аффинном преобразовании сохраняется отношение двух отрезков, расположенных на одной прямой: (рис.9)

В самом деле, по определению аффинного преобразования:

.

3.При аффинном преобразовании сохраняется отношение параллельных отрезков.

Дано: АВ||СD. По свойству 2 будет также А’В’||С’D'(рис.10)

Надо доказать:

Для доказательства проведем АС, затем DL||AC. Построим также А’С’ и D’L’||A’C’. По свойству 2 прямая DL переходит в D’L’ и значит, . Теперь по определению: . Но AL=CD, A’L’=C’L’, поэтому отсюда сразу получается требуемое.

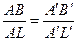
4.При аффинном преобразовании угол и отношение произвольных отрезков, вообще говоря, не сохраняются, так как любой треугольник можно перевести в любой другой. Поэтому высота и биссектриса треугольника преобразуются обычно в другие линии, медиана же переходит в медиану, так как середина отрезка переходит в середину.

5. При аффинном преобразовании параллелограмм переходит в параллелограмм, трапеция в трапецию.

Источник