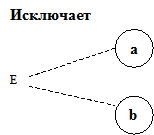Что называют функциональной диаграммой

Функциональные диаграммы

Функциональными называют диаграммы, в первую очередь отражающие взаимосвязи функций разрабатываемого программного обеспечения.

Они создаются на ранних этапах проектирования систем, для того чтобы помочь проектировщику выявить основные функции и составные части проектируемой системы и, по возможности, обнаружить и устранить существенные ошибки. Современные методы структурного анализа и проектирования предоставляют разработчику определённые синтаксические и графические средства проектирования функциональных диаграмм информационных систем.

4.1. Методология SADT

Функциональная модель SADT отображает функциональную структуру объекта, т.е. производимые им действия и связи между этими действиями. Основные элементы этой методологии основываются на следующих концепциях:

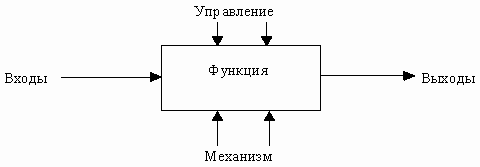
· графическое представление блочного моделирования. На SADT-диаграмме функции представляется в виде блока, а интерфейсы входа/выхода в виде дуг, соответственно входящих в блок и выходящих из него. Интерфейсные дуги отображают взаимодействие функций друг с другом;

· строгость и точность отображения.

Правила SADT включают:

· уникальность меток и наименований;

· ограничение количества блоков на каждом уровне декомпозиции;

· синтаксические правила для графики;

· отделение организации от функции;

· разделение входов и управлений.

Диаграммы – главные компоненты модели, все функции программной системы и интерфейсы на них представлены как блоки и дуги. Место соединения дуги с блоком определяет тип интерфейса. Дуга, обозначающая управление, входит в блок сверху, в то время как информация, которая подвергается обработке, представляется дугой с левой стороны блока, а результаты обработки – это дуги с правой стороны. Механизм (человек или автоматизированная система), который осуществляет операцию, представляется в виде дуги, входящей в блок снизу (рис. 8).

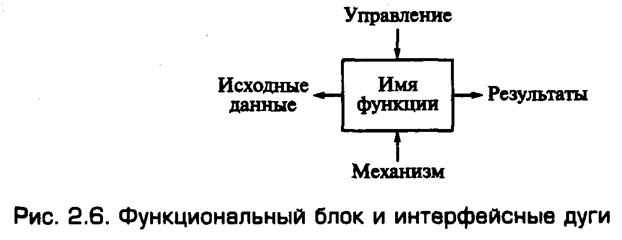
Рис. 8. Функциональный блок и интерфейсные дуги

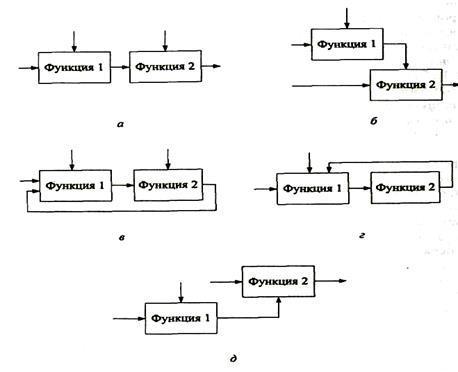
Блоки на диаграмме размещают по «ступенчатой» схеме в соответствии с последовательностью их работы или доминированием, которое понимается как влияние, оказываемое одним блоком на другие. В функциональных диаграммах SADT различают пять типов влияний блоков друг на друга:

· вход-выход блока подается на вход блока с меньшим доминированием, т.е. следующего (рис. 9, а);

· управление – выход блока используется как управление для блока с меньшим доминированием (рис. 9, б);

· обратная связь по входу – выход блока подается на вход блока с большим доминированием (рис. 9, в);

· обратная связь по управлению – выход блока используется как управляющая информация для блока с большим доминированием (рис. 9, г);

· выход-исполнитель – выход блока используется как механизм для другого блока (рис. 9, д).

4.2. Иерархия диаграмм

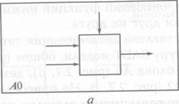
Прежде всего, вся система представляется в виде простейшей компоненты – одного блока и дуг, представляющих собой интерфейсы с внешними по отношению к данной системе функциями. Имя блока является общим для всей системы.

Затем блок, который представляет систему в целом, детализируется на следующей диаграмме. Он представляется в виде нескольких блоков, соединенных интерфейсными дугами (рис. 10). Каждый блок детальной диаграммы представляет собой подфункцию, границы которой определены интерфейсными дугами. Каждый из блоков детальной диаграммы может быть также детализирован на следующей в иерархии диаграмме. На каждом шаге декомпозиции более общая диаграмма называется родительской для более детальной диаграммы.

Все диаграммы связывают друг с другом иерархической нумерацией блоков: первый уровень – АО, второй – А1, А2 и т. п., третий – А11, А12, А13 и т. п., где первые цифры – номер родительского блока, а последняя – номер конкретного блока детальной диаграммы.

Рис. 10. Структура SADT-модели. Декомпозиция диаграмм

Дуги, входящие в блок и выходящие из него на диаграмме верхнего уровня, являются точно теми же самыми, что и дуги, входящие в диаграмму нижнего уровня и выходящие из нее, потому что блок и диаграмма представляют одну и ту же часть системы.

Пример 1.Разработку функциональных диаграмм продемонстрируем на примере уточнения спецификаций программы сортировки одномерного массива с использованием нескольких методов.

Диаграмма, представленная на рис. 11, а, является диаграммой верхнего уровня. Она иллюстрирует исходные данные программы и ожидаемые результаты.

Диаграмма, представленная на рис. 11, б, детализирует функции программы. На ней показаны три блока: Меню, Сортировка, Вывод результата. Для каждого блока определены исходные данные, управляющие воздействия и результаты. На детализирующей диаграмме используются следующие обозначения:

I1 – размер массива;

R1 – вывод описания метода;

R2 – отсортированный массив.

Рис. 11. Функциональные диаграммы для системы исследования функций:

Источник

ФУНКЦИОНАЛЬНЫЕ ДИАГРАММЫ

Характеристика функциональных диаграмм (SADT) — диаг­раммы SADT отражают взаимные связи функций разрабатываемого программного обеспечения. Они создаются на ранних стади­ях проектирования систем, для того чтобы помочь проектировщи­ку выявить основные функции и составные части проектируемой программной системы и, по возможности, обнаружить и устра­нить существенные ошибки. Для создания функциональных диаг­рамм предлагается использовать методологию SADT, предложен­ную Д.Россом. На основе методологии SADT была построена из­вестная методология описания сложных систем IDEFO (Icam DEFinition), являющаяся основной частью программы ICAM (ин­тегрированная компьютеризация производства), проводимой по инициативе ВВС США. Применение методологии SADT позволя­ет построить модель, состоящую из диаграмм, фрагментов тек­стов и глоссария, имеющих ссылки друг на друга. Диаграммы — главные компоненты модели. Функции системы и интерфейсы представлены на диаграммах в виде блоков и дуг. Место соедине­ния дуги с блоком определяет тип интерфейса. Управляющая ин­формация входит в блок сверху, в то время как информация, ко­торая подвергается обработке, показана с левой стороны блока, а результаты выхода даны с правой стороны. Механизм (человек или автоматизированная система), осуществляющий операцию, представлен дугой, входящей в блок снизу (рис. 2.6).

Одна из наиболее важных особенностей методологии SADT — постепенное введение все больших уровней детализации по мере создания диаграмм, отображающих модель. Построение SADT-модели начинается с представления всей системы в виде простей­шей компоненты — одного блока и дуг, изображающих интер­фейсы с функциями вне системы. Поскольку единственный блок представляет всю систему как единое целое, имя, указанное в блоке, является общим. Это верно и для интерфейсных дуг — они также представляют собой полный набор внешних интерфейсов системы в целом.

Затем блок, в котором система дана в качестве единого моду­ля, детализируется на другой диаграмме с помощью нескольких

блоков, соединенных интерфейсными дугами. Эти блоки пред­ставляют основные подфункции исходной функции. Данная де­композиция выявляет полный набор подфункций, каждая из ко­торых представлена как блок, границы которого определены ин­терфейсными дугами. Каждая из этих подфункций может быть декомпозирована подобным образом для более детального пред­ставления. Во всех случаях каждая подфункция может содержать только те элементы, которые входят в исходную функцию. Кро­ме того, модель не может опустить какие-либо элементы, т.е., как уже отмечалось, родительский блок и его интерфейсы обеспечи­вают контекст. К нему нельзя ничего добавить, и из него не мо­жет быть ничего удалено.

Модель SADT представляет собой серию диаграмм с сопрово­дительной документацией, разбивающих сложный объект на со­ставные части, представленные в виде блоков. Детали каждого из основных блоков показаны в виде блоков на других диаграммах. Каждая детальная диаграмма является декомпозицией блока из более общей диаграммы. На каждом шаге декомпозиции более общая диаграмма называется родительской для более детальной диаграммы.

Дуги, входящие в блок и выходящие из него на диаграмме верхнего уровня, являются точно теми же самыми, что и дуги, входящие в диаграмму нижнего уровня и выходящие из нее, по­тому что блок и диаграмма представляют одну и ту же часть сис­темы.

Стрелки, приходящие с родительской диаграммы или уходя­щие на нее, нумеруют, используя символы и числа. Символ обо­значает тип связи: / — входные, С — управляющие, М — меха­низмы, R — результаты. Число — номер связи по соответствую­щей стороне родительского блока, считая сверху вниз и слева направо. Все диаграммы связывают друг с другом иерархической нумерацией блоков: начальный уровень — АО, следующий — А1, А2 и т.п., следующий — All, А12, А13 и т.д., где первая цифра — номер родительского блока, а последняя — номер конкретного субблока родительского блока. Детализацию завершают при полу­чении функций, назначение которых хорошо понятно как заказ­чику, так и разработчику. Эти функции описывают, используя ес­тественный язык или псевдокоды. В процессе построения иерар­хии диаграмм фиксируют всю уточняющую информацию и стро­ят словарь данных, в котором определяют структуры и элементы данных, показанных на диаграммах. Таким образом, в результате получают спецификацию, которая состоит из иерархии функци-

Рис. 2.7. Структура SADT-модели. Декомпозиция диаграмм

ональных диаграмм, описаний функций нижнего уровня и слова­ря, имеющих ссылки друг на друга.

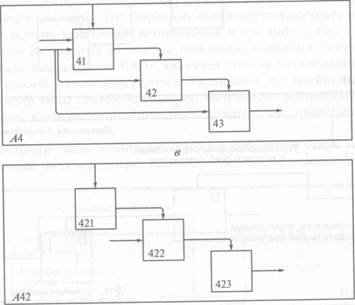
На рис. 2.7 представлена декомпозиция четырех диаграмм, по­казывающая структуру SADT-модели, общее (рис. 2.7, а) и деталь­ное представление блока АО (рис. 2.7, б), декомпозицию блоков А4 (рис. 2.7, в) и А42 (рис. 2.7, г). Не присоединяемые дуги соот­ветствуют входам, управлениям и выходам родительского блока. Источник или получатель этих дуг может быть обнаружен только на родительской диаграмме. Не присоединяемые концы должны соответствовать дугам на исходной диаграмме. Все граничные дуги должны продолжаться на родительской диаграмме, чтобы она была полной и непротиворечивой.

Управляющая дуга, переносимая с родительской диаграммы

Входная дуга, переносимая с родительской диаграммы

Дуга, продолжающаяся на родительской диаграмме

Рис. 2.8. Соответствие интерфейсных дуг родительской (а) и детальной (б) диаграмм

Функции блоков 2 и 3 могут выполняться параллельно

Рис. 2.9. Пример одновременного выполнения функций

Каждый компонент модели может быть декомпозирован на другой диаграмме, т.е. каждая диаграмма иллюстрирует «внутрен­нее строение» блока на родительской диаграмме.

На рис. 2.8, а, б и рис. 2.9 представлены различные варианты выполнения функций и соединения дуг с блоками.

На SADT-диаграммах не указаны явно ни последовательность, ни время. Обратные связи, итерации, продолжающиеся процессы и перекрывающиеся (по времени) функции могут быть изображе­ны также с помощью дуг. Обратные связи могут выступать в виде комментариев, замечаний, исправлений и т.д. (рис. 2.10).

Одним из важных моментов при моделировании системы с помощью методологии SADT является точная согласованность типов связей между функциями. Различают, по крайней мере, следующие типы связей: случайная; логическая; временная; про­цедурная; коммуникационная; последовательная; функциональ­ная.

Случайная связь возникает, когда конкретная связь между функциями мала или полностью отсутствует. Это относится к си-

Рис. 2.10. Пример обратной связи

туации, когда имена данных на SADT-дугах в одной диаграмме имеют малую связь друг с другом.

Логическая связь — данные и функции собираются вместе, поскольку попадают в общий класс или набор элементов, но не­обходимых функциональных отношений между ними при этом не обнаруживается.

Согласовывать А и В

Рис. 2.11. Типы связей:

Временная связь представляет функции, связанные во време­ни, когда данные используются одновременно или функции вклю­чаются параллельно, а не последовательно.

При процедурной связи функции сгруппированы вместе, по­скольку они выполняются в течение одной и той же части цикла или процесса (рис. 2.11, а).

Диаграммы демонстрируют коммуникационную связь, когда блоки группируются вследствие того, что они используют одни и те же входные данные и (или) производят одни и те же выходные данные (рис. 2.11, б).

При последовательной связи выходные данные одной функции служат входными данными для другой функции. Связь между эле­ментами на диаграмме является более тесной, чем на рассмотрен­ных выше уровнях, поскольку моделируются причинно-следствен­ные зависимости (рис. 2.11, в).

Диаграмма отражает полную функциональную связь при нали­чии полной зависимости одной функции от другой. Диаграмма, которая является чисто функциональной, не содержит чужерод­ных элементов, относящихся к последовательному или более слабому типу связности. Одним из способов определения фун­кционально связанных диаграмм является рассмотрение двух блоков, связанных через управляющие дуги, как показано на рис. 2.11, г.

В математических терминах необходимое условие для простейшего типа функциональной связности (рис. 2.11, г) имеет следующий вид: С = д(В) = g(f(A)).

Метод SADT может использоваться для моделирования самых разнообразных систем и для определения требований и функций. В существующих системах метод SADT может применяться для анализа функций, выполняемых системой, и указания механиз­мов, посредством которых они осуществляются.

Пример разработки функциональной диаграммы программы построения графиков. Разработку функциональных диаграмм продемонстрируем на примере уточнения спецификаций про­граммы построения графиков и таблиц функций одной перемен­ной.

На рис. 2.12, а показана диаграмма верхнего уровня, на кото­рой хорошо видно, что является исходными данными для про­граммы и получения каких результатов мы ожидаем.

Диаграмма на рис. 2.12, б уточняет функции программы. На ней показаны четыре блока: ввод—выбор и ее разбор, добавле­ние функции в список, построение таблицы значений и построе-

Построение графиков/таблиц функций

Ввод/выбор функции и ее разбор

Добавление функции в список

Построение таблицы значений

Построение графика значений

Рис. 2.12. Функциональные диаграммы для системы исследования функций:

а — диаграмма верхнего уровня; б — уточняющая диаграмма

ние графика функции. Для каждого блока определены исходные данные, управляющие воздействия и результаты. Согласно прави­лам обозначения входов—выходов, имеющих продолжение на ро­дительской диаграмме, на данной диаграмме использованы следую­щие обозначения: Л — функция; 12 — отрезок; /3 — шаг; С1 — вид график—таблица; RI — график функции на отрезке; R2 — таблица значений функции на отрезке.

Словарь в этом случае должен содержать описание всех дан­ных, используемых в системе.

Функциональную модель целесообразно применять для опре­деления спецификаций программного обеспечения, не предусмат­ривающего работу со сложными структурами данных, так как она ориентирована на декомпозицию функций.

ДИАГРАММЫ ПОТОКОВ ДАННЫХ

Характеристика диаграмм потоков данных (DFD). Диаграмма DFD состоит из узлов обработки данных, средств их хранения и внешних по отношению к используемой диаграмме источников или потребителей данных.

Диаграмма потоков данных — основное средство моделирова­ния функциональных требований к системе, проектируемой или реально существующей. В основе модели лежат понятия внешней сущности, процесса, хранилища (накопителя) данных потока дан­ных. Источники информации (внешние сущности) порождают информационные потоки (потоки данных), переносящие инфор­мацию к подсистемам или процессам; те, в свою очередь, преобра­зуют информацию и порождают новые потоки, которые переносят информацию к другим процессам или подсистемам, накопителям данных или внешним сущностям — потребителям информации.

Для изображения диаграмм потоков данных традиционно ис­пользуют два вида нотаций — Йордана и Гейна—Сарсона, кото­рые представлены в табл. 2.1.

Внешняя сущность — это материальный предмет или физичес­кое лицо, представляющее собой источник или приемник инфор­мации, например, заказчики, персонал, поставщики, клиенты,

Источник

Метод функциональных диаграмм

Метод функциональных диаграмм или диаграмм причинно-следственных связей помогаетсистематически выбирать высокорезультативные тесты. Кроме этого, метод функциональных диаграмм дает полезный побочный эффект, так как позволяет обнаруживать неполноту и неоднозначность исходных спецификаций.

Функциональная диаграмма – это формальный язык, на который транслируется спецификация, написанная на естественном языке.

Методика использования функциональных жиаграмм:

1. Спецификация разбивается на “рабочие” участки, так как для больших спецификаций функциональные диаграммы становятся слишком громоздкими. Например, при тестировании компилятора в качестве рабочего участка можно рассматривать каждый отдельный оператор языка программирования.

2. В спецификации определяются причины и следствия. Причина – это отдельное входное условие или класс эквивалентных входных условий. Следствие – это выходное условие (результат выполнения программы). Например, если при выполнении программы обновляется содержимое некоторого файла, то изменение в нем является результатом выполнения программы, а подтверждающее сообщение – выходным условием.

Причины и следствия определяютсяпутем последовательного чтения спецификации. Каждым причине и следствию приписывается уникальный номер.

3. Анализируется семантическое содержание спецификации, которая преобразуется в булевский граф (функциональную диаграмму), связывающий причины и следствия.

4. Диаграмма дополняетсяпримечаниями, задающими ограничения и описывающими комбинации причин и (или) следствий, которые являются невозможными из-за синтаксических или внешних ограничений.

5. Путем методического прослеживания состояний условий диаграммы она преобразуется в таблицу решений с ограниченными входами. Каждый столбец таблицы решений соответствует тесту.

6. Столбцы таблицы решений преобразуются в тесты.

Процедура генерации таблицы решений заключается в следующем:

a) Выбрать некоторое следствие, которое должно быть в состоянии 1.

b) Найти все комбинации причин (с учетом ограничени), которые установят это следствие в 1, прокладывая из этого следствия обратную трассу через диаграмму.

c) Построить столбец в таблице решений для каждой комбинации причин.

d) Для каждой комбинации причин определить состояния всех других следствий и поместить их в соответствующий столбец таблицы решений.

При выполнении этого шага необходимо руководствоваться следующими положениями:

· Если обратная трасса прокладывается через узел ИЛИ, выход которого должен принимать значение 1, то одновременно не следует устанавливать в 1 более одного входа в этот узел. Цель данного правила – избежать пропуска определенных ошибок из-за того, что одна причина маскируется другой.

· Если обратная трасса прокладывается через узел ИЛИ, выход которого должен принимать значение 0, то все комбинации входов, приводящие выход в 0, должны быть в конечном счете перечислены. Однако, когда исследуется ситуация, где один вход есть 0, а один или более других входов есть 1, не обязательно перечислять все условия, при которых остальные входы могут быть 1.

· Если обратная трасса прокладывается через узел И, выход которого должен принимать значение 0, то необходимо указать лишь одно условие, согласно которому все входы являются нулями.

Каждый узел диаграммы может находиться в двух состояниях – 0 или 1; 0обозначает состояние “отсутствует”, а 1 – “присутствует”.

Для представления функциональных диаграмм используются следующие базовые символы:

Если значение aесть 1, то и значение bесть 1; в противном случае значениеbесть0.

Если значение aесть 0, то значение bесть 1; в противном случае значениеbесть0.

ФункцияИЛИустанавливает, что если a, или b,

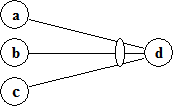
или сесть 1, тоdесть 1; в противном случае dесть 0.

Функция И устанавливает, что если и a, и b есть 1, то и с есть 1; в противном случае сесть 0.

Рассмотрим диаграмму, отображающую спецификацию: Файл обновляется, если символ в колонке 1 является буквой “A” или “B”, а символ в колонке 2 – цифра. Если первый символ ошибочный, то выдается сообщение X1, а если второй символ не является цифрой – сообщение X2.

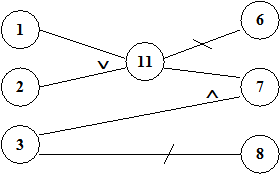
Причины:

1 – символ “A” в колонке 1

2 – символ “B” в колонке 1

3 – цифра в колонке 2

Следствия:

7 – файл обновляется

6 – выдается сообщение X1

8 – выдается сообщение X2

Приведенная функциональная диаграмма содержит невозможную комбинацию причин: причины 1 и 2 не могут быть установлены в 1 одновременно.

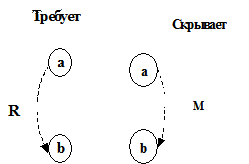
Для изображения невозможных комбинаций причин используются следующие логические ограничения:

Ограничение Е устанавливает, что Е должно быть истинным, если хотя бы одна из причин – а или b – принимает значение 1 (a и b не могут принимать значение 1 одновременно).

Ограничение I устанавливает, что по крайней мере одна из величин a, b или c всегда должна быть равной 1 (a,b и с не могут принимать значение 0 одновременно).

Ограничение О устанавливает, что одна и только одна из величин а или bдолжна быть равна 1.

Ограничение R устанавливает, что если a принимает значение 1, то и b должна принимать значение 1, т.е. невозможно, чтобы a было равно 1, а b – 0.

Ограничение М устанавливает, что если следствие aимеет значение 1, то следствие b должно принять значение 0.

Для рассмотренного выше примера физически невозможно, чтобы причины 1 и 2 присутствовали одновременно, но возможно, чтобы присутствовала одна из них. Следовательно, они связаны ограничением Е.

Преобразуем полученную функциональную диаграмму в таблицу решений.

Выберем следствие 7 (файл обновляется). Следствие 7имеет место, еслиузлы3 и 11есть1. В свою очередь узел 11 есть 1, если одна из причин 1 или 2 имеет значений 1. Таким образом, возможны следующие состояния узлов 1 – 3:

1 0 1 и 0 1 0.

Следствие 6 имеет место, если значение узла 11 есть 0 (узлы1 и 2оба равны 0).

Следствие 8 имеет место, если значение узла 3 есть 0.

Таблица решений будет иметь следующий вид:

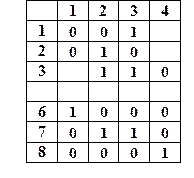
Столбец 1 представляет условие, где следствие 6 есть 1, столбцы 2,3 – следствие 7 есть 1, а столбец 4 соответствует условию, для которого следствие 8 есть 1.

Пробелы в таблице решений представляют “безразличные” ситуации (состояние причины несущественно).

Преобразуем таблицу решений в набор тестов:

Источник