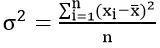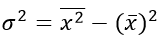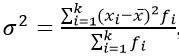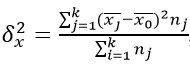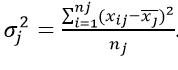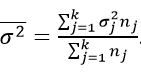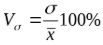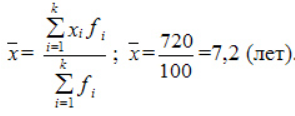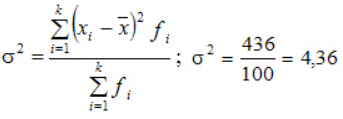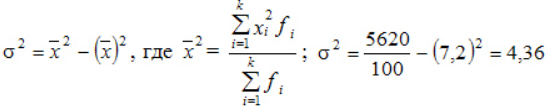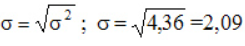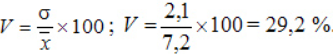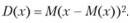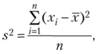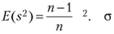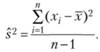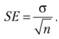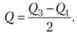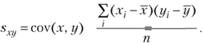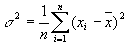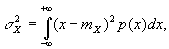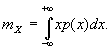Что называют дисперсией что она характеризует

Основы теории вероятностей. Дисперсия случайной величины.

Дисперсия случайной величины характеризует степень разброса случайной величины около ее математического ожидания, то есть её отклонения от математического ожидания.

Если случайная величина ξ имеет математическое ожидание M_ξ, то дисперсией случайной величины ξ выражается так:

Эта универсальная формула отлично применима как для дискретных случайных величин, так и для непрерывных. Величина M_ξ 2 больше для дискретных и непрерывных случайных величин соответственно вычисляется по формулам:

, .

Для вычисления степени разброса значений случайной величины зачастую используют среднеквадратичное отклонение , связанное с дисперсией соотношением .

Свойства дисперсии случайной величины.

Верно и обратное утверждение: если , то почти везде;

,

,

где

Пример. Как найти математическое ожидание и дисперсию.

Предположим, случайная величина X имеет стандартное непрерывное равномерное распределение на [0,1], т.е. её плотность вероятности задана следующим равенством:

Из этого следует, что математическое ожидание квадрата случайной величины можно выразить таким образом:

и формула математического ожидания случайной величины выглядит так:

Следовательно, дисперсию случайной величины найдем по формуле:

.

Источник

Значение слова «дисперсия»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Дисперсия волн — в физике зависимость фазовой скорости волны от её частоты, различают:

Закон дисперсии — в физике закон, выражающий зависимость фазовой скорости волны от её частоты.

Дисперсия случайной величины — одна из усреднённых характеристик случайной величины.

Дисперсия (химия) — образования из двух или более фаз (тел), которые совершенно или практически не смешиваются и не реагируют друг с другом химически

Дисперсия (биология) — термин, обозначающий разнообразие признаков в популяции.

Дисперсия второй вязкости

ДИСПЕ’РСИЯ, и, мн. нет, ж. [латин. dispersio]. 1. Расхождение световых лучей разного цвета при прохождении сквозь преломляющую среду (опт.). 2. Состояние большего или меньшего раздробления вещества (ест.).

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

диспе́рсия

1. матем. стат. разброс чего-либо и численная характеристика такого разброса ◆ Этот старый дурак не сообразил, что существует дисперсия свойств… Стругацкие, «Понедельник начинается в субботу», 1964 г. (цитата из НКРЯ) ◆ В теории вероятностей — дисперсия случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания Владимир Горбачёв, «Концепции современного естествознания», 2003 г. (цитата из НКРЯ)

2. физ. зависимость фазовой скорости волны от частоты ◆ Ещё более крупный шаг в этом направлении был сделан Н. П. Кастериным (1898, 1901, 1904), которому удалось проследить аналогию в явлениях дисперсии акустических и световых волн. П. Н. Лебедев, «Успехи акустики за последние десять лет», 1905 г. (цитата из НКРЯ)

3. физ. характеристика спектрометра, спектроскопа, дифракционной решётки ◆ Только для этого понадобится спектроскоп с очень большой дисперсией, то есть такой спектроскоп, в котором спектр растягивается на очень большую длину. М. П. Бронштейн, «Солнечное вещество», 1936 г. (цитата из НКРЯ)

6. в материаловедении — степень дисперсности, доля атомов в гетерогенной системе, находящихся на границе раздела фаз ◆ Эмульсия с высокой дисперсией.

Источник

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

Пример расчета дисперсии

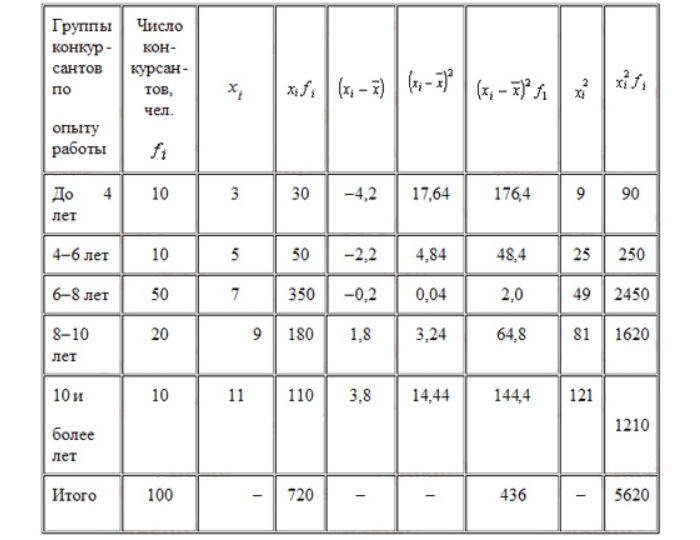
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник

Дисперсия и ее оценка

Определение дисперсии случайных величин

Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.

В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:

где М(х) – математическое ожидание, а D(х) – дисперсия.

На основе данной формулы можно вывести другую, которая дает оценку дисперсии:

В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных. Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.

Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:

Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности. Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения. При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:

Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.

Характеристика оценивания стандартного отклонения

Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением. Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности. Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:

где SE – стандартная ошибка.

Данная статистика необходима для интервальной оценки исследуемой случайной величины.

Характеристика оценки полумежквартильного интервала

Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.

Квартиль – это вариант названия квантиля распределения.

При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:

Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.

Характеристика ковариации

Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:

Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах. Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция». Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.

Источник

Дисперсия

Полезное

Смотреть что такое «Дисперсия» в других словарях:

дисперсия — Рассеяние чего нибудь. В математике дисперсия определяет отклонение величин от среднего значения. Дисперсия белого света приводит к его разложению на составляющие. Дисперсия звука является причиной его расплывания. Рассеяние хранимых данных по… … Справочник технического переводчика

ДИСПЕРСИЯ — (от латинского dispersio рассеяние) волн, зависимость скорости распространения волн в веществе от длины волны (частоты). Дисперсия определяется физическими свойствами той среды, в которой распространяются волны. Например, в вакууме… … Современная энциклопедия

ДИСПЕРСИЯ — (variance) Мера разброса данных. Дисперсия множества из N членов находится путем сложения квадратов их отклонений от среднего значения и деления на N. Поэтому, если членами являются хi при i = 1, 2. N, a их средним является m, дисперсия… … Экономический словарь

Дисперсия — (от латинского dispersio рассеяние) волн, зависимость скорости распространения волн в веществе от длины волны (частоты). Дисперсия определяется физическими свойствами той среды, в которой распространяются волны. Например, в вакууме… … Иллюстрированный энциклопедический словарь

ДИСПЕРСИЯ — (от лат. dispersio рассеяние) в математической статистике и теории вероятностей мера рассеивания (отклонения от среднего). В статистике дисперсия есть среднее арифметическое из квадратов отклонений наблюденных значений (x1, x2. xn) случайной… … Большой Энциклопедический словарь

Дисперсия — в теории вероятностей наиболее употребительная мера отклонения от среднего (мера рассеяния). По английски: Dispersion Синонимы: Статистическая дисперсия Синонимы английские: Statistical dispersion См. также: Выборочные совокупности Финансовый… … Финансовый словарь

ДИСПЕРСИЯ — [лат. dispersus рассеянный, рассыпанный] 1) рассеяние; 2) хим., физ. раздробление вещества на очень малые частицы. Д. света разложение белого света с помощью призмы в спектр; 3) мат. отклонение от среднего. Словарь иностранных слов. Комлев Н.Г.,… … Словарь иностранных слов русского языка

дисперсия — (варианса) показатель разброса данных, соответственный среднему квадрату отклонения этих данных от средней арифметической. Равна квадрату стандартного отклонения. Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998 … Большая психологическая энциклопедия

дисперсия — рассеяние, разброс Словарь русских синонимов. дисперсия сущ., кол во синонимов: 6 • нанодисперсия (1) • … Словарь синонимов

Дисперсия — [variance] характеристика рассеивания значений случайной величины, измеряемая квадратом их отклонений от среднего значения (обозначается d2). Различается Д. теоретического (непрерывного или дискретного) и эмпирического (также непрерывного и… … Экономико-математический словарь

Дисперсия — * дысперсія * dispersion 1. Рассеяние; разброс; вариация (см.). 2. Теоретико вероятностное понятие, характеризующее меру отклонения случайной величины от ее математического ожидания. В биометрической практике используется выборочная дисперсия s2 … Генетика. Энциклопедический словарь

Источник