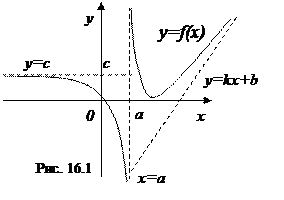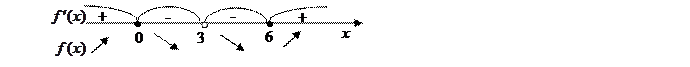Что называют асимптотой кривой

Асимптота

В более общем смысле, одна кривая является криволинейной асимптотой другой (в отличие от линейной асимптоты ), если расстояние между двумя кривыми стремится к нулю, поскольку они стремятся к бесконечности, хотя термин асимптота сам по себе обычно используется для линейных асимптот.

Содержание

Введение [ править ]

Асимптоты функций [ править ]

Вертикальные асимптоты [ править ]

Прямая x = a является вертикальной асимптотой графика функции y = ƒ ( x ), если верно хотя бы одно из следующих утверждений:

Например, если ƒ ( x ) = x / ( x –1), числитель приближается к 1, а знаменатель приближается к 0, когда x приближается к 1. Итак

и кривая имеет вертикальную асимптоту x = 1.

Если функция имеет вертикальную асимптоту, то не обязательно, чтобы производная функции имела вертикальную асимптоту в том же месте. Примером является

lim x → 0 − f ( x ) = lim x → 0 − ( 1 x + sin ⁡ ( 1 x ) ) = − ∞ <\displaystyle \lim _>f(x)=\lim _>\left(<\tfrac <1>>+\sin \left(<\tfrac <1>>\right)\right)=-\infty > .

f ′ ( x ) = − ( cos ⁡ ( 1 x ) + 1 ) x 2 <\displaystyle f'(x)=<\frac <-(\cos(<\tfrac <1>>)+1)>>>> .

Для последовательности точек

Горизонтальные асимптоты [ править ]

Например, функция арктангенса удовлетворяет

У функций могут отсутствовать горизонтальные асимптоты с одной или обеих сторон, либо может быть одна горизонтальная асимптота, одинаковая в обоих направлениях. Например, функция ƒ ( x ) = 1 / ( x 2 +1) имеет горизонтальную асимптоту при y = 0, когда x стремится как к −∞, так и к + ∞, потому что, соответственно,

Наклонные асимптоты [ править ]

В первом случае прямая y = mx + n является наклонной асимптотой ƒ ( x ), когда x стремится к + ∞, а во втором случае прямая y = mx + n является наклонной асимптотой (x), когда x стремится к −∞.

lim x → ± ∞ [ f ( x ) − x ] <\displaystyle \lim _\left[f(x)-x\right]> = lim x → ± ∞ [ ( x + 1 x ) − x ] <\displaystyle =\lim _\left[\left(x+<\frac <1>>\right)-x\right]> = lim x → ± ∞ 1 x = 0. <\displaystyle =\lim _<\frac <1>>=0.>

Элементарные методы определения асимптот [ править ]

Асимптоты многих элементарных функций могут быть найдены без явного использования пределов (хотя при выводе таких методов обычно используются пределы).

Общее вычисление наклонных асимптот для функций [ править ]

m = def lim x → a f ( x ) / x <\displaystyle m<\stackrel <\text><=>>\lim _f(x)/x>

Имея m, значение n может быть вычислено следующим образом:

n = def lim x → a ( f ( x ) − m x ) <\displaystyle n<\stackrel <\text><=>>\lim _(f(x)-mx)>

Например, функция ƒ ( x ) = (2 x 2 + 3 x + 1) / x имеет

m = lim x → + ∞ f ( x ) / x = lim x → + ∞ 2 x 2 + 3 x + 1 x 2 = 2 <\displaystyle m=\lim _f(x)/x=\lim _<\frac <2x^<2>+3x+1>>>=2> а потом n = lim x → + ∞ ( f ( x ) − m x ) = lim x → + ∞ ( 2 x 2 + 3 x + 1 x − 2 x ) = 3 <\displaystyle n=\lim _(f(x)-mx)=\lim _\left(<\frac <2x^<2>+3x+1>>-2x\right)=3>

так что y = 2 x + 3 является асимптотой ƒ ( x ), когда x стремится к + ∞.

Функция ƒ ( x ) = ln x имеет

m = lim x → + ∞ f ( x ) / x = lim x → + ∞ ln ⁡ x x = 0 <\displaystyle m=\lim _f(x)/x=\lim _<\frac <\ln x>>=0> а потом n = lim x → + ∞ ( f ( x ) − m x ) = lim x → + ∞ ln ⁡ x <\displaystyle n=\lim _(f(x)-mx)=\lim _\ln x> , которого не существует.

Поэтому y = ln x не имеет асимптоты, когда x стремится к + ∞.

Асимптоты для рациональных функций [ править ]

Вертикальные асимптоты возникают только тогда, когда знаменатель равен нулю (если и числитель, и знаменатель равны нулю, сравниваются кратности нуля). Например, следующая функция имеет вертикальные асимптоты при x = 0 и x = 1, но не при x = 2.

f ( x ) = x 2 − 5 x + 6 x 3 − 3 x 2 + 2 x = ( x − 2 ) ( x − 3 ) x ( x − 1 ) ( x − 2 ) <\displaystyle f(x)=<\frac -5x+6>-3x^<2>+2x>>=<\frac <(x-2)(x-3)>>>

Наклонные асимптоты рациональных функций [ править ]

f ( x ) = x 2 + x + 1 x + 1 = x + 1 x + 1 <\displaystyle f(x)=<\frac +x+1>>=x+<\frac <1>>>

Преобразования известных функций [ править ]

Если известная функция имеет асимптоту (например, y = 0 для f (x) = e x ), то ее трансляции также имеют асимптоту.

Если известная функция имеет асимптоту, то масштабирование функции также имеет асимптоту.

Общее определение [ править ]

| a x ( t ) + b y ( t ) + c | a 2 + b 2 <\displaystyle <\frac <|ax(t)+by(t)+c|><\sqrt +b^<2>>>>>

| a x ( γ ( t ) ) + b y ( γ ( t ) ) + c | a 2 + b 2 <\displaystyle <\frac <|ax(\gamma (t))+by(\gamma (t))+c|><\sqrt +b^<2>>>>>

которое стремится к нулю одновременно с предыдущим выражением.

Криволинейные асимптоты [ править ]

y = x 3 + 2 x 2 + 3 x + 4 x <\displaystyle y=<\frac +2x^<2>+3x+4>>>

Асимптоты и построение кривых [ править ]

Алгебраические кривые [ править ]

Асимптотический конус [ править ]

x 2 a 2 − y 2 b 2 = 1 <\displaystyle <\frac >>>-<\frac >>>=1>

имеет две асимптоты

Уравнение для объединения этих двух прямых имеет вид

x 2 a 2 − y 2 b 2 = 0. <\displaystyle <\frac >>>-<\frac >>>=0.>

x 2 a 2 − y 2 b 2 − z 2 c 2 = 1 <\displaystyle <\frac >>>-<\frac >>>-<\frac >>>=1>

имеет асимптотический конус [16] [17]

x 2 a 2 − y 2 b 2 − z 2 c 2 = 0. <\displaystyle <\frac >>>-<\frac >>>-<\frac >>>=0.>

Расстояние между гиперболоидом и конусом приближается к 0, когда расстояние от начала координат приближается к бесконечности.

Источник

В более общем смысле, одна кривая является криволинейной асимптотой другой (в отличие от линейной асимптоты ), если расстояние между двумя кривыми стремится к нулю, поскольку они стремятся к бесконечности, хотя термин асимптота сам по себе обычно используется для линейных асимптот.

СОДЕРЖАНИЕ

Вступление

Асимптоты функций

Вертикальные асимптоты

Прямая x = a является вертикальной асимптотой графика функции y = ƒ ( x ), если верно хотя бы одно из следующих утверждений:

Например, если ƒ ( x ) = x / ( x –1), числитель приближается к 1, а знаменатель приближается к 0, когда x приближается к 1. Итак

а кривая имеет вертикальную асимптоту x = 1.

Если функция имеет вертикальную асимптоту, то не обязательно, чтобы производная функции имела вертикальную асимптоту в том же месте. Примером является

Для последовательности точек

Горизонтальные асимптоты

Например, функция арктангенса удовлетворяет

У функций могут отсутствовать горизонтальные асимптоты с одной или обеих сторон, или может быть одна горизонтальная асимптота, одинаковая в обоих направлениях. Например, функция ƒ ( x ) = 1 / ( x 2 +1) имеет горизонтальную асимптоту при y = 0, когда x стремится как к −∞, так и к + ∞, потому что, соответственно,

Наклонные асимптоты

Элементарные методы определения асимптот

Асимптоты многих элементарных функций могут быть найдены без явного использования пределов (хотя при выводе таких методов обычно используются пределы).

Общее вычисление наклонных асимптот для функций

м знак равно def Lim Икс → а ж ( Икс ) / Икс <\ displaystyle m \; <\ stackrel <\ text > <=>> \, \ lim _ f (x) / x>

Имея m, значение n может быть вычислено следующим образом:

Например, функция ƒ ( x ) = (2 x 2 + 3 x + 1) / x имеет

так что y = 2 x + 3 является асимптотой ƒ ( x ), когда x стремится к + ∞.

Функция ƒ ( x ) = ln x имеет

Итак, y = ln x не имеет асимптоты, когда x стремится к + ∞.

Асимптоты для рациональных функций

Вертикальные асимптоты возникают только тогда, когда знаменатель равен нулю (если и числитель, и знаменатель равны нулю, кратности нуля сравниваются). Например, следующая функция имеет вертикальные асимптоты при x = 0 и x = 1, но не при x = 2.

Наклонные асимптоты рациональных функций

Преобразования известных функций

Если известная функция имеет асимптоту (например, y = 0 для f (x) = e x ), то ее трансляции также имеют асимптоту.

Если известная функция имеет асимптоту, то масштабирование функции также имеет асимптоту.

Общее определение

которое стремится к нулю одновременно с предыдущим выражением.

Криволинейные асимптоты

Асимптоты и построение эскизов кривых

Алгебраические кривые

Асимптотический конус

имеет две асимптоты

Уравнение для объединения этих двух прямых имеет вид

имеет асимптотический конус

Расстояние между гиперболоидом и конусом приближается к 0, когда расстояние от начала координат приближается к бесконечности.

Источник

Асимптота

Полезное

Смотреть что такое «Асимптота» в других словарях:

АСИМПТОТА — (от греч. a отриц. част., и symptotos совпадающий вместе). Прямая линия, постоянно приближающаяся к кривой и встречающаяся с ней только в бесконечности. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АСИМПТОТА от… … Словарь иностранных слов русского языка

АСИМПТОТА — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы … Современная энциклопедия

АСИМПТОТА — (от греч. asymptotos несовпадающий) кривой с бесконечной ветвью прямая, к которой эта ветвь неограниченно приближается, напр., асимптота гиперболы … Большой Энциклопедический словарь

асимптота — Прямая линия, к которой постепенно приближается кривая. [http://www.morepc.ru/dict/] асимптота Прямая, к которой стремится (никогда не достигая ее) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или … Справочник технического переводчика

Асимптота — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы. … Иллюстрированный энциклопедический словарь

АСИМПТОТА — жен., геом. прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся. Пример, для объяснения этого: если какое либо число все делить пополам, то оно будет умаляться до бесконечности, но никогда не сделается нулем.… … Толковый словарь Даля

асимптота — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Асимптота — (от греч. слов: a, sun, piptw) несовпадающая. Подасимптотой подразумевается такая линия, которая, будучи неопределеннопродолжена, приближается к данной кривой линии или к некоторой ее частитак, что расстояние между общими линиями делается менее… … Энциклопедия Брокгауза и Ефрона

Асимптота — поверхности называется прямая линия, пересекающаяповерхность по крайней мере в двух бесконечно удаленных точках … Энциклопедия Брокгауза и Ефрона

АСИМПТОТА — (asymptote) Значение, к которому стремится данная функция при изменении аргумента (argument), но не достигает его ни при одном конечном значении аргумента. Например, если общая стоимость выпуска х задается функцией ТС=а+bх, где а и b – константы … Экономический словарь

Асимптота — [asymptote] прямая, к которой стремится (никогда не достигая ее), имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или уменьшается. Например, в функции: y = c + 1/x значение y приближается с… … Экономико-математический словарь

Источник

АСИМПТОТА КРИВОЙ

АСИМПТОТА КРИВОЙ — прямая линия, которую никогда не может пересечь или с нею слиться неограниченно приближающаяся к ней некоторая кривая; напр. гипербола имеет своими асимптотами оси координат.

Смотреть что такое «АСИМПТОТА КРИВОЙ» в других словарях:

Асимптота кривой — (от греч. asymptotos не сливающаяся) прямая, к которой приближается как угодно близко точка кривой при удалении в бесконечность … Начала современного естествознания

Асимптота (значения) — Асимптота кривой с бесконечной ветвью прямая, к которой эта ветвь неограниченно приближается. Asymptote язык описания векторной графики, дополняющий функциональность LaTeX … Википедия

АСИМПТОТА — (от греч. a отриц. част., и symptotos совпадающий вместе). Прямая линия, постоянно приближающаяся к кривой и встречающаяся с ней только в бесконечности. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АСИМПТОТА от… … Словарь иностранных слов русского языка

Асимптота — (от греч. слов: a, sun, piptw) несовпадающая. Подасимптотой подразумевается такая линия, которая, будучи неопределеннопродолжена, приближается к данной кривой линии или к некоторой ее частитак, что расстояние между общими линиями делается менее… … Энциклопедия Брокгауза и Ефрона

АСИМПТОТА — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы … Современная энциклопедия

АСИМПТОТА — (от греч. asymptotos несовпадающий) кривой с бесконечной ветвью прямая, к которой эта ветвь неограниченно приближается, напр., асимптота гиперболы … Большой Энциклопедический словарь

Асимптота — (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы. … Иллюстрированный энциклопедический словарь

АСИМПТОТА — жен., геом. прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся. Пример, для объяснения этого: если какое либо число все делить пополам, то оно будет умаляться до бесконечности, но никогда не сделается нулем.… … Толковый словарь Даля

Источник

Лекция 16. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ

План:

Одним из важных этапов построения графиков функций является поиск асимптот. С асимптотами мы встречались неоднократно: при построении графиков функций 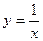, y=tgx, y=сtgx. Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.

Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная. На чертеже асимптоты принято обозначать пунктирными линиями.

Рассмотрим следующий искусственно составленный график функции (рис. 16.1), на примере которого хорошо видны все виды асимптот:

Дадим определение каждому виду асимптот:

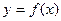
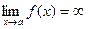
1. Прямая х=а называется вертикальной асимптотой функции , если .

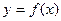
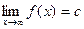
2. Прямая у=с называется горизонтальной асимптотой функции , если .

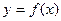
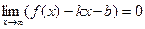
3. Прямая у=kx+b называется наклонной асимптотой функции , если .

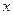
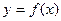
Геометрически определение наклонной асимптоты означает, что при →∞ график функции сколь угодно близко подходит к прямой у=kx+b, т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.

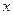
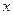
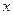
Отметим, что горизонтальные и наклонные асимптоты рассматриваются только при условии →∞. Иногда их различают на горизонтальные и наклонные асимптоты при →+∞ и →-∞.

Для поиска асимптот можно использовать следующий алгоритм:

Вертикальных асимптот может быть одна, несколько или не быть совсем.

Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем – их нет.

Рассмотрим примеры нахождения асимптот функции:

Пример 16.1. Найдите асимптоты кривой .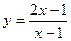

Решение. 1. Найдем область определения функции: х-1≠0; х≠1.

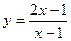
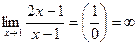
Проверим, является ли прямая х=1 вертикальной асимптотой. Для этого вычислим предел функции в точке х=1: .

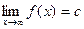
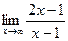
2. Для поиска горизонтальных асимптот находим : с= .

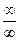
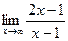
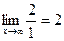
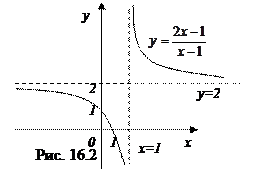
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с= = . Т.к. с=2 (число), то у=2 – горизонтальная асимптота.

Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.

Таким образом, данная функция имеет вертикальную асимптоту х=1 и горизонтальную асимптоту у=2. Для наглядности график данной функции представлен на рис. 16.2.

Пример 16.2. Найдите асимптоты кривой .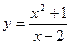

Решение. 1. Найдем область определения функции: х-2≠0; х≠2.

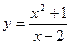
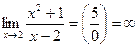
Проверим, является ли прямая х=2 вертикальной асимптотой. Для этого вычислим предел функции в точке х=2: .

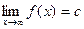
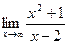
2. Для поиска горизонтальных асимптот находим : с= .

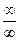
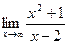
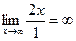
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с= = . Т.к. с – бесконечность, то горизонтальных асимптот нет.

3. Для поиска наклонных асимптот находим :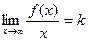

= = = .

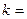
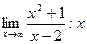
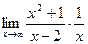
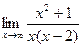
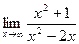
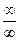
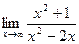
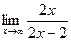
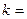
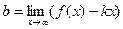
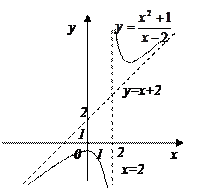
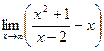
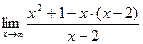
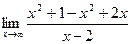
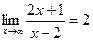
Получили неопределенность вида , воспользуемся правилом Лопиталя: = =1.Итак, 1. Найдем b по формуле: .

b= = =

= = .

Получили, что b= 2. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+2.

Таким образом, данная функция имеет вертикальную асимптоту х=2 и наклонную асимптоту у=x+2. Для наглядности график функции 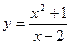представлен на рис. 16.3.

Контрольные вопросы:

Лекция 17. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ГРАФИКА

В данной лекции мы подведем итог всему ранее изученному материалу. Конечная цель нашего долгого пути – уметь исследовать любую аналитически заданную функцию и строить ее график. Важными звеньями нашего исследования будут исследование функции на экстремумы, определение интервалов монотонности, выпуклости и вогнутости графика, поиск точек перегиба, асимптот графика функции.

С учетом всех вышеперечисленных аспектов приведем схему исследования функции и построения графика.

1. Найти область определения функции.

2. Исследовать функцию на четность-нечетность:

· если 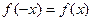, то функция четная (график четной функции симметричен относительно оси Оу);

· если 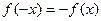, то функция нечетная (график нечетной функции симметричен относительно начала координат);

· в противном случае функция ни четная, ни нечетная.

3. Исследовать функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).

4. Найти точки пересечения графика функции с осями координат:

· Ох: у=0 (решаем уравнение лишь в том случае, если можем использовать известные нам методы);

5. Найти первую производную функции и критические точки первого рода.

6. Найти интервалы монотонности и экстремумы функции.

7. Найти вторую производную функции и критические точки второго рода.

8. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.

9. Найти асимптоты графика функции.

10. Построить график функции. При построении следует учесть случаи возможного расположения графика вблизи асимптот:

вертикальной	горизонтальной	наклонной

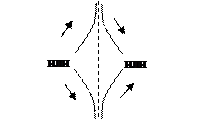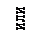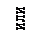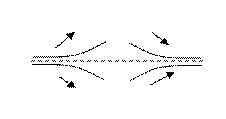11. При необходимости выбрать контрольные точки для более точного построения.

Рассмотрим схему исследования функции и построения ее графика на конкретных примерах:

Пример 17.1. Постройте график функции .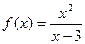

Решение. 1. Данная функция определена на всей числовой прямой за исключением х=3, т.к. в этой точке знаменатель обращается в ноль.

2. Для определения четности и нечетности функции найдем :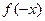

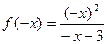
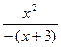
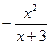
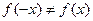
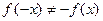
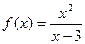
= = . Видим, что и , следовательно, функция ни четная, ни нечетная.

3. Функция непериодическая.

4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у=0. Получим уравнение: 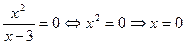. Итак, точка (0; 0) – точка пересечения с осями координат.

5. Найдем производную функции по правилу дифференцирования дроби: = = = = .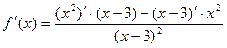

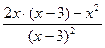
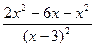
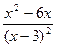
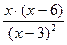
Для нахождения критических точек найдем точки, в которых производная функции равна 0 или не существует.

, если =0, следовательно, . Произведение тогда равно 0, когда хотя бы один из множителей равен 0: или .

не существует, если знаменатель (х-3) 2 равен 0, т.е. не существует при х=3.

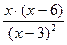
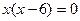
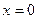
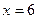
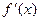
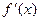
Итак, функция имеет три критические точки первого рода: ; ; .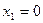

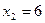
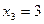
6. На числовой оси отметим критические точки первого рода, причем точку 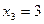отмечаем выколотой точкой, т.к. в ней функция не определена.

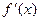
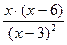
Расставляем знаки производной = на каждом промежутке:

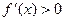
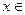
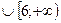
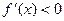
На промежутках, где , исходная функция возрастает (при (-∞;0] ), где — убывает (при [0;3) (3;6]).

Точка х=0 является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: .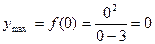

Точка х=6 является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: .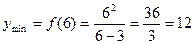

Результаты исследований можно занести в таблицу. Число строк в таблице фиксировано и равно четырем, а число столбцов зависит от исследуемой функции. В ячейки первой строки последовательно заносят интервалы, на которые критические точки разбивают область определения функции, включая сами критические точки. Во избежание ошибок при построении точки, не принадлежащие области определения, можно в таблицу не включать.

Во второй строке таблицы расставляются знаки производной на каждом из рассматриваемых промежутков и значение производной в критических точках. В соответствии со знаками производной функции в третьей строке отмечаются промежутки возрастания, убывания, экстремумы функции.

Последняя строка служит для обозначения максимума и минимума функции.

х	(-∞;0)	(0;3)	(3;6)	(6;+ ∞)
	+	—	—	+
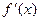f(x)
Выводы	max	min

7. Найдем вторую производную функции как производную от первой производной: = =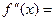

= .

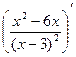
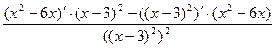
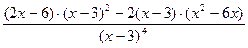
Вынесем в числителе х-3 за скобки и выполним сокращение:

= .

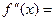
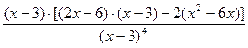
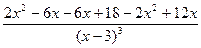
Приведем в числителе подобные слагаемые: .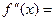

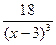
Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.

0, если =0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.

не существует, если знаменатель (х-3) 3 равен 0, т.е. не существует при х=3.

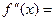
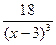
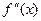
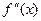
Итак, функция имеет одну критическую точку второго рода: .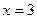

8. Найдем интервалы выпуклости и точки перегиба графика функции.

На числовой оси отметим критическую точку второго рода выколотой точкой, т.к. в ней функция не определена.

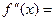
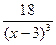
Расставляем знаки второй производной на каждом промежутке:

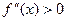
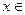
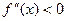
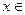
На промежутках, где , исходная функция вогнута (при (3;+∞)), где — выпукла (при (-∞;3)).

Точка х=3 не является точкой перегиба графика функции, т.к. в ней исходная функция не определена.

9. Найдем асимптоты графика функции.

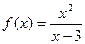
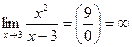
9.1. Поскольку область определения функции – все действительные числа за исключением х=3, то проверим, является ли прямая х=3 вертикальной асимптотой. Для этого вычислим предел функции в точке х=3: .

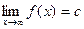
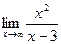
9.2. Для поиска горизонтальных асимптот находим : с= .

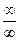
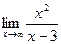
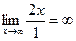
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с= = . Т.к. с – бесконечность, то горизонтальных асимптот нет.

9.3. Для поиска наклонных асимптот находим :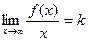

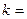
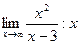
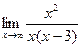
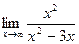
= = =1.

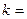
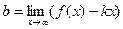
Итак, 1. Найдем b по формуле: .

b= = = = .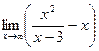

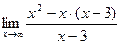
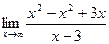
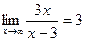
Получили, что b= 3. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+3.

Таким образом, данная функция имеет вертикальную асимптоту х=3 и наклонную асимптоту у=x+3.

10. По полученным ранее данным строим график функции (рис. 17.1). Поскольку к построению графика предъявляются высокие требования, система координат должна быть задана корректно: должно присутствовать обозначение осей Ох, Оу, начало отсчета, единицы измерения по каждой оси.

Прежде чем строить график функции, нужно:

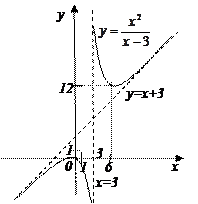
· провести асимптоты пунктирными линиями;

· отметить точки пересечения с осями координат;

·

отметить максимум и минимум функции, причем рекомендуется прямо на чертеже обозначить максимум и минимум функции дугами: k или ;

· пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построить график функции. Ветви графика должны «стремиться» к асимптотам, но их не пересекать.

· проверить, соответствует ли график функции проведенному исследованию: если функция четная или нечетная, то соблюдена ли симметрия; соответствуют ли теоретически найденным промежутки возрастания и убывания, выпуклости и вогнутости, точки перегиба.

; .

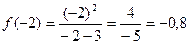
Корректируем график с учетом контрольных точек.

Контрольные вопросы:

ГЛАВА 3. 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник