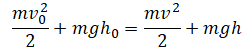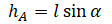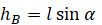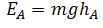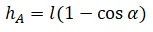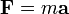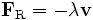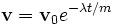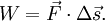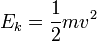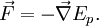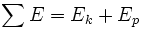Что называется замкнутой механической системой
Большая Энциклопедия Нефти и Газа
Замкнутая механическая система
Замкнутая механическая система состоит из двух произвольно движущихся частиц, заряды которых е и е2, а массы т и т2 соответственно. Доказать, что если начало координат выбрано в центре инерции, то магнитный JUL и механический М моменты системы пропорциональны друг другу, и найти коэффициент пропорциональности. [1]
Замкнутой механической системой точек мы называем такую систему, в которой движение частиц обусловлено только силами взаимодействия, или внутренними силами. [2]
Импульс замкнутой механической системы имеет различные значения по отношению к различным ( инерциальным) системам отсчета. [3]
Энергия замкнутой механической системы Е ( Р, Q) может дополнительно зависеть от заданных внешних параметров А, характеризующих, например, форму и размеры занимаемого системой объема. Согласно определению свободной энергии (1.4.3) она также должна зависеть от этих параметров наравне с зависимостью от температуры. [4]
Для замкнутой механической системы внешние силы отсутствуют, поэтому для замкнутых систем выполняется закон сохранения импульса. Поэтому центр масс и называют иначе центром инерции. [5]
Для замкнутой механической системы условие равенства нулю суммы моментов всех внешних сил, действующих на систему, всегда выполнено. Следовательно, если движение системы происходит под действием только внутренних сил, то вектор кинетического момента остается постоянным по величине и направлению во все время движения. [6]
В замкнутой механической системе сумма механических видов энергии ( потенциальной и кинетической энергии, включая энергию вращательного движения) остается неизменной. [8]
В замкнутых механических системах при любых взаимодействиях частиц полный импульс системы сохраняется независимо от того, будут ли внутренние силы потенциальными или непотенциальными. [9]
Трущиеся тела являются элементами замкнутой механической системы со многими степенями свободы. Помимо заданного относительного движения тела могут иметь другие относительные движения в соответствии со степенями свободы. Такими движениями могут быть следующие: движение в нормальном направлении к поверхности скольжения; движение в плоскости скольжения, но в направлении, перпендикулярном заданному; повороты тел около той или иной координатной оси. [12]
Как хорошо известно, в замкнутой механической системе строгими аддитивными интегралами движения являются масса, импульс и энергия. Мы не включаем сюда момент вращения, поскольку для систем с бесструктурными частицами ( взаимодействующими центрально) закон сохранения момента вращения выполняется автоматически. [13]
Это, в частности, значит, что поворот замкнутой механической системы как целого ( без нарушения условий ее существования) не повлияет на дальнейший ход физических процессов в ней. [14]
Это, в частности, означает, что при поступательном перемещении замкнутой механической системы из одного места в другое ( без нарушения условий ее существования) ход физических процессов в ней не изменится. [15]
Закон сохранения механической энергии
теория по физике 🧲 законы сохранения
В механике все силы делятся на две группы: консервативные и неконсервативные.
Консервативными, или потенциальными, называются такие силы, работа которых не зависит от траектории, а определяется только начальным и конечным положениями тела. Работа таких сил по перемещению тела по замкнутой траектории всегда равна нулю. Примеры потенциальных (консервативных) сил:
Неконсервативными называются такие силы, работа которых зависит от траектории. Сама сила в этом случае зависит от модуля и направления вектора скорости. Работа таких сил может приводить к выделению тепла — часть механической энергии при этом превращается в тепловую. Примеры неконсервативных сил:
Полная механическая энергия — это сумма потенциальной и кинетической энергии тела в определенный момент времени:
Закон сохранения механической энергии
В замкнутой системе, в которой действуют консервативные силы, механическая энергия сохраняется.
Замкнутая система — это система, в которой тела, входящие в нее, взаимодействуют только друг с другом, а влиянием внешних сил можно пренебречь.
Согласно закону сохранения энергии, сумма потенциальной и кинетической энергии системы до взаимодействия тел равна сумме потенциальной и кинетической энергий системы после их взаимодействия:
Закон сохранения механической энергии для движения в поле тяжести Земли
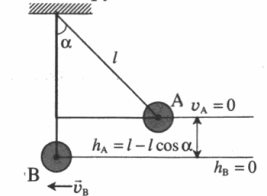
Примеры определения полной механической энергии в начальном и конечном положении
| Пример | Полная механическая энергия в начальной точке (А) | Полная механическая энергия в конечной точке (В) |
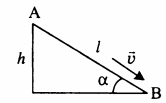
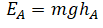 Высоту, на которой изначально находилось тело, можно рассчитать по формуле: | 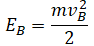 | |
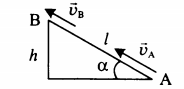
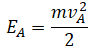 | 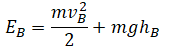 Высоту, на которую поднялось тело, можно рассчитать по формуле: | |
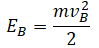 | ||
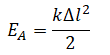 | 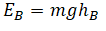 |
Пример №1. Камень брошен вертикально вверх. В момент броска он имел кинетическую энергию, равную 30 Дж. Какую потенциальную энергию относительно поверхности земли будет иметь камень в верхней точке траектории полета? Сопротивлением воздуха пренебречь.
Так как это условно замкнутая система (сопротивлением воздуха мы пренебрегаем), мы можем применить закон сохранения энергии:
Учтем, что в момент броска камень находился на поверхности земли. Поэтому он обладал максимальной кинетической энергией и нулевой потенциальной. Но в верхней точке траектории его скорость стала равна нулю. Поэтому его кинетическая энергия тоже стала равна нулю. Зато потенциальная энергия в этой точке возросла до максимума. Поэтому:
Следовательно, потенциальная энергия в верхней точки траектории полета равна 30 Дж.
Алгоритм решения
Решение
Запишем исходные данные:
Закон сохранения механической энергии для замкнутой системы:
Согласно условию задачи, система не является замкнутой, так как на шарик действует сила сопротивления воздуха. Поэтому закон сохранения энергии примет вид:
Шарик начал падать из состояния покоя, поэтому начальная кинетическая энергия равна нулю. В момент приземления кинетическая энергия максимальная, а потенциальная равна нулю. Поэтому:
Потенциальная энергия определяется формулой:
Отсюда кинетическая энергия шарика в момент перед падением на землю равна:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Запишем закон сохранения механической энергии:
Полная механическая энергия тела равна:
Исходя из закона, сумма потенциальной и кинетической энергии в начальный момент движения тела равно сумме потенциальной и кинетической энергии в конечный момент времени:
Так как полная механическая энергия не меняется с течением времени, ее графиком должна быть прямая, параллельная оси времени. Поэтому верный ответ — а.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Тело, брошенное вертикально вверх от поверхности Земли, достигло максимальной высоты 20 м. С какой начальной скоростью тело было брошено вверх? Сопротивлением воздуха пренебречь.
ЗАМКНУТАЯ СИСТЕМА
Смотреть что такое «ЗАМКНУТАЯ СИСТЕМА» в других словарях:
замкнутая система — [среда] применения (штриховое кодирование): Система [среда] с применением штрихового кодирования, предназначенная для использования обособленной группой пользователей. Примечание Обычно такая система представляет собой группу пользователей в… … Словарь-справочник терминов нормативно-технической документации
Замкнутая система — (генная инженерия) в генной инженерии система осуществления генно инженерной деятельности, при которой генетические модификации вносятся в организм или генно инженерно модифицированные организмы, обрабатываются, культивируются, хранятся,… … Википедия
замкнутая система — система с обратной связью — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] замкнутая система закрытая система Система, изолированная от внешней среды. Конечно,… … Справочник технического переводчика
ЗАМКНУТАЯ СИСТЕМА — см. Система экологическая замкнутая. Экологический энциклопедический словарь. Кишинев: Главная редакция Молдавской советской энциклопедии. И.И. Дедю. 1989 … Экологический словарь
ЗАМКНУТАЯ СИСТЕМА — ЗАМКНУТАЯ СИСТЕМА, то же, что изолированная система (см. ИЗОЛИРОВАННАЯ СИСТЕМА) … Энциклопедический словарь
ЗАМКНУТАЯ СИСТЕМА — (1) в механике система тел, на которые не действуют внешние силы, т. е. силы, приложенные со стороны других, не входящих в рассматриваемую систему тел; (2) в термодинамике система тел, которая не обменивается с внешней средой ни энергией, ни… … Большая политехническая энциклопедия
ЗАМКНУТАЯ СИСТЕМА — то же, что изолированная система. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
ЗАМКНУТАЯ СИСТЕМА — элементов, замкнутая система функций, система элементов jn некоторого линейного нормированного пространства Нтакая, что любой элемент можно сколь угодно точно приблизить в метрике пространства Нконечной линейной комбинацией элементов из этой… … Математическая энциклопедия
замкнутая система — uždaroji sistema statusas T sritis Standartizacija ir metrologija apibrėžtis Termodinaminė sistema, kuri su aplinka arba kitomis sistemomis nesikeičia medžiaga. atitikmenys: angl. closed system vok. geschlossenes System, n; System mit Rückführung … Penkiakalbis aiškinamasis metrologijos terminų žodynas
замкнутая система — uždaroji sistema statusas T sritis chemija apibrėžtis Termodinaminė sistema, kuri nesikeičia medžiaga su aplinka. atitikmenys: angl. closed system rus. закрытая система; замкнутая система … Chemijos terminų aiškinamasis žodynas
замкнутая система — uždaroji sistema statusas T sritis fizika atitikmenys: angl. closed system vok. abgeschlossenes System, n; geschlossenes System, n rus. замкнутая система, f pranc. système fermé, m … Fizikos terminų žodynas
Механическая система
| Фундаментальные понятия |
|---|
| Пространство · Время · Масса · Сила Энергия · Импульс |
| Формулировки |
|---|
| Ньютоновская механика Лагранжева механика Гамильтонова механика |
| Разделы |
|---|
| Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика |
| Учёные |
|---|
| Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши |
Класси́ческая меха́ника — вид механики (раздела физики, изучающей законы изменения положений тел и причины, это вызывающие), основанный на 3 законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «Ньютоновской механикой». Важное место в классической механике занимает существование инерциальных систем. Классическая механика подразделяется на кинематику (которая изучает геометрическое свойство движения без рассмотрения его причин), статику (которая рассматривает равновесие тел) и динамику (которая рассматривает движение тел).
Классическая механика дает очень точные результаты в рамках повседневного опыта. Но для систем, движущихся с большими скоростями, приближающимися к скорости света, более точные результаты дает релятивистская механика, для систем микроскопических размеров — квантовая механика, а для систем, обладающих обеими характеристиками — квантовая теория поля. Тем не менее, классическая механика сохраняет свое значение, поскольку (1) она намного проще в понимании и использовании, чем остальные теории, и (2) в обширном диапазоне она достаточно хорошо приближается к реальности. Классическую механику можно использовать для описания движения таких объектов, как волчок и бейсбольный мяч, многих астрономических объектов (таких, как планеты и галактики), и даже многих микроскопических объектов, таких как органические молекулы.
Хотя классическая механика в общих чертах совместима с другими «классическими теориями», такими как классическая электродинамика и термодинамика, в конце 19 века были найдены несоответствия, которые удалось разрешить только в рамках более современных физических теорий. В частности, классическая электродинамика предсказывает, что скорость света постоянна для всех наблюдателей, что трудно совместить с классической механикой, и что привело к необходимости создания специальной теории относительности. При рассмотрении совместно с классической термодинамикой, классическая механика приводит к парадоксу Гиббса в котором невозможно точно определить величину энтропии и к ультрафиолетовой катастрофе, в которой абсолютно чёрное тело должно излучать бесконечное количество энергии. Попытки разрешить эти проблемы привели к развитию квантовой механики.
Содержание
Описание теории
Перейдем к изложению основных понятий классической механики. Для простоты, мы будем рассматривать только материальную точку, т. е. тело, размером которого можно пренебречь. Движение материальной точки характеризуется несколькими параметрами: её положением, массой, и приложенными к ней силами. Рассмотрим каждый из них по очереди.
В действительности, любое тело, которое подчиняется законам классической механики, обязательно имеет ненулевой размер. Настоящие материальные точки, такие, как электрон, подчиняются законам квантовой механики. Тела ненулевого размера могут испытывать более сложные движения, поскольку может меняться их внутренняя конфигурация, например, потому что теннисный мяч может двигаться, вращаясь. Тем не менее, мы сможем применить к подобным телам результаты, полученные для материальных точек, рассматривая такие тела, как совокупности большого количества взаимодействующих материальных точек. Мы сможем показать, что такие сложные тела ведут себя, как материальные точки, при условии, что они малы в масштабах рассматриваемой задачи.
Радиус-вектор и его производные
Радиус-вектор материальной точки указывает на её положение по отношению к произвольной точке, зафиксированной в пространстве, которая обычно называется началом координат, и обозначается O. Это вектор r соединяющий начало координат с частицей. В общем случае, материальная точка движется, поэтому r является функцией t, промежутка времени прошедшего с произвольного начального момента. Скорость изменения положения со временем, определяется так:
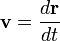
Ускорение, или скорость изменения скорости, это:
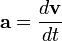
Вектор ускорения может меняться за счет изменения его направления, величины, или и того и другого. Если скорость уменьшается, иногда пользуются термином «замедление», но вообще, термин «ускорение» относится к любому изменению скорости.
Второй закон Ньютона
Второй закон Ньютона связывает массу и скорость частицы с векторной величиной, известной как сила. Пусть m — масса тела и F — векторная сумма всех приложенных к нему сил (то есть равнодействующая сила.) Тогда второй закон Ньютона выглядит так:
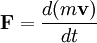
Величина mv называется импульсом. В большинстве случаев, масса m не изменяется со временем, и закон Ньютона можно записать в упрощенной форме
где a — ускорение, определенное выше. Не всегда выполняется условие независимости массы от времени. Например, масса ракеты уменьшается по мере использования горючего. В таких случаях последнее выражение неприменимо, и следует пользоваться полной формой второго закона Ньютона.
Второго закона Ньютона недостаточно для описания движения частицы. Дополнительно требуется описание силы F, полученное из рассмотрения сущности физического взаимодействия, в котором участвует тело. Например, сила трения может быть смоделирована как функция скорости частицы, а именно
где λ — некоторая положительная постоянная. Получив независимое выражение для каждой силы, действующей на тело, мы можем подставить его во второй закон Ньютона и получим дифференциальное уравнение, называемое уравнением движения. Продолжая наш пример, примем, что на тело действует только сила трения. Тогда уравнение движения будет иметь вид
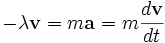
Это можно интегрировать, что даст
где v0 — начальная скорость. Это означает, что скорость тела экспоненциально уменьшается со временем до нуля. Проинтегрировав последнее выражение, мы можем получить радиус-вектор r тела, как функцию времени.
Важными силами являются сила всемирного тяготения и сила Лоренца для электромагнетизма. Помимо этого, для определения сил, действующих на тело, используется третий закон Ньютона: если мы знаем, что тело A действует с силой F на тело B, значит B должно действовать с равной по величине и противоположной по направлению силой реакции, −F, на A.
Энергия
Если сила 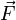
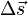
Если масса частицы постоянна, а Wtotal полная работа, совершенная частицей, определяемая как сумма работ совершенных приложенными к частице силами, то второй закон Ньютона примет вид:
где Ek называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до скорости v :
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Если все силы, действующие на частицу консервативны, и Ep является полной потенциальной энергий, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:
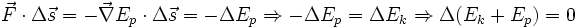 . . |
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
является постоянной относительно времени. Это очень полезно, потому что часто приходится сталкиваться с консервативными силами.
Закон сохранения импульса, кинетическая и потенциальные энергии, мощность силы
Теория к заданию 3 из ЕГЭ по физике
Импульс тела
Импульсом тела называется величина, равная произведению массы тела на его скорость.
Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:
Направление вектора импульса всегда совпадает с направлением скорости.
Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:
Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.
Импульс системы тел. Закон изменения импульса
Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
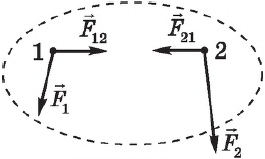
Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.
Закон сохранения импульса
Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.
Закон сохранения импульса гласит:
Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.
Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.
Реактивное движение
Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.
Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.
Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.
Отсюда следует, что скорость ракеты
Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.
Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.
Работа силы
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством: