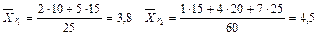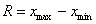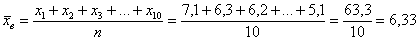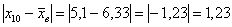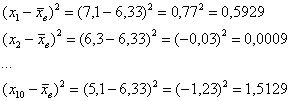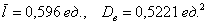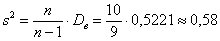Что называется выборочной дисперсией отдельного результата

Как вычислить выборочную дисперсию

Выборочная дисперсия, описание

Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.

Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).

Связь выборочной и генеральной дисперсии

Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.

Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.

Как вычислить выборочную дисперсию

Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:

Для значений признаков выборочной совокупности с частотами n₁, n₂,…,n_k формула выглядит следующим образом:

Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:

Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:

Если вариационный ряд выборочной совокупности интервальный, то за x_i принимается центр частичных интервалов.

Пример

Найти выборочную дисперсию выборки со значениями:

Решение

Для начала необходимо определить выборочную среднюю:

Затем найдем выборочную дисперсию:

Исправленная дисперсия

Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:

В данной формуле D_Г – это истинное значение дисперсии генеральной совокупности.

Исправить выборочную дисперсию можно путем умножения ее на дробь:

Получим формулу следующего вида:

Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:

При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.

Для чего применяют исправленную выборочную дисперсию

Исправленную выборочную используют для точечной оценки генеральной дисперсии.

Пример

Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.

Источник

Выборочная несмещенная дисперсия

Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».

Понятие о сплошном и выборочном наблюдении

С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.

Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.

Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.

В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.

Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.

У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.

Выборочная несмещенная дисперсия

И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?

Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.

Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.

Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.

Отклонение выборочной средней от генеральной показано на рисунке.

Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.

Выборочная смещенная дисперсия:

Выборочная несмещенная дисперсия:

Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.

Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.

Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.

При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.

Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.

Из данной статьи неплохо бы усвоить следующее.

1. Формула генеральной дисперсии в выборке дает смещенную оценку.

2. В знаменателе несмещенной оценки n-1 вместо n.

3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.

4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.

Источник

Выборочная средняя и выборочная дисперсия

Пусть для изучения генеральной совокупности относительно количественного признака Х произведена выборка объёма n.

Выборочной средней называется среднее арифметическое значение выборки.

Если все значения х₁, х₂, …, х_n выборки различны, то

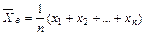(7.1)

(7.2)

Иногда бывает целесообразным выборочные значения случайной величины разбить на отдельные группы. Для каждой группы можно найти её среднюю.

Групповой средней называется среднее арифметическое значений выборки, принадлежащих группе.

По групповым средним можно найти среднее для всей выборки.

Общей средней называется среднее арифметическое значение групповых средних.

Пример 7.1.Найти общую среднюю на основе выборки.

Решение: Находим групповые средние:

Если варианты х_i – большие числа, то для облегчения вычисления выборочной средней используют следующий приём. Пусть С – константа.

, то формула (7.1) преобразуется к виду:

(7.3)

Пример 7.2.Имеется выборка:

Найти выборочную среднюю.

Решение: Берем С=72 и вычисляем разности

Их сумма: α₁+α₂+…+α₁₀=-0,38; их среднее арифметическое: ; выборочная средняя: .

Для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки относительно выборочного среднего вводят понятие выборочной дисперсии.

Выборочной дисперсией D_в называется среднее арифметическое квадратов отклонений наблюдаемых значений признака Х от выборочной средней .

Если все значения х₁, х₂, …, х_n признака выборки объёма n различны, то

(7.4)

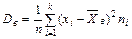(7.5)

Пример 7.3.Выборочная совокупность задана таблицей распределения:

Найти выборочную дисперсию.

Решение: Согласно формулам (7.2) и (7.5) имеем:

.

Выборочным средним квадратическим отклонением называется квадратный корень из выборочной дисперсии:

Можно доказать, что

(7.6)

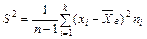(7.7)

Исправленная дисперсия (7.7) является несмещенной оценкой генеральной дисперсии

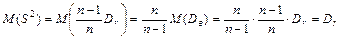Если варианты х_i – большие числа, то для облегчения вычисления выборочной дисперсии D_в формулу (7.4) преобразуют к следующему виду:

(7.8)

где С – ложный нуль.

Пример 7.4.Через каждый час измерялось напряжение тока в электросети. Результаты измерений в вольтах представлены в таблице 7.1:

Найти оценки для математического ожидания и дисперсии результатов измерений.

Решение: Оценки для математического ожидания и дисперсии найдем по формулам (7.3) и (7.8), положив С=220. Все необходимые вычисления приведены в таблице 7.2:

Источник

5. Размах вариации. Среднее линейное отклонение.
Генеральная и выборочная дисперсия

На предыдущем уроке по математической статистике мы изучили центральные показатели статистической совокупности, а именно моду, медиану, среднюю, и теперь переходим к показателям вариации. Они показывают, КАК варьируются статистические данные, а именно – насколько далеко «разбросаны» варианты относительно средних значений, да и просто друг от друга. В данной статье будут рассмотрены самые популярные показатели, и для опытных читателей сразу оглавление:

и, чтобы не «лепить» километровую простыню, разделю материал на две веб страницы:

Итак, прямо сейчас мы сформулируем определения этих показателей, узнаем соответствующие формулы и, конечно, потренируемся в конкретных вычислениях. Да не просто в конкретных, а в рациональных.

Но прежде систематизируем информацию о том, какие статистические данные могут оказаться в нашем распоряжении:

– они могут быть первичными (не обработанными), грубо говоря – это неупорядоченный список чисел, либо вторичными – это уже сформированный дискретный (Урок 2) или интервальный вариационный ряд (Урок 3).

– рассматриваемая статистическая совокупность может быть генеральной либо выборочной, и чаще, конечно, перед нами выборка.

…что-то не понятно по терминам? Срочно изучать основы предмета (Урок 1)! – это быстро и интересно, ну а я, сколько нужно, вас тут подожду 🙂

Размах вариации

Он уже встречался. Это разность между самым большим и самым малым значением статической совокупности:

при этом не имеет значения, генеральная ли нам дана совокупность или выборочная, сгруппированы ли данные или нет.

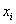
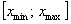
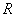
Очевидно, что все варианты исследуемой совокупности (той или иной) заключены в отрезке , а размах – есть не что иное, как его длина.

Такой вот простой, надёжный и понятный показатель. Но, несмотря на его элементарность, рассмотрим технику вычисления, и, конечно, это отличный повод размяться:

Дана статистическая совокупность
15, 17, 13, 10, 21, 17, 23, 9, 14, 19

Найти размах вариации

Решить задачу можно несколькими способами.

Способ первый, суровый – продолжаю вас готовить к борьбе с киборгами :)) Это когда под рукой нет вычислительной техники. Или когда она есть, но вы сами понимаете, как важно «прокачать» свои человеческие способности.

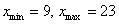
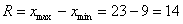
Если чисел не так много (наш случай), то максимальное и минимальное значения легко углядеть устно: и размах равен: единиц.

Если чисел больше (20-30 и даже больше), то надёжен следующий алгоритм:

1) Ищем минимальное значение. Сначала самым маленьким будет первое число: 15. Второе число (17) больше, и поэтому его пропускаем. Третье число (13) меньше, чем 15, и теперь 13 – самое малое число. И так далее, пока не закончится список.

2) Ищем максимальное значение. Сначала самым большим будет первое число: 15. Второе число (17) больше и теперь оно становится самым большим. И так далее – до конца списка.

Способ второй, более быстрый (обычно). Использование программного обеспечения, при этом числа можно просто отсортировать (по возрастанию либо убыванию) или использовать специальные функции:

Запишем ответ 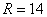ед. и с нетерпением перейдём к другим показателям, которые характеризуют степень рассеяния вариант относительно центра совокупности, прежде всего, относительно средней.

О смысле и важности этих показателей я рассказал в курсе теории вероятностей (статья о дисперсии дискретной случайной величины), но коротко повторю и сейчас. Рассмотрим двух студентов, каждый из которых в среднем учится на 3,5 балла. Но есть один нюанс. Один стабильно получает тройки-четвёрки, а другой то пятёрки, то двойки. И поэтому важно знать меру рассеяния оценок относительно средней величины. Чем она меньше – тем стабильнее учится студент.

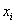
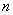
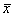
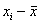
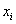
Эту меру можно оценить следующим образом: из каждой оценки (пусть их будет штук) вычитаем среднее значение . Величина называется отклонением (значения ) от средней.

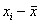
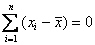
Теперь эти отклонения нужно просуммировать, но тут появляется проблема: среди разностей есть как положительные, так и отрицательные, и при их суммировании будет происходить взаимоуничтожение отклонений. Более того, итоговая сумма равна нулю: , и мы не получаем желаемого результата.

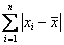
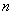
Вопрос можно решить с помощью модуля, который уничтожает минусы: , после чего осталось разделить сумму на объём совокупности и получить:

среднее линейное отклонение

– есть среднее арифметическое абсолютных отклонений всех значений статистической совокупности от средней. Это формула для несгруппированных статистических данных.

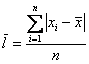
Если же в нашем распоряжении есть сформированный дискретный либо интервальный вариационный ряд, то формула будет такой:

, где – варианты (для дискретного ряда) либо середины частичных интервалов (для интервального ряда), а – соответствующие частоты.

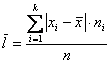
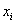
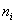
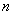
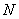
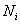
Напоминаю, что маленькая буква обычно используется для выборочной совокупности, а большая – для генеральной: – объём ген. совокупности, – частоты.

И начнём мы с малого:

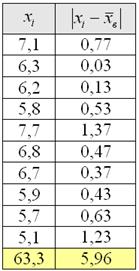
В результате 10 независимых измерений некоторой величины, выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице

Требуется вычислить среднее линейное отклонение

Решение: очевидно, что перед нами первичные данные и выборочная совокупность (теоретически измерений можно провести бесконечно много). На первом шаге вычислим выборочную среднюю:

Теперь находим модули отклонений от средней: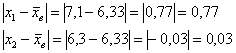

…
и так далее до:

Вычисления удобно проводить на калькуляторе или в Экселе, а результаты заносить в таблицу:

На завершающем этапе рассчитываем сумму модулей:
и среднее линейное отклонение:
ед. – оно означает, что измеренные значения в среднем отличаются от примерно на 0,6 ед.

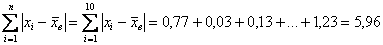
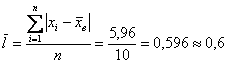
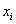
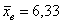
Но помимо этого, для оценки рассеяния вариант относительно средней существует более совершенный и распространённый подход. Он состоит в том, чтобы использовать не модули, а возведение отклонений в квадрат: 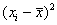(чтобы ликвидировать встречающиеся отрицательные значения).

Генеральная и выборочная дисперсия

Дисперсия с латыни так и переводится – рассеяние.

…не сломать бы язык 🙂 …так… Выборочная дисперсия – это среднее арифметическое квадратов отклонений всех вариант выборки от её средней:
– для несгруппированных данных, и:

– для сформированного вариационного ряда, где – кратные (одинаковые по значению) варианты в дискретном случае либо середины частичных интервалов – в интервальном, и – соответствующие частоты.

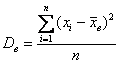
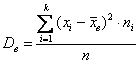
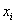
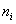
Еще раз не спеша и ОСМЫСЛЕННО прочитайте определение и выполните

Сформулировать и записать (на бумагу!) определение генеральной дисперсии и соответствующие формулы.

Свериться можно, как обычно, в конце урока.

После чего следует

продолжение Примера 13

По тем же исходным данным вычислить выборочную дисперсию

Без проблем. Вместо модулей рассчитываем квадраты отклонений:

заполняем табличку: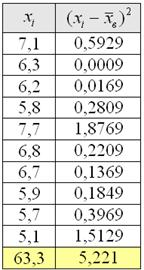

и порядок:
квадратных (!) единиц – коль скоро, мы возводили в квадрат. И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь корень. Но мы не будем торопить события, лучше посмотрим, как выполнять вычисления в Экселе:

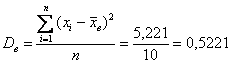
Ответ:

Разобранная задача де-факто встречается в лабораторных работах по физике (да и не только) – когда некоторая величина замеряется раз 10 и затем рассчитывается среднее значение.

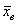
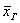
А теперь представьте, что вся ваша группа выполняет лабу по физике, и каждый провёл по 10 испытаний в схожих условиях. Очевидно, что у всех получились несколько разные выборочные значения , но все они без какой-либо закономерности (в общем случае) будут варьироваться вокруг истинного значения показателя (роль генеральной средней может играть некий теоретический эталон). Это свойство (отсутствие закономерности) называется несмещённостью оценки генеральной средней, и справедливо оно, как мы увидим ниже, не для всех показателей.

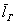
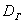
Теперь пару ласковых об отклонениях. В чём их смысл? Всё просто: у кого эти показатели ниже, тот качественнее проводит опыты (плавнее выполняет действия, точнее снимает показания с приборов, засекает время и т.п.). В идеале эти отклонения равны нулю, но это только в идеале – сам эмпиризм ситуации порождает генеральное линейное отклонение и генеральную дисперсию, которые обусловлены человеческим фактором, погрешностью приборов и так далее – вплоть до магнитных бурь.

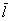
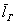
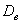
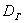
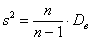
В случае с полученными линейными отклонениями – всё то же самое, они будут безо всякой закономерности варьироваться вокруг генерального значения . Но вот с дисперсией всё не так. Полученные значения выборочной дисперсии будут давать систематически заниженную оценку генеральной дисперсии . И поэтому выборочную дисперсию следует «поправить» по формуле:

– желающие могут найти обоснование этого факта и этой формулы в специализированной литературе по математической статистике.

Показатель 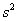так и называется – исправленная выборочная дисперсия, и вот она уже является несмещённой оценкой генеральной дисперсии.

Таким образом, каждый студент должен поправить свою дисперсию, в частности, для Примера 13:

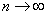
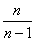
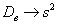
Следует отметить, что для большой выборки (от 100 и даже от 30 вариант) этой поправкой можно пренебречь, так как при дробь стремится к единице и .

И иногда дисперсию можно вовсе не поправлять. Так, в разобранном примере от нас требовалось просто вычислить выборочную дисперсию и всё. А если хочется что-то додумать, то пусть этого захочет преподаватель 🙂 Но вот если дисперсия будет «участвовать» в дальнейших действиях, то, конечно, приводим её к виду .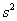

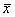
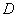
Более того, встречаются задачи, где вообще не понятно – выборочная ли дана совокупность или генеральная, и тогда разумно проявить аккуратность и использовать обозначения без подстрочных индексов, в частности, и .

Теперь случай, когда дан готовый вариационный ряд. У меня опять есть подходящая советская задача про телефонную станцию, но я скорректирую условие в соответствии с современными реалиями:

В результате выборочного исследования звонков, статистик МТС получил следующие данные (за некоторый временной промежуток):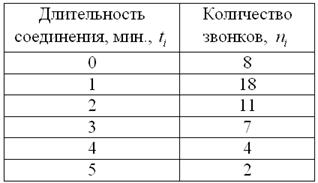

…у ОпСоСов, как известно, своя статистика – с округлением до ближайшей целой минуты :), впрочем, это тоже устареет…, как метко заметил современник, дети дружно играли во дворе – каждый в своём смартфоне(

Найти размах вариации, среднее линейное отклонение и выборочную дисперсию. Дать несмещённую оценку генеральной дисперсии и пояснить, что это означает.

Решить данную задачу в Экселе (данные и гайд уже там) либо на бумаге с помощью калькулятора.

Краткое решение и ответ совсем близко, поскольку 1-я часть урока подошла к концу, и я жду вас во 2-й части, где мы рассмотрим формулу для вычисления дисперсии, среднее квадратическое отклонение и коэффициент вариации.

Задание. Генеральная дисперсия – это среднее арифметическое квадратов отклонений всех вариант генеральной совокупности от её средней: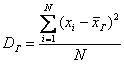
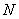
, где – объём генеральной совокупности.
Для сформированного вариационного ряда формула принимает вид: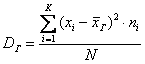
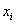
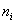
, где – либо варианты дискретного ряда, либо середины частичных интервалов интервального ряда, а – соответствующие частоты.

Пример 14. Решение: найдём размах вариации: 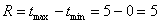мин.

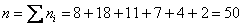
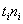
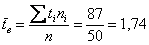
Вычислим объём совокупности , произведения , их сумму и выборочную среднюю мин.
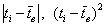
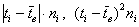
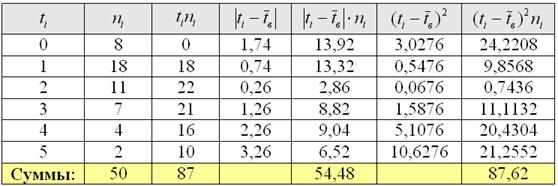
Рассчитаем , произведения и их суммы:

Среднее линейное отклонение:
мин.
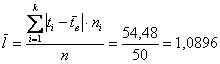
Выборочная дисперсия:
мин. в квадрате.
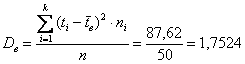
Несмещённой оценкой генеральной дисперсии является исправленная выборочная дисперсия:
мин. в квадрате.
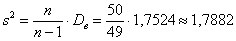
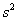
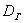
Несмещённость означает, что если в схожих условиях проводить аналогичные выборки, то полученные значения будут безо всякой закономерности варьироваться вокруг генерального значения .

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник