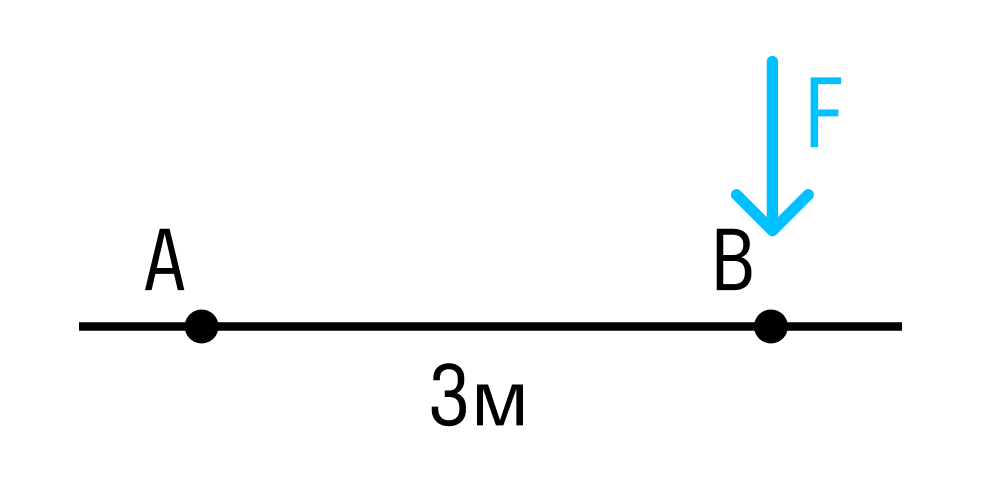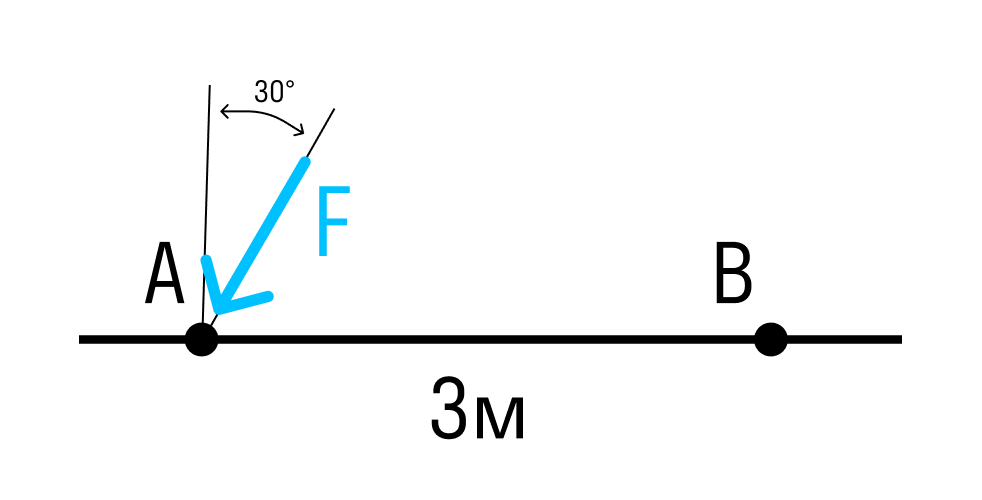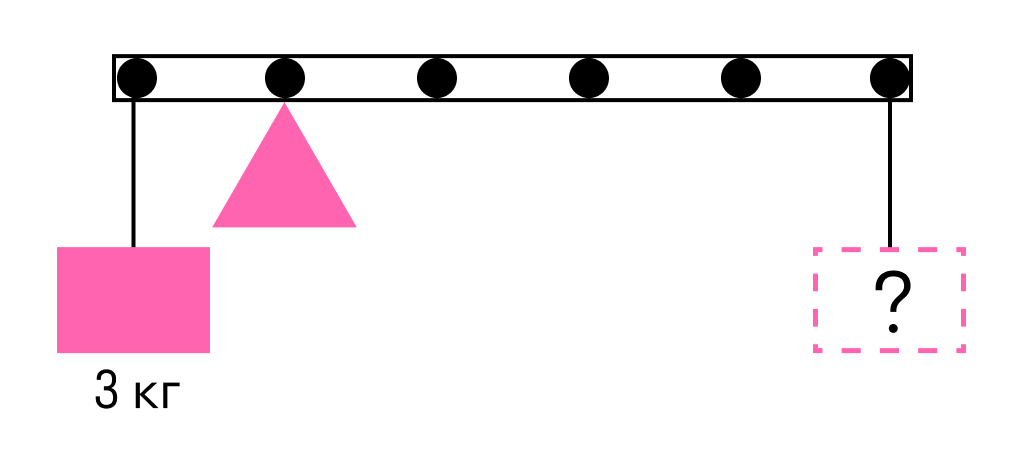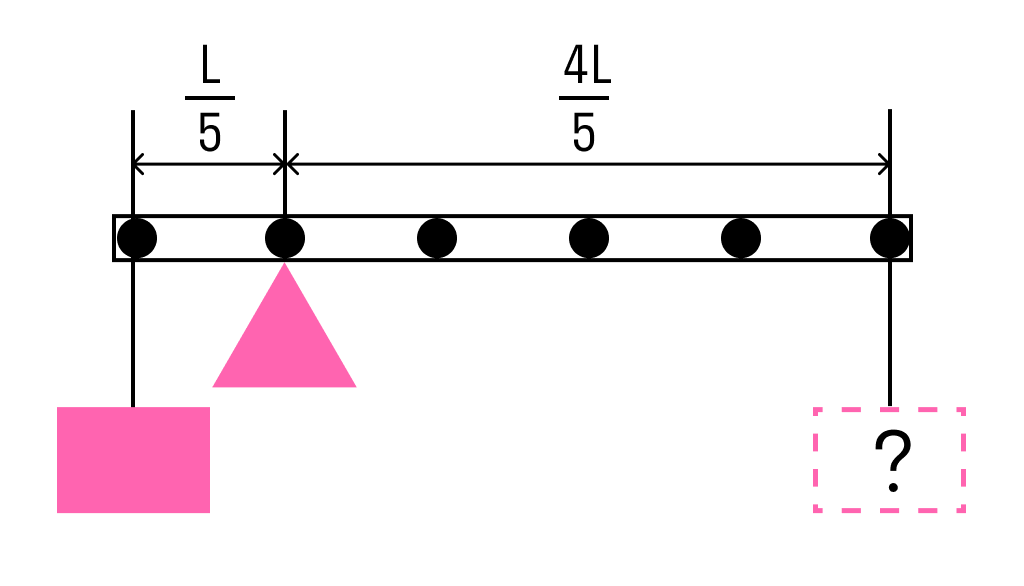Что называется вращающим моментом в каких единицах он измеряется
Момент силы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
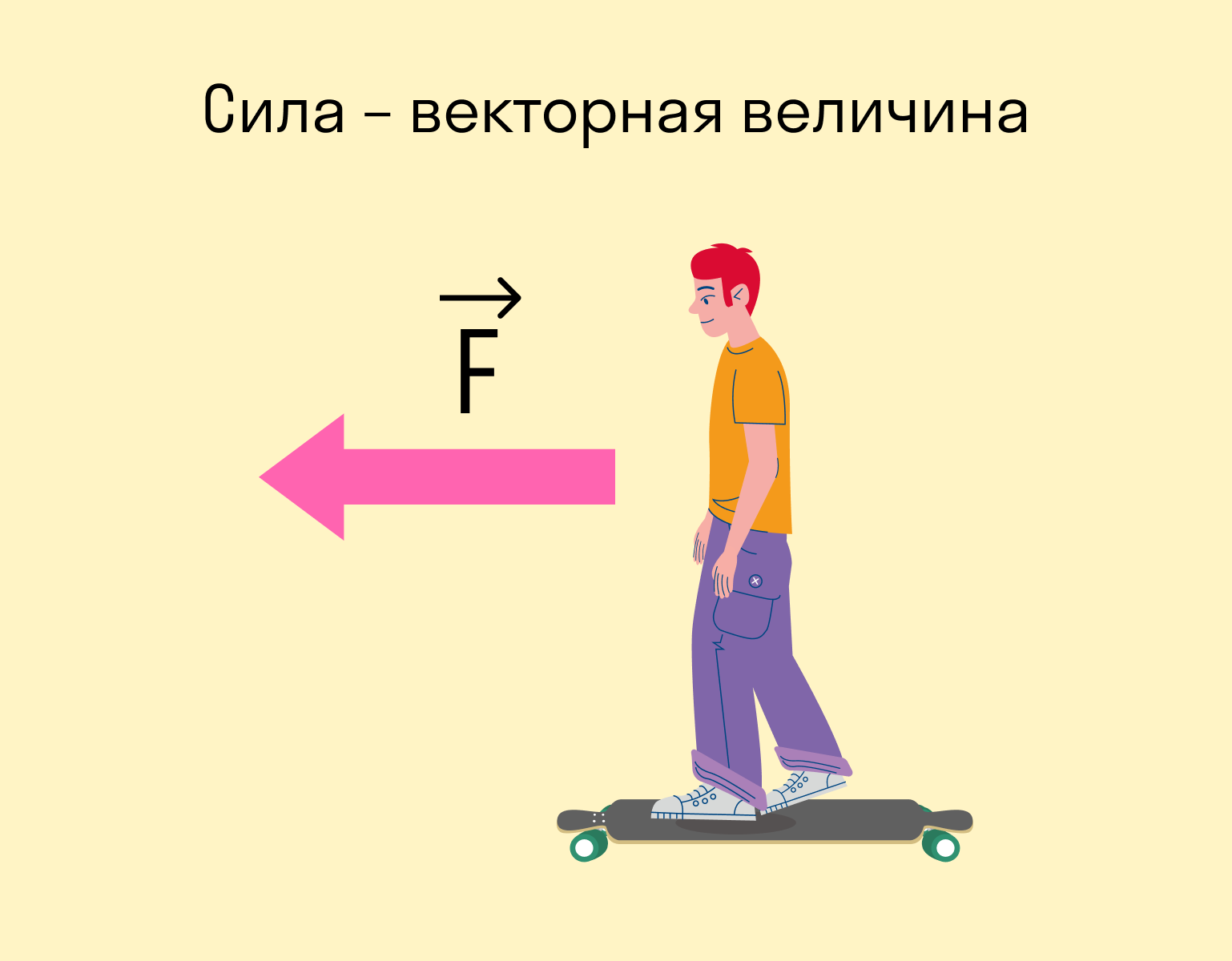
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.
Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.
На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.
То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
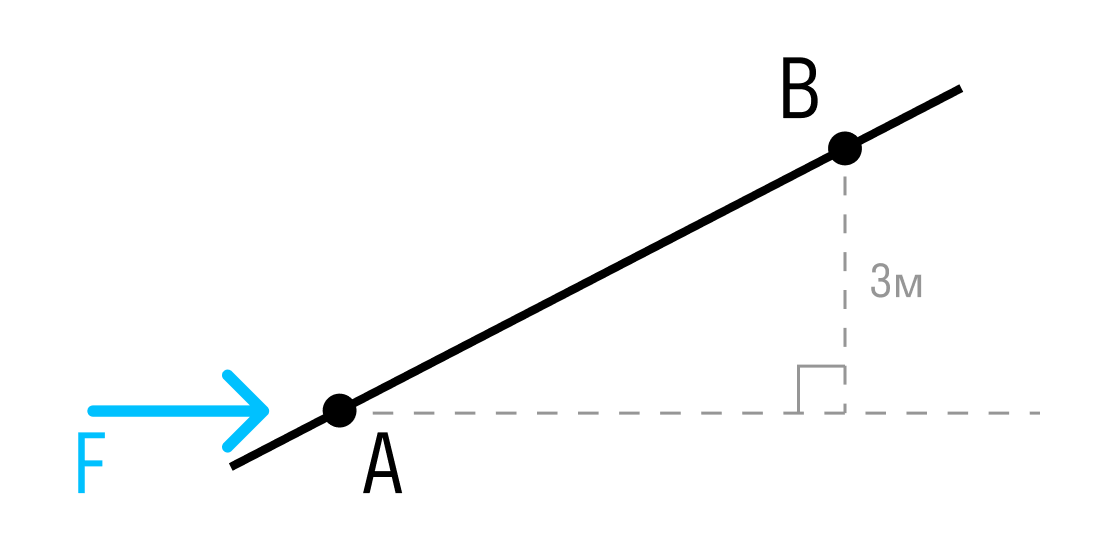
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn = M’1 + M’2 +. + M’n
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
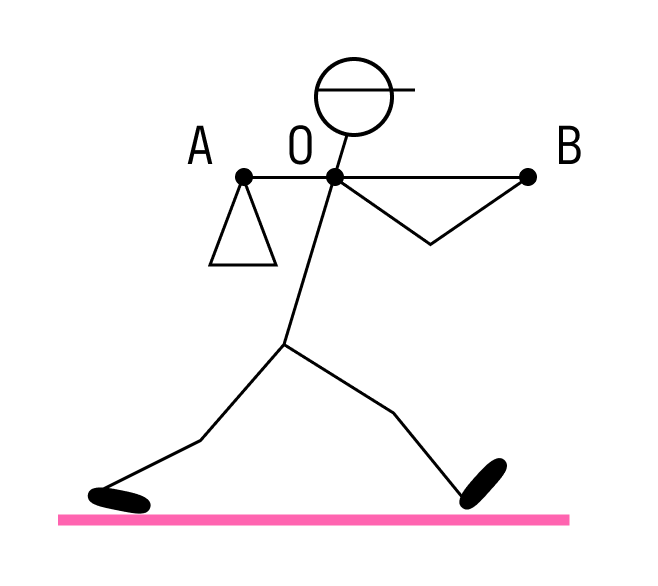
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
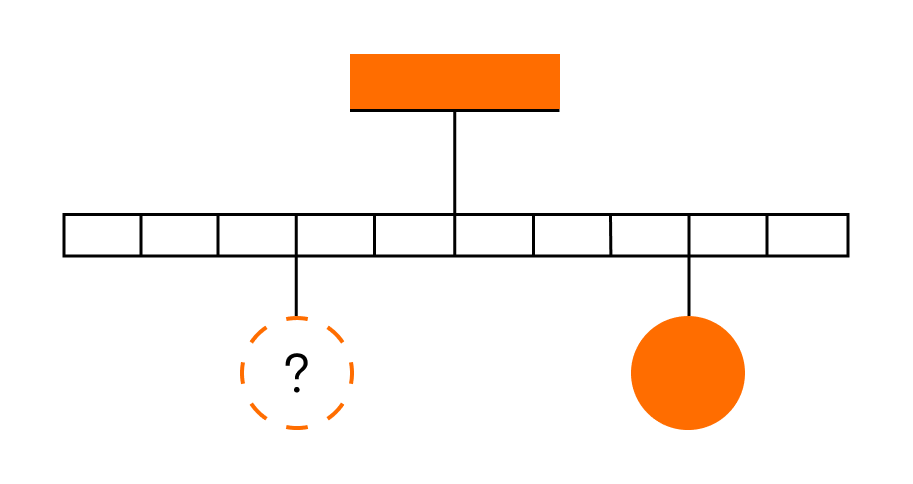
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага m1g*l1=m2g*l2
Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг
Ответ: Масса груза равна 0,3 кг
Задача 4
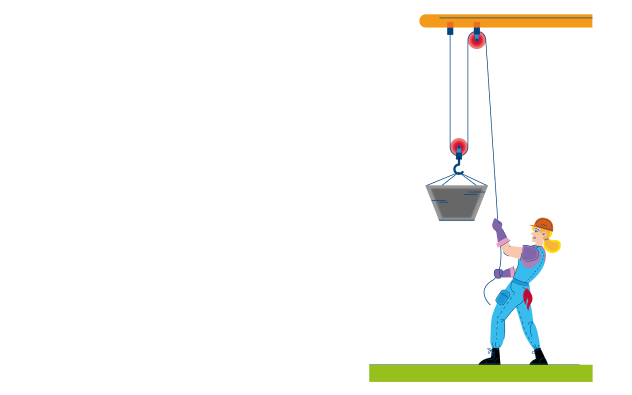
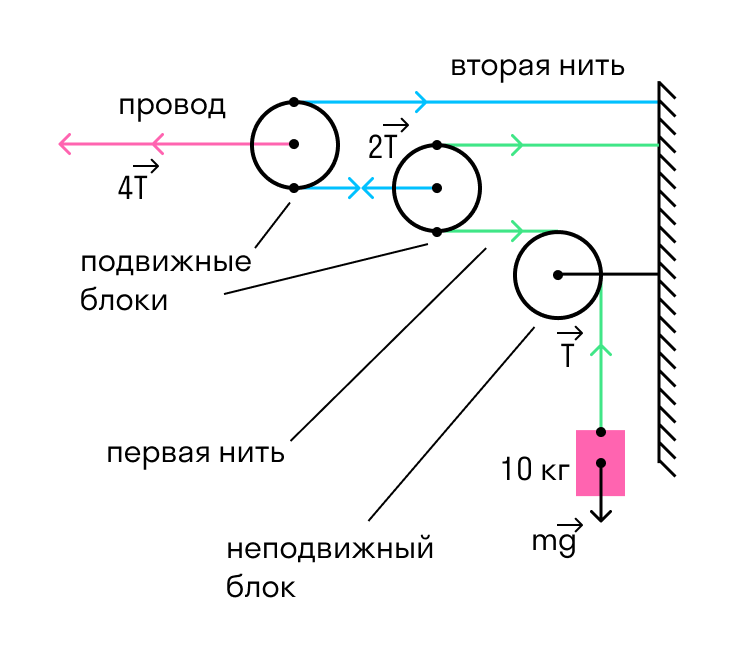
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?
Решение:
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н
Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно
Ответ: натяжение провода равно 400 Н
Задача 5 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
ВРАЩАЮЩИЙ МОМЕНТ
Смотреть что такое ВРАЩАЮЩИЙ МОМЕНТ в других словарях:
ВРАЩАЮЩИЙ МОМЕНТ
мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. В. м. равен алгебраической сумме моментов всех действующих на вращаю. смотреть
ВРАЩАЮЩИЙ МОМЕНТ
ВРАЩАЮЩИЙ МОМЕНТ, мера внеш. воздействия, изменяющего угловую скорость вращающегося тела. В. м. равен алгебраич. сумме моментов всех действующих на в. смотреть
ВРАЩАЮЩИЙ МОМЕНТ
ВРАЩАЮЩИЙ МОМЕНТ, вращающее действие силы. Так, турбина при повороте генератора создает вращающий момент по оси вращения. Мощность ротационного двигате. смотреть
ВРАЩАЮЩИЙ МОМЕНТ
мера внеш. воздействия, изменяющего угловую скорость вращающегося тела. В. м. Мвр равен сумме моментов всех действующих на тело сил относительно оси вр. смотреть
ВРАЩАЮЩИЙ МОМЕНТ
ВРАЩАЮЩИЙ МОМЕНТ
ВРАЩАЮЩИЙ МОМЕНТ
ВРАЩАЮЩИЙ МОМЕНТ
ВРАЩАЮЩИЙ МОМЕНТ
ВРАЩАЮЩИЙ МОМЕНТ
momento di rotazione
ВРАЩАЮЩИЙ МОМЕНТ
мера внеш. силового воздействия на вращающееся тело, изменяющего угловую скорость вращения (см. Момент силы).
ВРАЩАЮЩИЙ МОМЕНТ
1) driving torque 2) running torque 3) turning moment
ВРАЩАЮЩИЙ МОМЕНТ
turning moment, driving torque, running torque, torque* * *torque
ВРАЩАЮЩИЙ МОМЕНТ
torque moment, torsional moment, rotational moment, turning moment, torque, turning couple
ВРАЩАЮЩИЙ МОМЕНТ
drehendes Moment, Triebmoment
ВРАЩАЮЩИЙ МОМЕНТ
moment [couple] de rotation
ВРАЩАЮЩИЙ МОМЕНТ
rotative moment, turning moment, axial torque, torque
Крутящий момент двигателя: что это такое
Крутящий момент мотора (он же вращательный момент, или момент силы) – это векторная физическая величина, характеризующая вращательное действие силы на твёрдое тело и равная векторному произведению радиус-вектора, который проведёт от оси вращения к точке приложения силы. В физике момент силы понимается в качестве «вращающей силы». В общепринятой системе единиц единицей измерения момента силы стал Ньютон-метр (Н.м). 1 Н.м равен силе в 1 Ньютон, приложенной к рычагу в 1 метр.
Крутящий момент и лошадиная сила
Автолюбители нередко дискутируют друг с другом: чей двигатель мощнее. Но иногда и не представляют при этом, из чего складывается данный параметр. Общепринятый термин «лошадиная сила» был введён изобретателем Джеймсом Уаттом в XVIII веке. Он придумал его, наблюдая за лошадью, которая была запряжена в поднимающий уголь из шахты механизм. Он рассчитал, что одна лошадь за минуту может поднять 150 кг угля на высоту 30-ти метров. Одна лошадиная сила эквивалентна 735,5 Ватт, или 1 кВт равен 1,36 л.с.
В первую очередь, мощность любого мотора оценивают в лошадиных силах, и лишь потом вспоминают о крутящем моменте. Но эта тяговая характеристика тоже даёт представление о конкретных тягово-динамических возможностях автомобиля. Крутящий момент является показателем работы силового агрегата, а мощность – основным параметром выполнения этой работы. Эти показатели тесно связаны друг с другом. Чем больше производится двигателем лошадиных сил, тем больше и потенциал крутящего момента. Реализуется этот потенциал в реальных условиях через трансмиссию и полуоси машины. Соединение этих элементов вместе и определяет, как именно мощность может переходить в крутящий момент.
Простейший пример – сравнение трактора с гоночной машиной. У гоночного болида лошадиных сил много, но крутящий момент требуется для увеличения скорости через редуктор. Чтобы такая машина двигалась вперёд, надо совсем немного работы, потому что основная часть мощности используется для развития скорости.
Что касается трактора, то у него может быть мотор с таким же рабочим объёмом, который вырабатывает столько же лошадиных сил. Но мощность в этом случае используется не для развития скорости, а для выработки тяги (См. тяговый класс). Для этого она пропускается через многоступенчатую трансмиссию. Поэтому трактор не развивает высоких скоростей, зато он может буксировать большие грузы, пахать и культивировать землю, и т.д.
В двигателях внутреннего сгорания сила передаётся от газов сгорающего топлива поршню, от поршня – передаётся на кривошипный механизм, и далее на коленчатый вал. А коленвал, через трансмиссию и приводы, раскручивает колёса.
Естественно, крутящий момент двигателя не постоянен. Он сильней, когда на плечо действует бо́льшая сила, и слабей – когда сила слабнет или перестаёт действовать. То есть, когда водитель давит на педаль газа, то сила, воздействующая на плечо, повышается, и, соответственно увеличивается крутящий момент двигателя.
Мощность обеспечивает преодоление всевозможных сил, которые мешают двигаться автомобилю. Это и сила трения в двигателе, трансмиссии и в приводах автомобиля, и аэродинамические силы, и силы качения колёс и т.д. Чем больше мощность, тем большее сопротивление сил машина сможет преодолеть и развить большую скорость. Однако мощность – сила не постоянная, а зависящая от оборотов мотора. На холостом ходу мощность одна, а на максимальных оборотах – совершенно другая. Многими автопроизводителями указывается, при каких оборотах достигается максимально возможная мощность автомобиля.
Зачастую водитель сталкивается с такими ситуациями, когда требуется придать автомобилю значительное ускорение для выполнения необходимого маневра. Прижимая педаль акселератора в пол, он чувствует, что автомобиль ускоряется слабо. Для быстрого ускорения нужен мощный крутящий момент. Именно он и характеризует приёмистость автомобиля.
Основную силу в двигателе внутреннего сгорания вырабатывает камера сгорания, в которой воспламеняется топливно-воздушная смесь. Она приводит в действие кривошипно-шатунный механизм, а через него – коленчатый вал. Рычагом является длина кривошипа, то есть, если длина будет больше, то и крутящий момент тоже увеличится.
Однако увеличивать кривошипный рычаг до бесконечности невозможно. Ведь тогда придётся увеличивать рабочий ход поршня, а вместе с ним и размеры двигателя. При этом уменьшатся и обороты двигателя. Двигатели с большим рычагом кривошипного механизма можно применить только лишь в крупномерных плавательных средствах. А в легковых автомашинах с небольшими размерами коленчатого вала не поэкспериментируешь.
Физические определения мощности и крутящего момента двигателя
Из курса физики за девятый класс нам известно, что крутящий момент М равняется произведению силы F, прикладываемой к рычагу длиной плеча L. Высчитывается он по формуле: М = F * L.
Определение мощности мотора и понимание данного параметра, сложившееся в науке, звучит следующим образом: это физическая величина, которая характеризует работу двигателя, выполняемую им за определённое время. То есть, мощность показывает, как быстро машина, имеющая определённую массу, сможет преодолеть определённое расстояние. Чем выше мощность, тем большую максимальную скорость разовьёт автомобиль при его неизменной снаряжённой массе. В классической физике мощность измеряют в ваттах или киловаттах, а лошадиная сила является внесистемной единицей измерения.
Понимание крутящего момента сложнее. Крутящим моментом двигателя является качественный показатель, который характеризует силу вращения коленчатого вала мотора. Рассчитывается он как произведение силы, приложенной к поршню, на плечо (т.е. расстояние от центра оси вращения коленвала до места крепления поршня (шатунной шейки). Крутящий момент напрямую зависит от силы давления газов в цилиндре на поршень, а также от рабочего объёма мотора и от степени сжатия топливно-воздушной смеси в цилиндрах. Значительно более высоким крутящий момент получается у дизельных двигателей – как раз потому, что у них чрезвычайно высока степенью сжатия смеси солярки и воздуха в камерах сгорания.
Высокий крутящий момент двигателя даёт автомашине лучшую динамику разгона, уже при низких оборотах вращения коленчатого вала, существенным образом увеличивает тяговые характеристики мотора: повышает грузоподъёмность машины и её проходимость.
Своего наибольшего значения крутящий достигает при определённых оборотах. Моторам бензиновым оборотов требуется больше, чем дизелям. По сути, мощность двигателя является вторичной рабочей характеристикой мотора, которая является производной крутящего момента. Она линейно зависима от частоты вращения коленвала: чем обороты выше, тем больше и мощность мотора (естественно, до определённых пределов).
Крутящий момент тоже увеличивается при увеличении оборотов двигателя. Но, достигнув своего наивысшего значения (при определённой частоте вращения коленчатого вала), его показатели начинают понижаться, уже вне зависимости от дальнейшего прироста оборотов.
Как изменение крутящего момента влияет на динамику машины
Чтобы обеспечить как можно более высокие динамические характеристики машины, автопроизводителями разрабатываются такие силовые агрегаты, которые обладают максимальным крутящим моментом в более широком диапазоне оборотов мотора. Высокий крутящий момент характерен для дизелей, а также для моторов многоцилиндровых и турбированных.
Чтобы реально оценить роль мощности и крутящего момента при формировании динамических характеристик машины, требуется учесть следующее:
Таким образом, вне зависимости от мощности двигателя, разгонная динамика машины, его способность без проблем преодолевать подъёмы всецело зависят от того, каков максимальный крутящий момент. Чем больший крутящий момент передастся на ведущие колёса, и чем шире диапазон оборотов мотора, в котором он будет достигнут, тем увереннее автомобиль будет ускоряться и преодолевать непростые участки дорог.
Необходимо заметить, что прямое сравнение характеристик конструкционно идентичных, но имеющих различные крутящие моменты двигателей, будет иметь смысл только при одинаковых параметрах и трансмиссии тоже – когда коробки переключения передач будут обладать схожими передаточными отношениями. Если же эти параметры будут разными, то и сравнивать крутящие моменты и возможности двигателей нет практического смысла.
Крутящий момент у бензиновых и дизельных моторов
Бензиновые двигатели отличаются не самым большим крутящим моментом. Своего наибольшего значения крутящий момент бензинового двигателя достигает на оборотах не менее чем 3-4 тыс. об/мин. Однако бензиновый двигатель быстро сможет увеличить мощность и раскрутиться до 7-8 тыс. об/мин. При таких сверхвысоких оборотах мощность возрастает в разы.
Дизельный двигатель не отличается высокими оборотами. Обычно это 3-5 тыс. об/мин максимум, и тут он бензиновым моторам проигрывает. Однако крутящий момент дизельного двигателя выше в разы, и доступным он становится очень быстро, практически с холостого хода.
В качестве конкретного примера, можно вспомнить тесты двух двигателей от фирмы Ауди – один дизельный: 2.0 TDI мощностью 140 л.с. и крутящим моментом 320 Н.м, а второй бензиновый: 2.0 FSI мощностью 150 л.с. и крутящим моментом 200 Н.м. По итогам контрольной прогонки в различных режимах получается, что дизель на целых 30-40 л.с. мощнее бензинового двигателя в диапазоне от 1 до 4,5 тыс. оборотов. Поэтому и не сто́ит смотреть только на лошадиные силы. Бывает, что мотор с меньшим рабочим объёмом, но с высоким крутящим моментом показывает себя намного динамичнее, чем двигатель с большим рабочим объёмом, но низким крутящим моментом.
В технических характеристиках, которые указываются для каждого автомобиля и его двигателя, показатель максимального крутящего момента всегда указывается в сочетании с величиной оборотов, при которых такой крутящий момент может быть достигнут. При этом обычно считается: если максимальный крутящий момент может быть достигнут на оборотах до 4,5 тыс. об/мин., то такой двигатель можно назвать низкооборотным; а если более 4,5 тыс. об/мин – то высокооборотным.
При малом количестве оборотов в область сгорания поступает незначительное количество воздушно-топливной смеси за единицу времени, поэтому крутящий момент и мощность невелики. Увеличивая обороты, количество топливно-воздушной смеси (а вслед за ним и мощность, и крутящий момент) возрастают. Достигая значительных параметров, мощность начинает снижаться из-за механических потерь на трение механизмов; инерционных потерь; от недостаточного нагнетания воздуха (именуемого кислородным голоданием).
Из соображений обеспечения максимальных количеств поступающего воздуха в камеру сгорания даже на незначительных оборотах двигателя применяются системы турбированного наддува с электронным регулированием. Применяя такие системы турбонаддува, можно обеспечивать равномерность характеристик крутящего момента в широком диапазоне оборотов двигателя.
Какие можно сделать выводы по вышесказанному
Оценивая эксплуатационные параметры автомобиля и непосредственно рабочие характеристики его мотора, величина крутящего момента будет обладать большим приоритетом, чем мощность. Среди двигателей, которые имеют примерно одинаковые конструктивные и рабочие параметры, более предпочтительными будут те, у которых крутящий момент выше.
Для обеспечения лучшей динамики разгона машины и обеспечения оптимальных тяговых свойств двигателя, частоту вращения коленчатого вала надо поддерживать в том диапазоне значений, при которых крутящий момент может достичь пиковых своих показателей.
В итоге, можно сделать вывод о том, что классифицировать и сравнивать машины только по мощности (лошадиных силам) двигателя не совсем правильно. Необходимо обращать особенное внимание ещё и на крутящий момент (Н.м). Если крутящий момент двигателя значительно выше, чем у аналогичного или близкого по ТТХ конкурента, то такой мотор будет обладать бо́льшей динамикой.
Для движения в городском ритме лучше всего подходят низкооборотные моторы с турбонаддувом. Если же есть желание посоперничать в скоростях на трассе, то лучше выбрать автомобиль с высокооборотным силовым агрегатом.
Способы прироста в крутящем моменте двигателя
Величину, которая необходима для крутящего момента той или иной модели автомобиля, определяют инженеры ещё на предварительном этапе конструкторской разработки мотора. От неё зависят и другие элементы автомобиля: его подвеска, тормозное и рулевое управление, аэродинамика. Поэтому, прежде чем приступать к самостоятельному форсированию двигателя, важно убедиться, что машина не развалится от умощнения двигателя.
Способов увеличения крутящего момента и, вместе с ним, мощности двигателя, может быть много:
Однако принудительное увеличение крутящего момента и мощности двигателя в значительной степени уменьшает ресурс его работы.
Как правильно разгоняться, используя максимальный крутящий момент
Для этого важно уметь работать с коробкой передач. Для максимального разгона надо переключаться так, чтобы обороты упали примерно на пик крутящего момента либо выше него, но чтобы оставался запас по увеличению оборотов – разгон больше оборотов максимальной мощности будет проходить медленней. Идеальным вариантом на обычных машинах можно назвать разгон «от пика момента до пика мощности». В тоже время, на двигателях современных автомобилей электроника просто не даст «перекрутить» мотор более его пика мощности – произойдёт «отсечка».