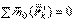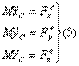Что называется внешними и внутренними силами
изучаем сопротивление материалов
Внешние и внутренние силы
Внешние силы
Внешняя сила — это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. К внешним силам относятся также реакции опор (связей).
Все внешние нагрузки можно разделить на статические и динамические.
Статическими считаются нагрузки, в процессе приложения которых возникающие силы инерции малы и ими можно пренебречь.
Если силы инерции велики (к примеру – землетрясение) – нагрузки считаются динамическими. Примерами таких нагрузок также могут служить внезапно приложенные нагрузки, ударные и повторно-переменные.
Внезапно приложенные нагрузки передаются на сооружение сразу
полной своей величиной (к примеру давление колес локомотива, входящего на мост).
Ударные нагрузки возникают при быстром изменении скорости соприкасающихся элементов конструкции, например» при ударе бабы копра о сваю при ее забивке.
Повторно-переменные нагрузки действуют на элементы конструкции, повторяясь значительное число раз. Таковы, например, повторные давления пара, попеременно растягивающие и сжимающие шток поршня и шатун паровой машины. Во многих случаях нагрузка представляет собой комбинацию нескольких видов динамических воздействий.
Внутренние силы
В результате действия внешних сил в теле возникают внутренние силы.
Внутренняя сила — силы взаимодействия между частями одного тела, возникающие под действием внешних сил.
Внутренние силы являются самоуравновешенными, поэтому они не видны и не влияют на равновесие тела. Определяют внутренние силы методом сечения.
Внешние нагрузки приводят к следующим видам напряженно-деформированного состояния:
Механическая система. Силы внешние и внутренние
Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин».
Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.
Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.
Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.
Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.
В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.
Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.
Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.
Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.
Активными или задаваемыми силами называются все остальные силы, все кроме реакций.
Необходимость этой классификации сил выяснится в следующих главах.
Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.
Внутренние силы обладают следующими свойствами:
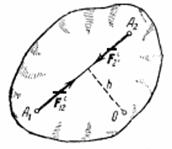
1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.31) действуют друг на друга с равными по модулю и противоположно направленными силами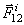 
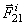
и 
, сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то
Внешние и внутренние силы действующие на материальную точку
Силы, действующие на любую точку механической системы, делятся на внутренние и внешние.
Fi – внутренняя сила
Fe – внешняя сила
Внутренними называются силы, с которыми точки, входящие в систему, действуют друг на друга.
Внешними называются силы, которые прикладываются к точкам извне, то есть от других точек или тел, не входящих в систему. Разделение сил на внутренние и внешние условное.
Fтр – внутренняя сила
Механическая система. Силы внешние и внутренние.
Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.
Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.
Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.
Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.
В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.
Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.
Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.
Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.
Активными или задаваемыми силами называются все остальные силы, все кроме реакций.
Необходимость этой классификации сил выяснится в следующих главах.
Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.
Внутренние силы обладают следующими свойствами:
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. Действительно, если взять произвольный центр О, то из рис.18 видно, что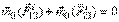 
. Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет: 
Из доказанных свойств не следует однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызывать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твердое тело.
30Теорема о движении центра масс.
Теорема о движении центра масс механической системы: центр масс механической системы движется как материальная точка, масса которой равняется массе системы, и к которой приложены все внешние силы, действующие на систему
Выводы:
Механическую систему или твердое тело можно рассматривать как материальную точку в зависимости от характера ее движения, а не от ее размеров.
Внутренние силы не учитываются теоремой о движении центра масс.
Теорема о движении центра масс не характеризует вращательное движение механической системы, а только поступательное
Закон о сохранении движения центра масс системы:
1. Если сумма внешних сил (главный вектор) постоянно равен нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
2. Если сумма проекций всех внешних сил на какую-нибудь ось равняется нулю, то проекция скорости центра масс системы на эту же ось величина постоянная.
Уравнение и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. Сравнивая с уравнением движения материальной точки, получаем другое выражение теоремы: центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.
(4’) – выражает теорему о движении центра масс системы: центр масс системы движется как материальная точка, на которую действуют все силы системы.
Выводы:
1. Внутренние силы не оказывают влияния на движение центра масс системы.
2. Если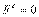 
, движение центра масс системы происходит с постоянной скоростью.
3. 
, то движение центра масс системы в проекции на ось происходит с постоянной скоростью.
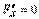
Эти уравнения представляют собою дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.
Значение доказанной теоремы состоит в следующем.
1) Теорема дает обоснование методам динамики точки. Из уравнений видно, что решения, которые мы получаем, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела, т.е. имеют вполне конкретный смысл.
В частности, если тело движется поступательно, то его движение полностью определяется движением центра масс. Таким образом, поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе тела. В остальных случаях тело можно рассматривать как материальную точку лишь тогда, когда практически для определения положения тела достаточно знать положение его центра масс.
2) Теорема позволяет при определении закона движения центра масс любой системы исключать из рассмотрения все наперед неизвестные внутренние силы. В этом состоит ее практическая ценность.
Так движение автомобиля по горизонтальной плоскости может происходить только под действием внешних сил, сил трения, действующих на колеса со стороны дороги. И торможение автомобиля тоже возможно только этими силами, а не трением между тормозными колодками и тормозным барабаном. Если дорога гладкая, то как бы не затормаживали колеса, они будут скользить и не остановят автомобиль.
Или после взрыва летящего снаряда (под действием внутренних сил) части, осколки его, разлетятся так, что центр масс их будет двигаться по прежней траектории.
Теоремой о движении центра масс механической системы следует пользоваться для решения задач механики, в которых требуется:
— по силам, приложенным к механической системе (чаще всего к твердому телу), определить закон движения центра масс;
— по заданному закону движения тел, входящих в механическую систему, найти реакции внешних связей;
— по заданному взаимному движению тел, входящих в механическую систему, определить закон движения этих тел относительно некоторой неподвижной системы отсчета.
С помощью этой теоремы можно составить одно из уравнений движения механической системы с несколькими степенями свободы.
При решении задач часто используются следствия из теоремы о движении центра масс механической системы.
Следствие 2. Если проекция главного вектора внешних сил на какую-нибудь ось равна нулю, то центр масс системы или не изменяет своего положения относительно данной оси, или движется относительно нее равномерно.
Например, если на тело начнут действовать две силы, образующие пару сил (рис.38), то центр масс С его будет двигаться по прежней траектории. А само тело будет вращаться вокруг центра масс. И неважно, где приложена пара сил.
Внешние и внутренние силы. Замкнутая система
В механике силой называют величину, характеризующую действие одного тела на другое, в результате которого происходит изменение состояния первого тела: изменяется его скорость или тело выходит из состояния покоя.
Внешние силы – это силы, действующие на тело извне. Под влиянием внешних сил тело или начинает двигаться, если оно находилось в состоянии покоя, или изменяется скорость его движения, или направление движения. Внешние силы в большинстве случаев уравновешены другими силами и их влияние незаметно, только знание законов механики позволяет утверждать о действии внешних сил на тело, находящееся в покое.
Внешние силы, действуя на твердое тело, вызывают изменения его формы, обуславливаемые перемещением частиц.
Внутренними силами являются силы, действующие между частицами, эти силы оказывают сопротивление изменению формы.
Сила — величина векторная, т. е. имеющая не только числовое значение, но и направление, поэтому действие силы на тело определяется не только ее величиной, но и ее направлением.
Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).
Внешние и внутренние силы.
Внешними называют силы, действующие на тело со стороны точек или тел, не входящих в данное тело или систему. Внутренними называют силы, с которыми точки данного тела действуют друг на друга.
Разрушение или даже просто выход из строя конструкционного элемента возможны лишь при возрастании внутренних усилий и при переходе их через некоторый предельный барьер. Высоту этого барьера удобно отсчитать от того уровня, который отвечает отсутствию внешних сил. По существу нужно принять во внимание лишь дополнительные внутренние усилия, возникающие только при наличии внешних сил. Эти дополнительные внутренние силы называют в механике просто внутренними усилиями в узком, механическом смысле.
Определяются внутренние усилия с помощью «метода сечений», в основе которого лежит достаточно очевидное утверждение: если тело в целом находится в равновесии, то и любая выделен из него часть также находится в этом состоянии
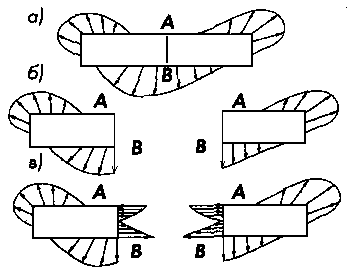
Рассмотрим стержень, находящийся в равновесии под действием системы внешних сил, рис. 2.1.5, а. Сечением АВ мысленно разделим его на две части, рис. 2.1.5, б. К каждому из сечений АВ левой и правой частей приложим систему усилий, соответствующую внутренним усилиям, действующим в реальном теле, рис. 1.7, в. Таким образом, с использованием метода сечений внутренние силы переводятся во внешние по отношению к каждой из отсеченных частей тела, что позволяет определять их из условий равновесия каждой из этих частей в отдельности.
Сечение АВ может быть ориентировало любым образом, но более удобным для дальнейших рассуждений оказывается поперечное сечение, перпендикулярное продольной оси стержня.
, 
, 
, 
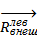
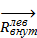
главные векторы и главные моменты внешних и внутренних сил, приложенных к левой отсеченной части. С учетом введенных обозначений условия равновесия этого тела можно записать в виде:
+ =0, 
+ =0 (2.1.1)
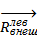
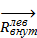
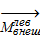
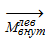
Аналогичные выражения могут быть составлены и для правой отсеченной части стержня. После несложных преобразований можно получить:
=- , =- (2.1.1)
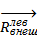
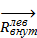
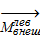
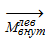
что может быть истолковано как следствие известного закона механики: действие всегда сопровождается равным и противоположно направленным противодействием.
В случае решения задачи о динамическом воздействии на стержень можно обратиться к известному принципу Даламбера, согласно которому к внешним силам присоединяются силы инерции, что вновь сводит задачу к уравнениям равновесия. Следовательно, процедура метода сечений остается
Величины 
и 
не зависят от ориентации сечения АВ (см. рис. 2.1.5). Однако в практических расчетах наиболее удобным представляется использование поперечного сечения. В этом случае нормаль к сечению совпадает с продольной осью стержня. Далее главный вектор и главный момент внутренних сил обычно представляют в виде их проекций на ортогональные оси координат, причем одна из осей (например, ось х) совмещается с упомянутой нормалью см. рис. 2.1.6.
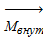
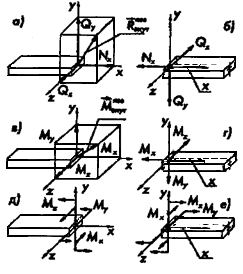
Разложим векторы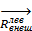 
, 
, 
, 
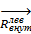
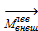
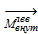
по осям координат, рис. 2.1.6, а—г. Компоненты главного вектора и главного момента имеют общепринятые названия. Усилие Nx нормальное к плоскости сечения, называют нормальной (продольной) силой, а Qx и Qy— поперечными (перерезывающими) силами. Моменты относительно осей у и z, т. e. My и Мz будут изгибающими а момент относительно продольной оси х, т.е. Мх — крутящим.
Компоненты главного момента внутренних сил в сопротивлении материалов чаще всего отображают так, как дано на рис. 2.1.6, д и е.
Векторные уравнения равновесия могут быть представлены в виде проекции на оси координат:
Таким образом, каждый компонент главного вектора для главного момента внутренних сил подсчитывается как сумма проекций всех внешних сил на соответствующую ось или как сумма моментов всех внешних сил относительно этой оси (с учетом принятого правила знаков), расположенных по одну сторону от сечения.
Дата добавления: 2016-01-18 ; просмотров: 6395 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ