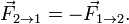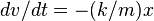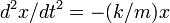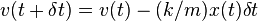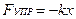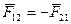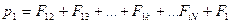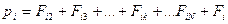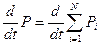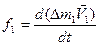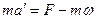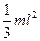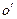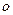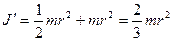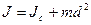Что называется уравнением движения частицы в классической механике
Понятие состояния частицы в механике. Основная задача механики.
Динамика изучает движение тел в связи с теми причинами (взаимодействия между телами), которые обуславливают тот или иной характер движения.
Основная задача динамики заключается в ответе на вопрос о том, как изменит своё состояние система при внешних воздействиях.
Для этого необходимо:
1. Установить величины, описывающие состояние физической системы.
2. Составить уравнения движения, описывающие изменения состояния системы во времени.
3. Определить физические величины, измерения которых при проведении опытов дают возможность судить о том, что происходит реально с исследуемой системой.
В классической физике состояние частицы полностью определяется координатами (x, y, z) и компонентами её скорости (vx, vy, vz) в заданный момент
времени, т. е. радиус-вектором частицы и
если m·υ·r >> h – то имеем дело с классическими законами.
Законы Ньютона. Масса. Импульс. Сила.
Первый закон Ньютона: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют законом инерции.
. Первый закон Ньютона утверждает существование инерциальных систем отсчёта.
Второй закон Ньютона: В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
где 
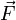
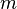
Третий закон Ньютона: Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.
Сила-есть результат взаимодействия тел, причина изменения скорости движения тел, или их деформации. F=m*a;
Масса-мера инертности тел, объект и источник тяготения.
Импульс-произведение массы тела на скорость его движения: P=m*v;
Уравнение движения частицы.
Уравне́ние движе́ния — уравнение или система уравнений, задающие закон эволюции механической или динамической системы (например, поля) во времени и пространстве.
Рассмотрим в рамках ньютоновской механики точечную частицу, способную перемещаться лишь по одной прямой (например, бусину, способную скользить по гладкой спице). Будем описывать положение частицы на прямой единственным числом — координатой — x. Пусть на эту частицу действует сила f, зависящая от положения частицы по закону Гука, то есть, выбрав удобное начало отсчета x, можем записать f = — k x. В таком случае, учитывая второй закон Ньютона и кинематические соотношения, обозначив скорость как v, будем иметь следующие уравнения движения для нашей системы:
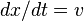
или, исключая v из системы:
Подставив начальную координату и скорость в правые части этих уравнений, и заменив бесконечно малое dt на малое, но конечное, 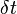

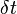
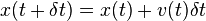
Можно увидеть, что, если 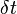
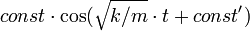
Использовав для догадки это приближенное решение или какие-то другие соображения, можем, если мы уже подозреваем, каким должно быть решение, просто подставить

где 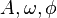
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Классическая механика
| Фундаментальные понятия |
|---|
| Пространство · Время · Масса · Сила Энергия · Импульс |
| Формулировки |
|---|
| Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби |
| Разделы |
|---|
| Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика |
| Учёные |
|---|
| Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши |
Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, это вызывающие), основанный на законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «Ньютоновской механикой».
Классическая механика подразделяется на:
Существует несколько эквивалентных способов формального математического описания классической механики:
Классическая механика даёт очень точные результаты, если её применение ограничено телами, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул. Обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными — квантовая механика. Квантовая теория поля рассматривает квантовые релятивистские эффекты.
Тем не менее, классическая механика сохраняет своё значение, поскольку:
Классическую механику можно использовать для описания движения таких объектов, как волчок и бейсбольный мяч, многих астрономических объектов (таких, как планеты и галактики), и иногда даже многих микроскопических объектов, таких как молекулы.
Классическая механика является самосогласованной теорией, то есть в её рамках не существует утверждений, противоречащих друг другу. Однако, её объединение с другими классическими теориями, например классической электродинамикой и термодинамикой приводит к появлению неразрешимых противоречий. В частности, классическая электродинамика предсказывает, что скорость света постоянна для всех наблюдателей, что несовместимо с классической механикой. В начале XX века это привело к необходимости создания специальной теории относительности. При рассмотрении совместно с термодинамикой, классическая механика приводит к парадоксу Гиббса, в котором невозможно точно определить величину энтропии, и к ультрафиолетовой катастрофе, в которой абсолютно чёрное тело должно излучать бесконечное количество энергии. Попытки разрешить эти проблемы привели к возникновению и развитию квантовой механики.
Содержание
Основные понятия
Классическая механика оперирует несколькими основными понятиями и моделями. Среди них следует выделить:
Основные законы
Принцип относительности Галилея
Законы Ньютона
Основой классической механики являются три закона Ньютона.
Первый закон устанавливает наличие свойства инертности у материальных тел и постулирует наличие таких систем отсчёта, в которых движение свободного тела происходит с постоянной скоростью (такие системы отсчёта называются инерциальными).
Второй закон Ньютона вводит понятие силы как меры взаимодействия тела и на основе эмпирических фактов постулирует связь между величиной силы, ускорением тела и его инертностью (характеризуемой массой). В математической формулировке второй закон Ньютона чаще всего записывается в следующем виде:
где 

Второй закон Ньютона может быть также записан в терминах изменения импульса тела 
В такой форме закон справедлив и для тел с переменной массой, а также в релятивистской механике.
Второго закона Ньютона недостаточно для описания движения частицы. Дополнительно требуется описание силы 
Третий закон Ньютона уточняет некоторые свойства введёного во втором законе понятия силы. Им постулируется наличие для каждой силы, действующей на первое тело со стороны второго, равной по величине и противоположной по направлению силы, действующей на второе тело со стороны первого. Наличие третьего закона Ньютона обеспечивает выполнение закона сохранения импульса для системы тел.
Закон сохранения импульса
Закон сохранения энергии
За пределами применимости законов Ньютона
Классическая механика также включает в себя описания сложных движений протяжённых неточечных объектов. Законы Эйлера обеспечивают расширение законов Ньютона на эту область. Понятие угловой момент опирается на те же математические методы, используемые для описания одномерного движения.
Уравнения движение ракеты расширяют понятие скорости, когда импульса объекта меняется со временем, чтобы учесть такой эффект как потеря массы. Есть две важные альтернативные формулировки классической механики: механика Лагранжа и Гамильтонова механика. Эти и другие современные формулировки, как правило, обходят понятие «сила», и делают упор на другие физические величины, такие как энергия или действие, для описания механических систем.
Приведенные выше выражения для импульса и кинетической энергии действительны только при отсутствии значительного электромагнитного вклада. В электромагнетизме, второй закон Ньютона для провода с током нарушается, если не включает в себя вклад электромагнитного поля в импульс системы выраженный через вектор Пойнтинга поделённый на c2, где c — это скорость света в свободном пространстве.
История
Древнее время
Классическая механика зародилась в древности главным образом в связи с проблемами, которые возникали при строительстве. Первым из разделов механики, получившим развитие стала статика, основы которой были заложены в работах Архимеда в III веке до н. э. Им были сформулированы правило рычага, теорема о сложении параллельных сил, введено понятие центра тяжести, заложены основы гидростатики (сила Архимеда).
Средние века
XIV веке французский философ Жан Буридан разработал теорию импетуса. В дальнейшем её развил ученик Жана — епископ Альберт Саксонский.
Новое время
XVII век
Динамика как раздел классической механики начал развиваться только в XVII веке. Его основы были заложены Галилео Галилеем, который первым правильно решил задачу о движении тела под действием заданной силы. На основе эмпирических наблюдений им были открыты закон инерции и принцип относительности. Помимо этого Галилеем внесён вклад в зарождение теории колебаний и науки о сопротивлении материалов.
Христиан Гюйгенс проводил исследования в области теории колебаний, в частности изучал движение точки по окружности, а также колебания физического маятника. В его работах были также впервые сформулированы законы упругого удара тел.
Заложение основ классической механики завершилось работами Исаака Ньютона, сформулировавшего в наиболее общей форме законы механики и открывшего закон всемирного тяготения. Им же в 1684 году был установлен закон вязкого трения в жидкостях и газах.
Так же в XVII веке в 1660 году был сформулирован закон упругих деформаций, носящий имя своего первооткрывателя Роберта Гука.
XVIII век
В XVIII веке зарождается и интенсивно развивается аналитическая механика. Её методы для задачи о движении материальной точки были разработаны Леонардом Эйлером, которые заложил основы динамики твёрдого тела. Эти методы основываются на принципе виртуальных перемещений и на принципе Д’Аламбера. Разработку аналитических методов завершил Лагранж, которому удалось сформулировать уравнения динамики механической системы в наиболее общем виде: с использованием обобщённых координат и импульсов. Помимо этого, Лагранж принял участие в заложении основ современной теории колебаний.
Альтернативный метод аналитической формулировки классической механики основывается на принципе наименьшего действия, который впервые был высказан Мопертюи по отношению к одной материальной точке и обобщён на случай системы материальных точек Лагранжем.
Так же в XVIII веке в работах Эйлера, Даниила Бернулли, Лагранжа и Д’Аламбера были разработаны основы теоретического описания гидродинамики идеальной жидкости.
XIX век
В XIX веке развитие аналитической механики происходит в работах Остроградского, Гамильтона, Якоби, Герца и др. В теории колебаний Раусом, Жуковским и Ляпуновым была разработана теория устойчивости механических систем. Кориолис разработал теорию относительного движения, доказав теорему о разложении ускорения на составляющие. Во второй половине XIX века происходит выделение кинематики в отдельный раздел механики.
Особенно значительны в XIX веке были успехи в области механики сплошной среды. Навье и Коши в общей форме сформулировали уравнения теории упругости. В работах Навье и Стокса были получены дифференциальные уравнения гидродинамики с учётом вязкости жидкости. Наряду с этим происходит углубление знаний в области гидродинамики идеальной жидкости: появляются работы Гельмгольца о вихрях, Кирхгофа, Жуковского и Рейнольдса о турбулентности, Прандтля о пограничных эффектах. Сен-Венан разработал математическую модель, описывающую пластические свойства металлов.
Новейшее время
В XX веке интерес исследователей переключается на нелинейные эффекты в области классической механики. Ляпунов и Анри Пуанкаре заложили основы теории нелинейных колебаний. Мещерский и Циолковский провели анализ динамики тел переменной массы. Из механики сплошной среды выделяется аэродинамика, основы которой разработаны Жуковским. В середине XX века активно развивается новое направление в классической механике — теория хаоса. Важными также остаются вопросы устойчивости сложных динамических систем.
Ограничения классической механики
Классическая механика дает точные результаты для систем, которые мы встречаем в повседневной жизни. Но её предсказания становятся некорректными для систем, скорость которых приближается к скорости света, где она заменяется релятивистской механикой или для очень малых систем, где действуют законы квантовой механики. Для систем, которые объединяют оба эти свойства, вместо классической механики применяется релятивистская квантовая теория поля. Для систем с очень большим количеством составляющих, или степеней свободы, классическая механика также не может быть адекватной, зато используются методы статистической механики.
Классическая механика является широко применяемой, потому что она, во-первых, гораздо проще и легче в применении, чем перечисленные выше теории, и, во-вторых, имеет большие возможности для аппроксимации и применения для очень широкого класса физических объектов, начиная с привычных, таких как волчок или мяч, до больших астрономических объектов (планеты, галактики) и совсем микроскопических (органические молекулы).
Хотя классическая механика является в целом совместимой с другими «классическими» теориями, такими как классическая электродинамика и термодинамика, имеются некоторые несоответствия между этими теориями, которые были найдены в конце 19 века. Они могут быть решены методами более современной физики. В частности, уравнения классической электродинамики неинвариантны относительно преобразований Галилея. Скорость света входит в них как константа, что означает, что классическая электродинамика и классическая механика могли бы быть совместимы только в одной избранной системе отсчета, связанной с эфиром. Однако, экспериментальная проверка не выявила существование эфира, что привело к созданию специальной теории относительности, в рамках которой были модифицированы уравнения механики. Принципы классической механики также несовместимы с некоторыми утверждениями классической термодинамики, что приводит к парадоксу Гиббса, согласно которому невозможно точно установить энтропию, и к ультрафиолетовой катастрофе, в которой абсолютно черное тело должно излучать бесконечное количество энергии. Для преодоления этих несовместимости была создана квантовая механика.
Основная задача динамики. Понятие состояния классической механики. Границы применимости классического способа описания движения частиц
Опр.: Динамикой называется часть механики, изучающая динамическое движение, в связи с теми причинами, которые определяют характер движения.
Такими причинами являются взаимодействия между телами.
Основная задача динамики состоит в постановке и поиске решения двух следующих задач:
1. По заданным силам (взаимодействиям) следует установить законы движения тел или точек – прямая задача.
2. По заданным законам движения вычислить силы, действующие на точки или тела – обратная задача.
В классической механике понятия состояния движения частицы в любой момент времени характеризуется положением частицы и величиной скорости. Т.о. необходимо в каждый момент времени точно знать значения координат частицы и ее скорости. При этом образом частицы является геометрическая точка, описывающая с течением времени непрерывную траекторию. Такой способ описания движения частиц имеет принципиальное ограничение.
Согласно квантовой механике, которая обобщает классическую для микромира, невозможно в каждый момент времени знать с одинаковой точностью значения координат частицы и ее скорости. Это вытекает из соотношений неопределенности Гейзенберга, имеющий следующий вид:
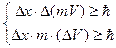
Dx – неопределенность координаты,
DV – неопределенность скорости.

2.1. Первый закон Ньютона. Понятие инерциальной системы отсчета
Если на материальную точку или тело не действуют никакие другие тела или их действие компенсируется, то тело называется свободным.
Движение свободного тела называется движением по инерции.
1 закон Ньютона описывает такое движение. Отметим, что 1 закон Ньютона содержится еще в работах Галилея. Но Ньютону принадлежит только формулировка.
Закон. Всякое тело сохраняет состояние покоя ил равномерного прямолинейного движения, если на него не действуют никакие другие тела или их действие компенсируется.
Следствие. Движение по инерции представляет собой равномерное прямолинейное движение.

Говоря о равномерном движении или состоянии покоя, необходимо учитывать систему отсчета, относительно которой рассматривается движение.
Система отсчета – совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов.
1 закон Ньютона называется законом инерции, а инерцией называется свойство тел сохранять величину и направление скорости, когда на него не действуют силы (или действуют уравновешенные силы).
ИСО является система отсчета, начало которой связано с центром Солнца, а оси направлены на неподвижные звезды (называется гелиоцентрической).
Если попытаться изменить состояние движения какого-либо тела, то тело будет при этом оказывать определенное сопротивление. Это свойство тел называется инертностью.
Количественной характеристикой инертности тела является массы.
Масса – мера инертности тела. Это скалярная физическая величина, которая измеряется в СИ в кг. Обозначается:
Для того, чтобы измерить массу какого-либо тела, необходимо эту массу сравнить с массой эталона. Например, рассмотрим взаимодействие двух тел, массами m1 и m2, в результате взаимодействия скорость первого тела изменилась на DV1, а второго на DV1. Эксперименты показывают, что всегда выполняются условия.


Если вместо m2 взять массу эталона, то по формуле (2.2) можно вычислить массу любого тела. Кроме понятия массы для дальнейшего описания потребуется описание силы.
Силой называется физическая векторная величина, характеризующая взаимодействие тел.
В настоящее время физике известно 4 вида взаимодействия, а именно:
Последние 2 взаимодействия описывают процессы в микромире. Сильное взаимодействие описывает взаимодействие между частицами внутри ядра атома. Слабое описывает процессы взаимного превращения элементарных частиц. Эти взаимодействия являются короткодействующими, проявляются на очень маленьких расстояниях. Оба они не характеризуются понятием силы. Понятие силы характерно для гравитационного и электромагнитного взаимодействий, причем в механике используются не все проявления взаимодействия, а только некоторые:
Силы гравитационного притяжения.
Проявление электромагнитного взаимодействия.
Сила упругости нити.
Сила упругости деформированного тела.
Сила реакции опоры.
1. Сила трения. Трение подразделяют на внешнее и внутреннее. 
2. Сила упругости.
3. Сила гравитационного взаимодействия. 
Для того, чтобы решить основную задачу механики, обычно приходится решать (интегрировать) уравнения движения, имеющие следующий вид:
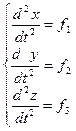
или 
Функции f1, f2, f3, f4 определяются характером взаимодействия тел и могут зависеть от координат и времени. Для того, чтобы понять откуда эти функции берутся, сформулируем 2 закон Ньютона. Существует несколько формулировок. Простейшая формулировка:
Закон. Когда на тело действует одна сила и масса тела не меняется, то ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе.

Если учесть, что ускорение вторая производная от пути, то
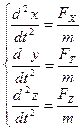
Т.о. 2 закон Ньютона представляет собой уравнение движения тела.
Более сложный случай возникает, если на тело действует несколько сил. Тогда 2 закон Ньютона имеет следующую формулировку:
Закон. Ускорение, с которым движется тело, прямо пропорционально равнодействующей всех сил и обратно пропорционально массе этого тела.
Под равнодействующей мы понимаем сумму всех сил.
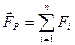

Из формулы 2 закона Ньютона получается размерность силы:
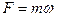
Еще более общий случай 2 закона Ньютона возникает, когда необходимо учесть возможность изменения массы тела.
Для того, чтобы сформулировать 2 закон Ньютона введем понятие импульса тела (количества движения) – это физическая векторная величина, численно равная произведению массы тела на скорость и направленная в сторону движения тела. Обозначается:

Формулировка 2 закона Ньютона имеет вид:
Закон. Скорость изменения импульса тела равна равнодействующей всех сил, действующих на это тело.
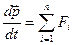
Если (2.9) подставить в (2.10), то формула приобретет следующий вид:

Если m постоянна,, то ее можно вынести за знак производной.
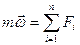
Это означает, что последняя формулировка 2 закона Ньютона является самой общей. Из нее следует другие частные случаи кроме того из этой формулировки понятие силы можно рассматривать, как просто обозначение производной по времени от импульса тела.
Это говорит о том, что сила с такой точки зрения является искусственной характеристикой, то есть можно было бы построить динамику не используя понятия сила.
Но в силу исторических традиций и потому что понятие силы достаточно удобно в динамике это понятие широко используется.
2.3. Законы Ньютона и закон сохранения импульсов
Закон Ньютона описывает взаимодействие двух тел между собой.
Он гласит: «Любые два тела взаимодействуют друг с другом с силами равными по величине, противоположными по направлению и приложены к различным телам».
Математически формулировка закона записывается
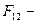

При этом эти силы приложены 

Поэтому их нельзя складывать и понятие равнодействующей этих сил не имеет смысла.
Отметим, что все три закона Ньютона, справедливы только в инерциальной системе отсчета.
Рассмотрим систему состоящую из нескольких тел, причем тела этой системы взаимодействуют только между собой – такая система тел называется ЗАМКНУТОЙ.
Эксперименты показывают, что суммарный импульс движения тел с течением времени не изменяется – ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
Математически закон сохранения импульса:

соотношение (2.12) можно получить при помощи второго и третьего закона Ньютона, если учесть, что суммарный импульс замкнутой системы находится как векторная сумма импульсов тел составляющих систему.
Рассмотрим систему состоящую из N-частиц (материальных точек). Обозначим через 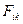
Уравнения движения всех N- частиц:
Сложим все уравнения, получится:
производная по времени.
Сумму внутренних сил можно представить в виде:
Согласно третьему закону Ньютона каждая из скобок =0 следовательно сумма внутренних сил, действующих на тела системы, всегда =0.

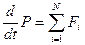
Если система замкнута, внешние силы отсутствуют и правая часть уравнения равна нулю. Соответственно 
Рассмотрим применение закона сохранения импульса к так называемому неупругому удару.
Обозначим 
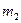



до соударения 
после соударения 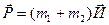
по закону сохранения импульса:
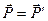
Подставим (2.13) и (2.14) в (2.15), получим:
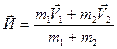
Отметим, что соотношение (2.16) это векторное соотношение, то есть в нем содержится три скалярных соотношения:
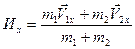
Одно из основных свойств массы, это то, что масса величина аддитивная (суммарная) это значит, что массу любого тела можно вычислить, как сумму масс частей составляющих это тело.
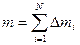
Такое разбиение бывает очень нужным в самых разнообразных случаях, один из них введение понятия центра масс.
По определению это точка, в которой сосредоточена масса всего тела (в котором можно считать сосредот.)
Для введения этого понятия тело мысленно разбивают на материальные точки, к каждой проводят r-вектор, а затем вычисляют r- вектор центра масс по формуле:
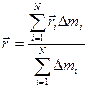
Выясним, что означают слова « в этой точке сосредоточенна масса всего тела». Это значит, что если к телу приложено множество сил к разным его точкам, то в результате, тело движется таким образом как будто к нему приложена одна сила, равная равнодействующей этих сил, причем эта сила приложена к центру масс (инерции) это утверждение называется ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС.
Докажем ее. Для этого, для каждой материальной точки запишем второй закон Ньютона:

Суммируем уравнения из системы (2.19)
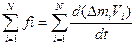
Учтем, что скорость 


Меняя местами операции суммирования и дифференцирования:
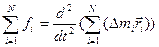
Выражение правой части под знаком суммы это числитель формулы r- вектора для центра масс. Поэтому можно формулу (2.23) преобразуем следующим образом. Умножить и разделить выражение под знаком производной на то выражение, которое стоит в знаменателе для r- вектора центра масс.
Теперь под знаком второй производной находится r- вектор центра масс.

В левой части (2.24) находится равнодействующая всех сил действующих на тело. В правой части произведение всей массы тала на ускорение точки центра масс (инерции).
точка с – обозначает центр масс тела ч.т.д. Во многих задачах бывает удобно проводить решения в такой системе отсчета, в которой центр масс (инерции) покоится, называется система центра инерции (СЦИ).
2.4. Неинерциальные системы отсчета. Сила инертности
В неинерциальной системе отсчета (НИСО), движущейся по отношению к инерциальным системам с ускорением тело будет иметь ускорение а, отличное от нуля. Поскольку в ИСО F=0, равенство F=ma не соблюдается. Система к является инерциальной. Показанные r – векторы связаны соотношением

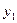
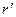
0
0
Двухкратное дифференцирование этого соотношения по времени приводит к

а- ускорение частицы в системе 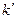
Умножим равенство 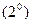
Использовав обозначение силы инертности, напишем уравнение
2.5. Момент силы и момент импульса. Уравнения движения и равновесия твердого тела (уравнеие моментов)
Важные законы динамики твердого тела связаны с положением момента силы. Существуют два различных понятия: момент силы, относительно точки, момент силы, относительно оси.
1. Пусть О некоторая точка, относительно которой вводится момент силы 
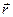
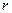
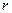
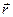
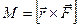


то есть направление моиента силы, находится по правилу векторного произведения, то есть все три вектора взаимно перпендикулярны. Мы ввели понятие момент силы, относительно точки О.
Если через точку О проходит оси координат, то проекциями момента силы будут 
Они будут моментами силы относительно этих осей. В том случае когда необходимо находить момент нескольких сил относительно точки можно просто векторно сложить момент исходных сил. В том случае, когда линии действия сил лежат в одной плоскости, то момент этих сил относительно этой точки будет равен моменту равнодействующей этих сил относительно точки. Аналогично вводится понятие момента импульса относительно точки и момент импульса относительно оси.


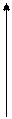

Пусть имеется материальная точка обладающая импульсом р, тогда моментом импульса относительно некоторой точки О, будет физическая величина равная векторному произведению 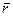

Моментом импульса относительно оси будет проекция вектора момента импульса относительно точки на ось проходящую через эту точку. Получим уравнение моментов для одной материальной точки. Для этого продифференцируем по времени соотношение (2.27)




Подставляя эти уравнения в (2.28)
уравнение моментов 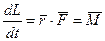
Где мы учли, что
Уравнение связывает между собой момент силы действующей на материальную точку и скорость изменения момента импульса. Нетрудно увидеть, что формулы (2.31) и (2.32) очень похожи. (2.31) выражает второй закон Ньютона, поэтому можно утверждать, что (2.32) тоже выражает второй закон Ньютона, записанный для моментов, то есть для вращательного движения. Если на твердое тело или точку внешние силы не действуют, или действуют таким образом, что их суммарный момент равен нулю, то тело или точка будут находиться в состоянии равновесия. Таким образом для тела или точки способных вращаться относительно некоторой точки или оси, уравнение равновесия будут иметь вид:

2.6. Момент инерции тела относительно оси
Рассмотрим простейший случай вращательного движения твердого тела, а именно, когда имеется одна ось вращения ОО и тело вращается вокруг этой оси. В этом случае все точки тела движутся по окружностям, центры которой лежат на оси вращения, а радиусами окружности является расстояние от оси вращения до данной точки.
 |
В этом случае моментом импульса относительно оси ОО, будет проекция момента импульса относительно любой точки лежащей на оси вращения на эту ось. Величина момента импульса относительно оси будет находиться:
Такую формулу можно записать для любой материальной точки данного тела если масса материальной точки 
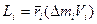
В данном случае 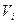

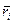
Если свести угловую скорость

Подставим (2.36) в (2.35) получим

Введем новую физическую величину момент инерции (J) для материальной точки эта величина находится по формуле:

С учетом (2.38) выражение для момента импульса

Если просуммировать соотношение (2.39) по всем индексам i, то получим:

В левой части (2.40) находится момент импульса всего тела, а в правой части произведение угловой скорости на момент инерции всего тела:
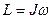
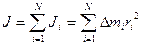
Формула (2.42) выражает значение момента инерции для любого мела, в общем случае эта формула приближенная, и она будет тем точнее, чем на более мелкие части мы разбиваем тело.
В пределе при 
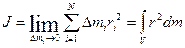
Если ввести понятие плотности, то
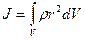
Рассмотрим, как находятся моменты инерции некоторых тел простых конфигураций.
Вывод для стержня, шара, диска.
Сплошной цилиндр (диск)
Шар
Прямой тонкий стержень 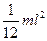
Стержень, ось перпендикулярна к стержню и проходит через его конец
Сфера, ось проходит через центр 
Установим законы механики, связывающие величины, характеризующие вращательное движение.
Пусть потенциальная энергия тела остается неизменной 

В соответствии с определение работы имеем:
так как 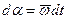
Из этого выражения легко получается закон:
который похож на второй закон Ньютона. Он называется ОСНОВНЫМ ЗАКОНОМ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ:
момент силы, действующий на тело, есть величина, численно равная произведению момента инерции тела на его угловое ускорение.
Как и во втором законе Ньютона, можно учесть зависимость момента инерции тела от времени, и запишем в виде:
2.7. Вращательный момент и момент импульса основной закон динамики вращательного движения
Т.о. момент инерции зависит от:
2. геометрической формы тела
4. от положения оси вращения.
Последнее обстоятельство учитывается при помощи теоремы Штейнера.
Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси проходящей через центр масс параллельно данной и произведению массы тела на квадрат расстояния между осями.

Доказать теорему самостоятельно, расстояние между а равно радиусу цилиндра r. Следовательно для однородного цилиндра:
Стержень можно считать тонким, если max поперечный размер его много меньше длины l, следовательно
С помощью этой теоремы можно найти момент инерции 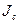
откуда 
Момент инерции J относительно оси О определяется выражением
Разобьем это выражение на три суммы:
Первая сумма представляет собой момент инерции 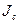


Дата добавления: 2016-04-19 ; просмотров: 5738 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ