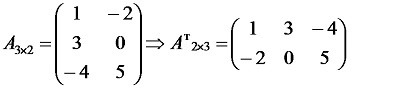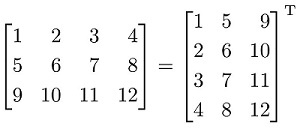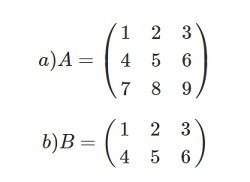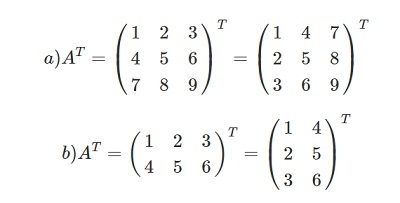Что называется транспонированием матрицы

Транспонирование матрицы

Обновлено: 19 Июля 2021

Нам уже знакомо понятие матрицы. Этот математический объект имеет прикладное значение: он позволяет структурировать числа и информацию, проводить сложные расчёты. С ним можно проделывать различные операции, и одной из них является транспортирование.

Что такое транспонированная матрица, в чем отличие от обычной

Транспонирование – это алгоритм, при котором m-строки меняются местами с n-столбцами.

Транспонированная матрица, в отличие от обычной, помогает получить одинаковый результат при умножении на вектор-столбец и вектор-строку, что значительно упрощает дальнейшие математические вычисления.

Особенности, определитель и свойства целочисленных

Свойства транспортирования целочисленных матриц:

Если матрица А – квадратная (m=n), то определитель исходной и транспортированной матрицы равны: det A T = det A.

Напомним, что определитель – это некоторое число, с которым можно сравнить любую квадратную матрицу.

Формула, как обозначается транспонированная матрица

Тогда формула для транспортировки выглядит следующим образом:

A T ij = A ji

Формально, если А = m × n, то A T = n × m, но математически это записывается через индексы i и j.

Примеры задач на транспонирование матриц

Само транспортирование – довольно лёгкий процесс. Рассмотрим один пример.

Задача: даны А = (m × n) и В = (m × n).

Необходимо выполнить транспортирование.

Произведение и сумма транспонированных матриц

Теорема: транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.

В математическом виде теорема выглядит так:

С T = (A · B) T = В T · А T

Сумма вычисляется по аналогичной формуле:

C T = (A + B) T = A T + В T

Периодически возникают сложности с учебой? ФениксХэлп может помочь!

Источник

Математика для чайников. Матрицы и основные действия над ними

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Источник

Свойства транспонированных матриц

2. Двукратное транспонирование не изменяет матрицу (A T ) T = A.

6. Если транспонированная матрица A T совпадает с данной матрицей A, то матрица A называется симметричной.

1.3. Обратная матрица

Матрица называется обратной к данной матрице A, если их произведение равно единичной матрице:

.

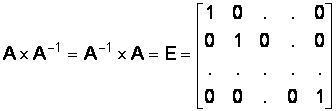
Вырожденной квадратной матрицей называется такая матрица, определитель которой равен нулю.

Матрица, определитель которой не равен 0, называется невырожденной.

Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной. Для вычисления обратной матрицы к матрице А составим матрицу А* (присоединенную) из алгебраических дополнений матрицы А:

.

Матрицу транспонируем и каждый элемент разделим на определитель |A|. Нетрудно показать, что построенная таким образом матрица будет обратной к матрице А [6]:

.

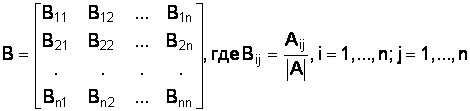
F Пример 1.4. Дана матрица А. найти обратную матрицу при помощи MS Excel.

.

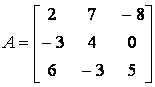
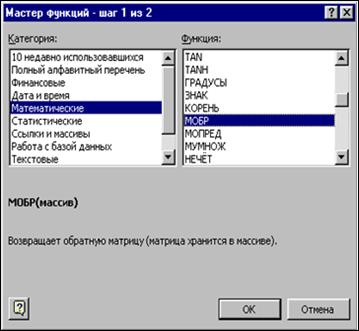
В нашем случае матрица А находится в ячейках B1:D3. Для нахождения обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы, пусть в нашем случае это будут ячейки G1:E3. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР(), предназначенную для вычисления обратной матрицы (рис. 1.9), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций.

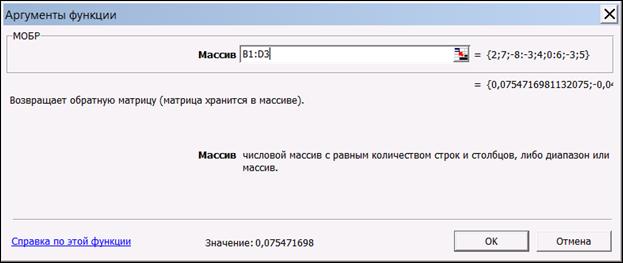
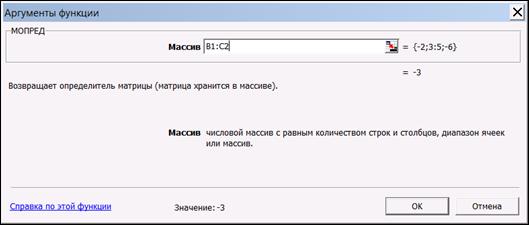
В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив (рис. 1.10). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица – в нашем случае B1:D3. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.

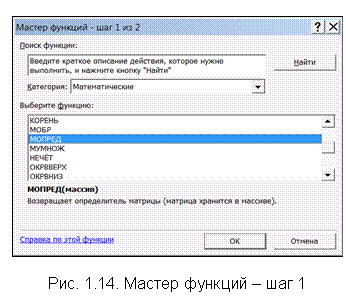
Рис. 1.9. Мастер функций – шаг 1

Рис. 1.10. Мастер функций – шаг 2

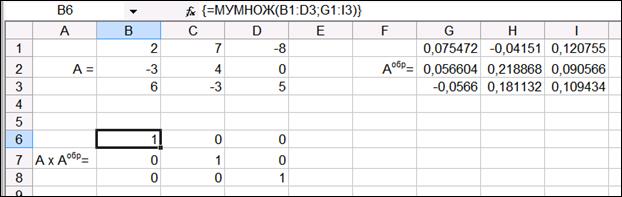
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного диапазона под обратную матрицу появится некое число. Чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид, изображенный на рис. 1.11.

Рис. 1.11. Пример вычисления обратной матрицы

Для того чтобы проверить, правильно ли найдена обратная матрица, необходимо умножить матрицу A на А обр и получить в результате единичную матрицу. В результате проведенных вычислений рабочий лист примет вид, изображенный на рис. 1.12.

Рис. 1.12. Проверка правильности решения.

1.4. Сложение матриц

Суммой матриц A = (a_ij) и B(b_ij) одной и той же размерности (mⅹn) называется матрица того же размера C = (c_ij), каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя [6].

F Пример 1.5. Сложить матрицы А и В при помощи MS Excel.

.

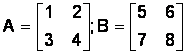
Введем исходные данные на рабочий лист. Для сложения матриц А и B выделим диапазон E4:F5 и введем формулу =B1:C2+F1:G2(рис. 1.13). Вычитание матриц выполняется аналогично. Для получения результата в обоих случаях необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.

Рис. 1.13. Пример сложения матриц

Свойства сложения матриц:

Если О – нулевая матрица размера mⅹn, то A+O = A; A+(-A) = O.

Матрица С = А+(-В) называется разностью матриц А и В и записывается в виде С = А-В [7].

Мы видим, что квадратные матрицы порядка n можно складывать, вычитать и перемножать.

1.5. Вычисление определителей

Пусть A = (a_ij) (i, j = 1, …, n) – квадратная матрица порядка n. Определителем (или детерминантом) матрицы A называется число, которое ставится в соответствие этой матрице и может быть вычислено по ее элементам. Простейший пример использования детерминанта – выяснение возможности обращения матрицы исходя из значения ее детерминанта. Если детерминант матрицы равен нулю, обратить ее невозможно.

Операция вычисления детерминанта определена только для квадратных матриц. Определители являются основными числовыми характеристиками квадратных матриц [7].

Определителем (детерминантом) матрицы A=(a₁₁), состоящей из одного числа a₁₁, называется само это число.

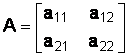
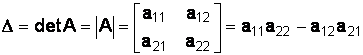
Определителем матрицы второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:

.

Рассмотрим матрицу третьего порядка:

.

Определителем матрицы A третьего порядка называется число

.

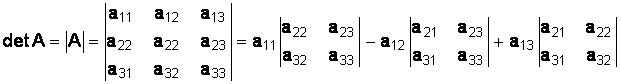
Данная формула называется формулой разложения определителя
3-го порядка по элементам первой строки [6].

Для вычисления детерминанта матрицы в Excel используется функция массива МОПРЕД().

F Пример 1.6. Вычислить определители заданных матриц:

1.6.1. .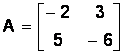

.

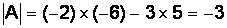
1.6.2. .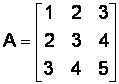

.

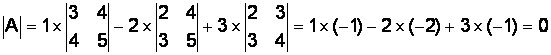
1.6.3. .

.

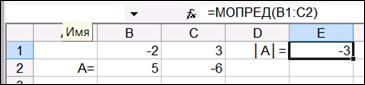
Решим примеры при помощи пакета MS Excel. Матрица А находится в ячейках B1:C2. Для нахождения определителя матрицы необходимо перейти в свободную ячейку и обратиться к Мастеру функций. В категории Математические выберем функцию МОПРЕД(), предназначенную для вычисления определителя матрицы (рис. 1.14), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций.

В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив (рис. 1.15) Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица, в нашем случае B1:С2.

Если поле Массив заполнено, можно нажать кнопку OK. В ячейке, выделенной под определитель матрицы, появится решение для первого примера, что соответствует представленному решению примера 1.6.1 (рис. 1.16).

Рис. 1.15. Мастер функций – шаг 2

Рис. 1.16. Вычисления определителя для примера 1.6.1

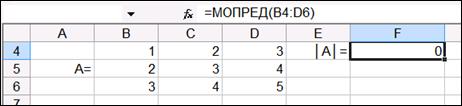
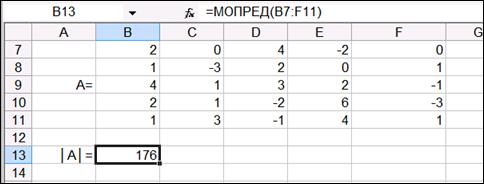
Аналогично проводим вычисления для примеров 1.6.2 и 1.6.3 (рис. 1.17 и 1.18). Применяя пакет MS Excel, сделаем проверку уже решенным примерам.

Рис.1.17. Вычисления определителя для примера 1.6.2

Рис. 1.18. Вычисления определителя для примера 1.6.3

Определитель n-го порядка.

Определителем квадратной матрицы порядка n называется число:

.

Источник

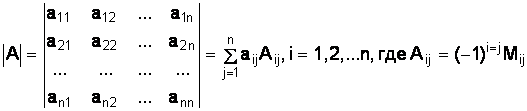
Транспонированная матрица

Транспонированная матрица — матрица , полученная из исходной матрицы заменой строк на столбцы.

Формально, транспонированная матрица для матрицы размеров — матрица размеров , определённая как A T [i, j] = A[j, i].

и

Свойства транспонированных матриц

Связанные определения

Отсюда следует, что элементы главной диагонали такой матрицы (могут) равняются нулю.

См. также

Полезное

Смотреть что такое «Транспонированная матрица» в других словарях:

транспонированная матрица — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] транспонированная матрица Результат операции транспонирования, т.е. перемены местами столбцов и строк исходной матрицы. Если исходная матрица [aij],… … Справочник технического переводчика

Транспонированная матрица — [transposed matrix] результат операции транспонирования, т.е. перемены местами столбцов и строк исходной матрицы. Если исходная матрица [aij], то транспонированная по отношению к ней записывается [aji] … Экономико-математический словарь

транспонированная матрица — матрица, получающаяся из данной (прямоугольной или квадратной) матрицы А = ||aik|| после замены строк соответствующими столбцами. Обозначение транспонированной матрицы А = ||a ik||, где a ik = aki для любых i и k. * * * ТРАНСПОНИРОВАННАЯ МАТРИЦА … Энциклопедический словарь

транспонированная матрица — transponuotoji matrica statusas T sritis fizika atitikmenys: angl. transposed matrix vok. transponierte Matrix, f rus. транспонированная матрица, f pranc. matrice transposée, f … Fizikos terminų žodynas

ТРАНСПОНИРОВАННАЯ МАТРИЦА — матрица, получающаяся из данной (прямоуг. или квадратной) матрицы А= |aik| после замены строк соотв. столбцами. Обозначение Т. м. А = ||а ik||, где a ik= од для любых i и k … Естествознание. Энциклопедический словарь

Транспонированная матрица — (нем. transponieren перекладывать, от лат. transpono переставляю) Матрица, получающаяся из данной (прямоугольной или квадратной) матрицы А = II a ik II после замены строк соответствующими столбцами. Обозначение Т. м. A = II a ik II, где a … Большая советская энциклопедия

матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. [http://www.vidimost.com/glossary.html] матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика

Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь

Источник

Транспонирование матрицы, формулы и примеры

В этом уроке мы рассмотрим операцию “транспонирование матрицы” и как она выполняется на Python. Также разберем на примерах свойства этой операции.

Транспонирование матрицы

Транспонирование матрицы – это процесс замены строк матрицы на ее столбцы, а столбцов соответственно на строки. Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T.

Для исходной матрицы:

Транспонированная будет выглядеть так:

Решим задачу транспонирования матрицы на Python. Создадим матрицу A:

>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> print(A)
[[1 2 3]
[4 5 6]]

Транспонируем матрицу с помощью метода transpose():

>>> A_t = A.transpose()
>>> print(A_t)
[[1 4]
[2 5]
[3 6]]

Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:

Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.

Свойство 1. Дважды транспонированная матрица равна исходной матрице:

>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> print(A)
[[1 2 3]
[4 5 6]]

Свойство 2. Транспонирование суммы матриц равно сумме транспонированных матриц:

>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> B = np.matrix(‘7 8 9; 0 7 5’)
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
[[ 8 4]
[10 12]
[12 11]]
>>> print(R)
[[ 8 4]
[10 12]
[12 11]]

Свойство 3. Транспонирование произведения матриц равно произведению транспонированных матриц расставленных в обратном порядке:

>>> A = np.matrix(‘1 2; 3 4’)
>>> B = np.matrix(‘5 6; 7 8’)
>>> L = (A.dot(B)).T
>>> R = (B.T).dot(A.T)
>>> print(L)
[[19 43]
[22 50]]
>>> print(R)
[[19 43]
[22 50]]

В данном примере, для умножения матриц, использовалась функция dot()из библиотеки Numpy.

Свойство 4. Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:

>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> k = 3
>>> L = (k * A).T
>>> R = k * (A.T)
>>> print(L)
[[ 3 12]
[ 6 15]
[ 9 18]]
>>> print(R)
[[ 3 12]
[ 6 15]
[ 9 18]]

>>> A = np.matrix(‘1 2; 3 4’)
>>> A_det = np.linalg.det(A)
>>> A_T_det = np.linalg.det(A.T)
>>> print(format(A_det, ‘.9g’))
-2
>>> print(format(A_T_det, ‘.9g’))
-2

Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.9g’).

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками.

Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Транспонирование матрицы в программе Microsoft Excel

При работе с матрицами иногда нужно их транспонировать, то есть, говоря простыми словами, перевернуть. Конечно, можно перебить данные вручную, но Эксель предлагает несколько способов сделать это проще и быстрее. Давайте разберем их подробно.

Процесс транспонирования

Транспонирование матрицы – это процесс смены столбцов и строк местами. В программе Excel имеется две возможности проведения транспонирования: используя функцию ТРАНСП и при помощи инструмента специальной вставки. Рассмотрим каждый из этих вариантов более подробно.

Способ 1: оператор ТРАНСП

Функция ТРАНСП относится к категории операторов «Ссылки и массивы». Особенностью является то, что у неё, как и у других функций, работающих с массивами, результатом выдачи является не содержимое ячейки, а целый массив данных. Синтаксис функции довольно простой и выглядит следующим образом:

Чтобы решить данную проблему, выделяем весь транспонированный диапазон. Переместившись во вкладку «Главная» щелкаем по пиктограмме «Копировать», которая расположена на ленте в группе «Буфер обмена». Вместо указанного действия можно после выделения произвести набор стандартного сочетания клавиш для копирования Ctrl+C.

Вслед за этим формула массива ТРАНСП будет удалена, а в ячейках останутся только одни значения, с которыми можно работать так же, как и с исходной матрицей.

Урок: Мастер функций в Экселе

Способ 2: транспонирование матрицы с помощью специальной вставки

Кроме того, матрицу можно транспонировать с помощью одного элемента контекстного меню, который носит название «Специальная вставка».

Вместо этого можно сделать и по-другому. Выделив область, кликаем по ней правой кнопкой мыши. Активируется контекстное меню, в котором следует выбрать пункт «Копировать».

В виде альтернативы двум предыдущим вариантам копирования, можно после выделения произвести набор комбинации горячих клавиш Ctrl+C.

Этими же двумя способами, о которых шла речь выше, можно транспонировать в Excel не только матрицы, но и полноценные таблицы. Процедура при этом будет практически идентичной.

Урок: Как перевернуть таблицу в Экселе

Итак, мы выяснили, что в программе Excel матрицу можно транспонировать, то есть, перевернуть, поменяв столбцы и строчки местами, двумя способами. Первый вариант предполагает использование функции ТРАНСП, а второй – инструменты специальной вставки.

По большому счету конечный результат, который получается при использовании обоих этих способов, ничем не отличается. Оба метода работают практически в любой ситуации. Так что при выборе варианта преобразования, на первый план выходят личные предпочтения конкретного пользователя.

То есть, какой из данных способов для вас лично удобнее, тот и используйте.

Мы рады, что смогли помочь Вам в решении проблемы.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Действие третье. Транспонирование матрицы

Пошаговый пример: Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное. НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Таким образом, переставлять матрицы в произведении нельзя!

Транспонирование матрицы и таблицы в Excel

Зачастую у нас в работе возникает необходимость перевернуть данные — из строк сделать столбцы и наоборот.
Рассмотрим различные способы транспонирования матрицы или таблицы в Excel.

Предположим, что у нас имеется следующая матрица, которую мы хотим транспонировать:

Разберем 2 способа транспонирования матрицы в Excel: с помощью специальной вставки и с помощью функции ТРАНСП.

Способ 1. Транспонирование с помощью специальной вставки

Чтобы транспонировать матрицу выделяем диапазон ячеек A2:C5, в котором находится матрица.
Нажимаем правой кнопкой мыши на выделенный диапазон и в всплывающем окне выбираем Копировать (или нажимаем комбинацию клавиш Ctrl + C).

Элементы транспонированной матрицы представляют собой вставленные значения, другими словами полученная транспонированная матрица не является динамической и при изменении элементов исходной матрицы элементы транспонированной меняться не будут.
Чтобы этого избежать воспользуемся другим инструментом Excel — функцией ТРАНСП.

Способ 2. Транспонирование с помощью функции ТРАНСП

Синтаксис и описании функции транспонирования:

ТРАНСП(массив)
Преобразует вертикальный диапазон ячеек в горизонтальный, или наоборот.

Выделим диапазон пустых ячеек E2:H4, в которых будет находиться транспонированная матрица.
Не снимая выделения с пустых ячеек вводим формулу ТРАНСП и в качестве аргумента функции выбираем диапазон ячеек A2:C5, который нужно транспонировать:

После ввода формулы =ТРАНСП(A2:C5) нажмите Ctrl + Shift + Ввод, чтобы применить формулу массива ко всем выделенным ячейкам.
В результате получаем транспонированную матрицу:

Удачи вам и до скорой встречи на страницах блога Tutorexcel.ru!

Источник