Что называется степенью статической неопределимости

Степень статической неопределимости

Вы будете перенаправлены на Автор24

Степень статической неопределимости – это разность между количеством неизвестных усилий и числом независимых уравнений равновесия, которые можно составить для данной системы.

Стержневые системы

Стержневая система с точки зрения строительной механики – это конструкция, воспринимающая нагрузки и состоящая из стержней, шарнирно или жестко сопряженных друг с другом. Если элементы такой конструкции работают только на растяжение или только на сжатие, то такую конструкцию называют фермой.

Ферма состоит из прямых стержней, шарнирно соединенных между собой. Для ферм характерно приложение внешних усилий в узлах (местах примыкания двух и более стержней).

Если какой-либо стержневой элемент конструкции работает в большей мере на изгиб, то такая система называется рамой.

Если все элементы шарнирно-стержневой системы, а также приложенные к ней нагрузки располагаются в одной плоскости, то такая система называется плоской.

Если элементы стержневой системы расположены в одной плоскости, а внешние усилия, включая реакции опор, приложены в перпендикулярной плоскости, то такая система называется плоскопространственной. Стержневые системы, не относящиеся ни к одной из вышеописанных категорий, называются пространственными.

Рисунок 1. Шарнирно-стержневые системы. Автор24 — интернет-биржа студенческих работ

Любую шарнирно-стержневую систему принято разделять на статически определимую и статически неопределимую. Под статически определимой системой понимается такая система, в которой усилия во всех элементах могут определяться методом сечений с применением только уравнений равновесия. В случаях, когда выполнить подобный расчет невозможно – систему называют статически неопределимой.

Готовые работы на аналогичную тему

Связи и статическая неопределимость

Под степенью статической неопределимости понимается разность между количеством неизвестных усилий (например, реакций опор или внутренних силовых факторов) и числом независимых уравнений равновесия, которые можно составить для данной системы.

Связи, наложенные на шарнирно-стержневую систему, могут быть внешними и внутренними. Внешние связи – это ограничения, накладываемые на абсолютные перемещения узлов или сечений системы. Внутренние же связи ограничиваются относительными перемещениями элементов системы. Отсюда следует, что статическая неопределимость системы может быть вызвана как внутренними, так и внешними связями.

Если речь идет о внешних связях, то положение жесткого тела в некоторой плоскости x, y может характеризоваться тремя независимыми параметрами (двумя координатами и углом поворота рассматриваемой плоскости). Следовательно, необходимое для равновесия системы число связей будет равно трём (исходя из количества уравнений равновесия: Σx = 0, Σy = 0 и Σm = 0).

Если некая плоская система состоит из D частей, каждая из которых может быть рассмотрена как жесткое тело, то количество параметров, необходимых для определения положения данной системы будет равно 3D. Каждый шарнир, соединяющий две части системы, разрешает только взаимный поворот этих двух частей. Как следствие, шарнир устраняет возможность взаимного смещения частей системы. Это значит, что введением шарнира можно уменьшить количество возможных перемещений системы на две единицы. Помимо этого, каждый опорный стержень устраняет возможность смещения системы в соответствующем направлении.

Анализируя вышеописанное, можно подсчитать степень статической неопределимости (определяемую внешними связями):

Здесь D – количество дисков (частей) анализируемой системы, каждый из которых может рассматриваться как абсолютно жесткое тело. Ш – количество шарниров в системе, соединяющих диски. С – количество опорных стержней. Статически определимой системой можно назвать такую, при которой W = 0. При W

На рисунке изображены наиболее характерные типы внешних связей и их схематичное изображение. В первом случае (а) плоская рама имеет три внешние связи, во втором (б) – пять. Это означает, что в первом случае шарнирно-стержневая конструкция имеет необходимое для статической определимости количество шарниров и стержней.

Во втором случае система имеет две дополнительные внешние связи. Интересно, что в обоих случаях рама будет статически неопределимой, поскольку ее конфигурация не позволяет определить усилия во всех стержнях с использованием уравнений статики. Поэтому для окончательного ответа на вопрос о статической определимости необходимо проанализировать совместно наложенные и внутренние связи системы.

Методики расчета статически неопределимых систем основываются на определении перемещений её узлов. Вышеизложенный метод также имеет свое название – метод начальных параметров. При всех достоинствах данного метода он обладает весьма существенным недостатком – в случае большого количества расчетных участков вычислительные формулы становятся очень громоздкими. Максимально отрицательно это сказывается на расчетах криволинейных стержневых систем.

В этой связи следует упомянуть более универсальный метод расчета статически неопределимых систем – метод Мора. Для определения линейного или углового перемещения он предполагает рассмотрение системы в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается путем удаления заданных нагрузок и приложения единичного усилия (F = 1) в том месте, где требуется определить перемещение. В местах, где требуется определить линейное перемещения (например, прогиб балки или элемента рамы) прикладывают сосредоточенную силу (F = 1). Если необходимо найти угол поворота узла, то прикладывать следует сосредоточенную пару сил (M = 0).

Источник

Статически неопределимые системы

Вы будете перенаправлены на Автор24

Сущность статически неопределимых систем

Статически неопределимая система – это геометрически неизменяемая система, в которой усилия в опорах, стержнях и т.д. не могут определяться с помощью одних лишь уравнений статики. Такие системы требуют совместное рассмотрение статических уравнений равновесия совместно с дополнительными уравнениями, которые характеризуют деформации системы.

Статически неопределимая система характеризуется наличием «лишних» связей, которые допускается удалить, не нарушив при этом геометрической неизменяемости системы. Количество дополнительных уравнений, которые следует составить для определения усилий, будет равно числу «лишних» связей (лишних неизвестных). Данное число еще называют степенью статической неопределимости системы, о ней также пойдет речь в настоящей статье. Для определения усилий в подобных системах чаще всего используют метод сил и метод перемещений. Метод сил также используется при механизированном расчете строительных конструкций.

Из вышеизложенного следует, что степень статической неопределимости системы может быть найдена по формуле:

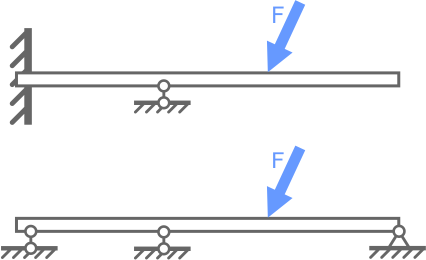
В качестве примера можно рассмотреть случай с заделанной с одной стороны консольной балкой. Поскольку в такой опоре существует три опорные реакции, данная система будет являться статически определимой, ведь из курса теоретической механики известно, что для плоской системы сил можно составить только три уравнения равновесия.

Если добавить к вышеописанной системе еще одну опору, например, шарнирно-подвижную, то такая балка становится статически неопределимой один раз, поскольку количество неизвестных увеличивается до четырех, а уравнений равновесия для данного случая можно составить только три.

Готовые работы на аналогичную тему

Таким образом, если к рассматриваемой системы прибавлять последовательно по одной опоре, то степень статической неопределимости также будет увеличиваться на единицу. В таких случаях для определения величины и направления неизвестных усилий потребуется составление дополнительных уравнений.

Процесс определения усилий в «лишних» связях системы называют раскрытием статической неопределимости. Существует ряд способов раскрытия статической неопределимости, их принцип основан на двух положениях. Первое основано на равенстве нулю соответствующих точек системы на ее опорах, второе – на совместности деформаций всех или нескольких элементов системы.

Степень статической неопределимости

Следует заметить, что перед расчетом любой системы методами строительной механики необходимо определить степень статической неопределимости этой системы. Как уже упоминалось выше, для простейших систем (балок и элементарных рам) степень статической неопределимости будет равна числу «лишних» связей.

Дополнительные связи в системах можно удалить, не нарушив при этом их геометрической неизменяемости. Особенностью большинства этих связей является то, что реакции от внешних усилий в них определить нельзя с помощью одних лишь уравнений статики. Такие связи называют условно необходимыми. Наряду с ними в системах часто имеются связи, усилия в которых можно определить из условий равновесия. Такие связи называют абсолютно необходимыми. Удаление этих связей приводит к преобразованию системы в геометрически неизменяемую или мгновенно изменяемую.

Следует различать внешне и внутренне статически неопределимые системы. Первые представляют собой системы, в которых имеются только «лишние» внешние связи (например, опорные закрепления). Внутренне статически неопределимыми называют системы, обладающие «лишними» связями, которые обычно вводятся для взаимного соединения частей системы.

Однако, для определения степени статической неопределимости сложной системы следует понимать разницу между простым и сложным шарниром. Простым называют шарнир, соединяющий два стержневых элемента. Шарнир, соединяющий три и более стержня, называют сложным. Количество простых шарниров в системе можно определить по формуле:

Ш = СТ – 1,

где СТ – количество стержневых элементов в узле.

Источник

iSopromat.ru

Статически неопределимыми называют системы, в которых для определения опорных реакций либо внутренних усилий одних только уравнений статики недостаточно.

Статическая неопределимость возникает из-за наличия дополнительных или «лишних» связей.

Здесь под словом «лишние» понимаются дополнительные опоры (связи) добавление которых не влияет на геометрическую неизменяемость системы в целом.

Дополнительные опоры увеличивают прочность и жесткость систем, что позволяет делать их более экономичными.

Степень статической неопределимости систем

Степень статической неопределимости n определяется по формуле:

где,
k – количество неизвестных усилий (реакций связи),
m – количество уравнений равновесия которые можно составить для данной системы.

Системы, для которых n=1 называют однажды статически неопределимыми, n=2 – дважды СН и т.д.

Примеры статически неопределимых систем

В качестве примера рассмотрим следующий случай:

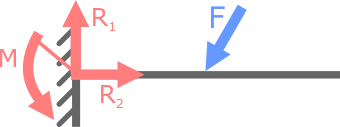
Консольная балка, закрепленная только в жесткой заделке – статически определима, так как в опоре данной схемы могут иметь место не более трех опорных реакций (вертикальная и горизонтальная силы и момент).

Как известно из курса теоретической механики для плоской системы сил можно составить только три уравнения равновесия. Трех уравнений для определения трех неизвестных вполне достаточно.

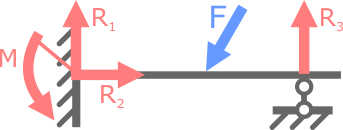
Теперь, если добавим к рассматриваемой схеме еще одну опору, например шарнирно-подвижную, то балка становится статически неопределимой, так как количество неизвестных связей увеличилось до четырех, а уравнений равновесия по-прежнему можно составить только три.

В данном случае для расчета опорных реакций не хватает еще одного уравнения, т.е. система один раз (однажды) статически неопределима.

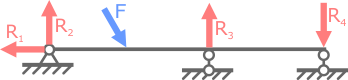
Если к данной системе последовательно добавлять опоры, то степень неопределимости также будет возрастать.

В таких случаях для расчета величины и направления неизвестных усилий потребуются дополнительные уравнения.

Другие примеры СНС

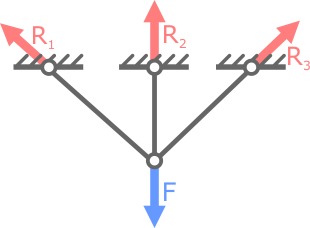
Примеры однажды статически неопределимых систем (n=1):

Статически неопределимая стержневая система

Раскрытие статической неопределимости

Расчет усилий в лишних связях называется раскрытием статической неопределимости системы.

Существует несколько способов раскрытия статической неопределимости, принцип которых основан на:

Наиболее универсальным из них является метод сил.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Что называется степенью статической неопределимости

Как уже известно, при расчете некоторых стержневых систем для определения усилий в них недостаточно использовать одни лишь уравнения статики, а необходимо составлять дополнительные уравнения — уравнения деформаций (перемещений). Такие системы называются статически неопределимыми.

В настоящей главе рассмотрены расчеты плоских статически неопределимых стержневых систем. Аналогичными способами рассчитывают и пространственные статически неопределимые системы.

Характерной особенностью статически неопределимых систем (в отличие от статически определимых) является то, что распределение усилий в них зависит не только от внешних сил, но и от соотношений между поперечными размерами отдельных элементов. Если элементы систем изготовлены из различных материалов, то распределение усилий также зависит от модулей упругости этих материалов (см. § 9.2).

Расчет статически неопределимой системы начинают с анализа ее схемы. Анализ необходим прежде всего для того, чтобы установить степень статической неопределимости.

Степень статической неопределимости равна числу лишних связей, удаление которых превращает статически неопределимую систему в статически определимую, геометрически неизменяемую систему.

Геометрически неизменяемой называется такая система, изменение фермы которой возможно лишь в связи с деформациями ее элементов.

Статически определимая система не имеет ни одной лишней связи; удаление из нее хотя бы одной связи превращает ее в геометрически изменяемую систему, т. е. в механизм.

Балка, показанная на рис. 1.12, а, является системой, один раз (или однажды) статически неопределимой, так как один из опорных стержней представляет собой лишнюю (избыточную) связь балки с опорой (с основанием).

Отбросив один из опорных стержней (рис. 1.12, б) или включив в балку один шарнир (рис. 1.12, в), получим статически определимую, геометрически неизменяемую систему.

Систему, состоящую из ряда элементов (прямых или криволинейных), жестко (без шарниров) связанных между собой и образующих замкнутую цепь, будем называть замкнутым контуром.

Прямоугольная рама, изображенная на рис. 2.12, я, представляет собой замкнутый контур. Она трижды статически неопределима, так как для превращения ее в статически определимую необходимо, например, перерезать один из ее элементов (рис. 2.12, б) и тем самым устранить три лишние связи. Реакциями этих связей являются продольная сила, поперечная сила и изгибающий момент, действующие в месте разреза; их нельзя определить при помощи уравнений статики. В аналогичных условиях в смысле статической неопределимости находится любой замкнутый контур, который всегда трижды статически неопределим.

Примером сооружения с одним замкнутым контуром является также система, изображенная на рис. 3.12, а. Замкнутым контуром является и бесшарнирная рама, изображенная на рис. 3.12, б; она ограничена снизу землей, которую можно рассматривать как бесконечно жесткий стержень.

В рамной конструкции, представленной на рис. 4.12, а, верхний контур снабжен шарниром; в разрезе, проведенном по этому шарниру, действуют только два внутренних усилия: N и Q (рис. 4.12, б). Такой контур дважды статически неопределим. Если рассматривать всю систему в целом, то она пять раз статически неопределима, так как нижний контур рамы замкнутый и, следовательно, неопределим трижды.

Систему, освобожденную от лишних связей, можно представить состоящей из двух защемленных внизу стержней с горизонтальными консолями (рис. 4.12, б).

Выяснить степень статической неопределимости этой системы можно иначе. Верхний контур рамы, имеющий один внутренний шарнир, дважды статически неопределим (имеет две лишние связи). Кроме того, каждая из заделок дает три составляющие опорной реакции (две силы и момент), т. е. на раму наложено шесть внешних связей, а уравнений статики для плоской системы можно составить лишь три. Следовательно, три внешние связи являются лишними, а всего имеется пять лишних связей, т. е. система пять раз статически неопределима.

Необходимо заметить, что исключение лишних связей для превращения одной и той же статически неопределимой конструкции в статически определимую можно произвести различными способами, однако число отбрасываемых связей всегда одно и то же. Так, например, статически определимые системы, изображенные на рис. 1.12, б, в, получены из статически неопределимой системы (см. рис. 1.12, а); одна — путем удаления промежуточной опоры, а другая — путем постановки промежуточного шарнира, т. е. удаления связи, препятствующей взаимному повороту частей балки, расположенных по обе стороны от введенного шарнира.

Включение шарнира в узел рамы, в котором сходятся два стержня, или же установка его в любое место на оси стержня нарушает (снимает) одну связь и снижает общую степень статической неопределимости системы на единицу. Такой шарнир будем называть одиночным, или простым.

При удалении связей системы необходимо следить за тем, чтобы получаемая конструкция была геометрически неизменяема. Поэтому в раме, показанной на рис. 5.12, а, имеющей одно лишнее опорное закрепление, было бы ошибочным удаление вертикального стерженька (рис. 5.12, б), так как оставшиеся три стерженька не могли бы препятствовать повороту рамы вокруг точки , в которой пересекаются их оси.

Правильный вариант удаления лишнего стержня показан на рис. 5.12, б.

Для конструкций со сложным внутренним образованием можно применить следующий общий прием определения степени статической неопределимости. Идея его заключается в том, что каждый шарнир, включенный в узел, соединяющий k стержней, снижает степень статической неопределимости на так как такой шарнир заменяет одиночных шарниров (рис. 6.12, а). Поэтому для определения степени статической неопределимости конструкции необходимо взять утроенное количество замкнутых контуров (предполагая, что все шарниры, в том числе и опорные, заменены жесткими соединениями) и затем уменьшить его на число включенных в конструкцию одиночных шарниров, учитывая при этом, что один общий шарнир эквивалентен одиночным шарнирам.

Представим это в виде формулы

где — степень статической неопределимости системы; — число замкнутых контуров в конструкции в предположении отсутствия шарнирных соединений; — число одиночных шарниров; шарнир, соединяющий два стержня, считается за один (одиночный шарнир), соединяющий три стержня — за два одиночных шарнира (двойной шарнир) и т. д.

Рассмотрим теперь раму, изображенную на рис. 7.12, а. Эту раму можно представлять как один замкнутый контур с введен ными в него двумя одиночными шарнирами (рис. 7.12, б). Степень ее статической неопределимости на основании формулы (1.12) равна единице:

Раму, изображенную на рис. 7.12, в, можно рассматривать как состоящую из двух замкнутых контуров с введенными в нее пятью одиночными шарнирами (рис. 7.12, г). Следовательно, степень статической неопределимости этой рамы равна единице:

Систему, изображенную на рис. 7.12, д, можно рассматривать как три замкнутых контура, в которые введены три одиночных и один двойной шарнир (посередине правой стойки).

Следовательно, эта система четырежды статически неопределима:

Если в статически определимой системе устранить какую-либо связь, то система, как отмечалось, превратится в геометрически изменяемую. Следовательно, статически определимая система содержит в своем составе такое количество связей, которое является минимально необходимым для обеспечения ее геометрической неизменяемости; избыточные связи (сверх этого количества) создают статическую неопределимость.

Из любой статически неопределимой системы можно устранить по крайней мере одну связь без нарушения ее изменяемости; однако удаление некоторых связей может превратить статически неопределимую систему в геометрически изменяемую. Такие связи статически неопределимой системы являются абсолютно необходимыми. Усилия в них всегда можно определить при помощи одних лишь уравнении статики.

Примером абсолютно необходимых связей являются вертикальные опорные стержни рамы, показанной на рис. 5.12, а; удаление одного из них делает раму геометрически изменяемой.

Связи, удаление которых не превращает статически неопределимую систему в геометрически изменяемую, называются условно необходимыми. Усилия в них нельзя определить при помощи одних лишь уравнений статики. Примером таких связей являются горизонтальные опорные стержни рамы, изображенной на рис. 5.12, а.

Источник

iSopromat.ru

Статически неопределимыми называют балки, для которых при определении опорных реакций и внутренних силовых факторов недостаточно одних только уравнений равновесия.

Другими словами, СН балки имеют «лишние» опоры, которые дают дополнительные связи, сверх необходимых для удержания системы в равновесии.

Для раскрытия статической неопределимости таких балок требуются дополнительные уравнения, получаемые из условия отсутствия или совместности перемещений некоторых сечений.

Примеры статически неопределимых балок

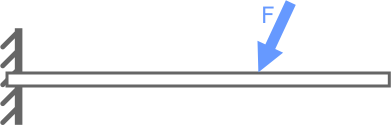
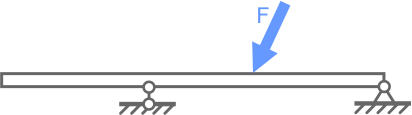
Для удержания балки в геометрически неизменяемом, статичном положении (в равновесии) требуется одна заделка (рис. 1 а) либо две шарнирные опоры (рис. 1 б) одна из которых подвижная другая неподвижная.

Добавление еще одной опоры (Рис. 2) упрочнит балку, но при этом она станет статически неопределимой.

Усилия в дополнительных опорах являются лишними неизвестными при решении систем уравнений статики.

Степень статической неопределимости балки

Количество дополнительных связей показывает степень статической неопределимости балки, которую можно определить по формуле:

где m – общее количество неизвестных реакций связи балки,
n – количество возможных уравнений равновесия которые можно составить для данной системы (для плоской – 3, пространственной – 6).

Балки с одной дополнительной связью называют однажды (один раз) неопределимыми, с двумя – дважды неопределимыми и т.д.

Раскрытие статической неопределимости

Расчет величины и направления лишних связей называют раскрытием статической неопределимости.

Так как для статически неопределимых балок возможных уравнений равновесия всегда меньше чем неизвестных усилий для их расчета требуются дополнительные зависимости.

В качестве таковых используются условия отсутствия соответствующих линейных и/или угловых перемещений на опорах.

Существуют теоретические и практические методы раскрытия статической неопределимости.

Раскрыть статическую неопределимость балки можно с помощью метода начальных параметров или методом сил.

Практический метод определения лишней опорной реакции подробно рассмотрен здесь.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник