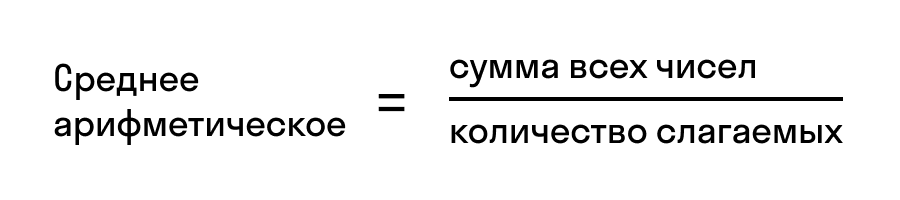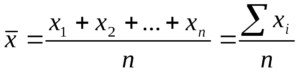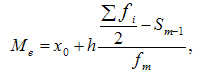Что называется средним арифметическим ряда чисел может ли среднее арифметическое ряда чисел
Что называется средним арифметическим ряда чисел может ли среднее арифметическое ряда чисел
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Для ряда a1,a1. an среднее арифметическое вычисляется по формуле:
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.
3 простых формулы, чтобы посчитать среднее арифметическое
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Вот так:
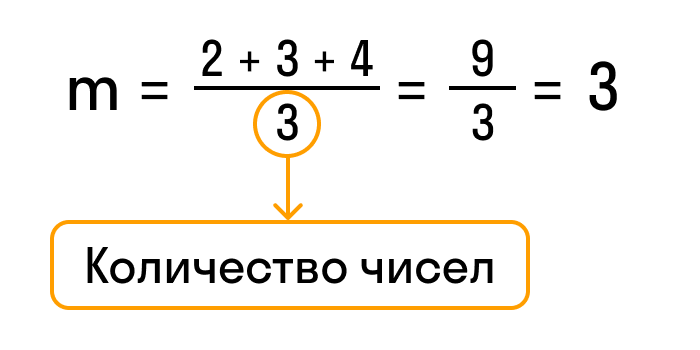
Например, найдем среднее арифметическое чисел 5, 6 и 7. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на три.
Так получилась формула среднего арифметического:
Способы вычисления среднего арифметического
Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:
Вычисление моды или наиболее часто встречающегося значения. Формула такая:
Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Что называется средним арифметическим ряда чисел может ли среднее арифметическое ряда чисел
Среднее арифметическое ряда чисел – это сумма данных чисел, поделенная на количество слагаемых.
Среднее арифметическое называют средним значением числового ряда.
Пример : Найдем среднее арифметическое чисел 2, 6, 9, 15.
Решение. У нас четыре числа. Значит, надо их сумму разделить на 4. Это и будет среднее арифметическое данных чисел:
(2 + 6 + 9 + 15) : 4 = 8.
Среднее геометрическое ряда чисел – это корень n-й степени из произведения этих чисел.
Пример : Найдем среднее геометрическое чисел 2, 4, 8.
Решение. У нас три числа. Значит, надо найти корень третьей степени из их произведения. Это и будет среднее геометрическое данных чисел:
3 √ 2 · 4 · 8 = 3 √64 = 4
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Пример : Найти размах чисел 2, 5, 8, 12, 33.
Решение : Наибольшее число здесь 33, наименьшее 2. Значит, размах составляет 31:
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Пример : Найти моду ряда чисел 1, 7, 3, 8, 7, 12, 22, 7, 11, 22, 8.
Решение : Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медиана.
В упорядоченном ряде чисел:
Медиана нечетного количества чисел – это число, записанное посередине.
Пример : В ряде чисел 2, 5, 9, 15, 21 медианой является число 9, находящееся посередине.
Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Пример : Найти медиану чисел 4, 5, 7, 11, 13, 19.
Решение : Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел:
Число 9 и является медианой данного ряда чисел.
В неупорядоченном ряде чисел:
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Пример 1 : Найдем медиану произвольного ряда чисел 5, 1, 3, 25, 19, 17, 21.
Решение : Располагаем числа в порядке возрастания:
1, 3, 5, 17, 19, 21, 25.
Посередине оказывается число 17. Оно и является медианой данного ряда чисел.
Пример 2 : Добавим к нашему произвольному ряду чисел еще одно число, чтобы ряд стал четным, и найдем медиану:
5, 1, 3, 25, 19, 17, 21, 19.
Решение : Снова выстраиваем упорядоченный ряд:
1, 3, 5, 17, 19, 19, 21, 25.
Посередине оказались числа 17 и 19. Находим их среднее значение:
Число 18 и является медианой данного ряда чисел.
Разработка серии уроков по алгебре для 7-го класса по теме «Статистические характеристики»
Разделы: Математика
Урок 1. «Среднее арифметическое, размах и мода»
Тип урока: ознакомление с новым материалом.
Цели:
Оборудование: проектор.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
Слышали ли вы когда-нибудь такую песню: «Потому что на десять девчонок по статистике девять ребят»? Как вы думаете, что это значит?
Сегодня мы познакомимся с новой наукой – статистикой. Узнаем, что она изучает и как можно применить те знания, которые вы сейчас получите.
III. Актуализация знаний
– Какое число называют средним арифметическим нескольких чисел?
(Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых).
Задача: дан ряд чисел 5, 6, 8, 12, 15, 4, 17, 8, 10, 15.
IV. Первичное усвоение, осознание и осмысление нового материала
– Ребята, вы начинаете изучать новый предмет: «Элементы статистики и теории вероятностей».
– Где в реальной повседневной жизни мы сталкиваемся с этими науками?
– Вы что-нибудь слышали об этом разделе математики?
– А разве вам не приходилось подсчитывать среднюю скорость движения, средний бал ученика, класса. Подготовку человека к таким проблемам во всем мире осуществляет школьный курс математики, и в частности ее раздел «Математическая статистика».
Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов. Вам было дано задание: измерить время, затраченное на выполнение домашнего задания по алгебре.
Мы получили следующие результаты: 27, 25, 26, 25, 40, 38, 38, 25 и т.д.
Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания.
– Что для этого нужно сделать? (сложить все числа и разделить полученную сумму на их количество).
Число 28, полученное в результате, называют средним арифметическим рассматриваемого ряда. Обозначение: 
.
Мы вычислили, что на выполнение домашнего задания по алгебре учащиеся затратили в среднем 28 минут. Проводя аналогичные наблюдения, можно проследить, какова была средняя затрата времени на выполнение в какой-либо день домашнего задания по алгебре и русскому языку.
Заметим, что иногда вычисление среднего арифметического не дает полезной информации, так как время, затраченное некоторыми учащимися, значительно отличается от среднего арифметического.
Наибольший расход времени равен 40 минут, а наименьший расход времени равен 18 минут. Разность между наибольшим и наименьшим значением называется размахом ряда.
Размах ряда находят тогда, когда хотят определить, как велик разброс данных в ряду.
-Ребята, нас могут интересовать не только среднее арифметическое и размах, но и другие показатели.
Например, интересно знать, какое число встречается в ряду данных чаще всего.
Таким числом является число 25. Число, наиболее часто встречающееся в данном ряду, называется модой чисел.
Ряд может иметь две моды, а может не иметь моды. Например, 47, 46, 50, 52, 47, 49, 52, 55 – имеет две моды: 47 и 52.
69, 68, 66, 70, 67, 71, 74, 63, 73, 72 – этот ряд не имеет моды.
– Ребята, где еще можно встретить понятие моды ряда чисел?
– Данные о размерах мужских сорочек, проданных в определенный день в универмаге. Здесь мода – размер пользующихся спросом, мода – цены на товар распространенный на рынке и т.п.
V. Закрепление изученного материала
При выставлении оценок учитель также вычисляет среднее арифметическое ваших текущих оценок.
Сейчас вы получите выписку ваших оценок по алгебре за I четверть.
Вы должны вычислить среднее арифметическое, моду и размах.
VI. Подведение итогов урока
Выставление оценок за работу на уроке.
«В среднем в день ребёнок улыбается 400 раз, взрослый — 17. Теперь все улыбнулись, чтобы испортить статистику»
VIII. Рефлексия
Раздать карточки для рефлексии.
VII. Постановка домашнего задания п. 9, 168 (а, б), 172, 178
Урок 2. «Медиана как статистическая характеристика»
Тип урока: ознакомление с новым материалом.
Цели:
Оборудование: проектор
Ход урока
I. Организационный момент
II. Проверка домашнего задания
III. Сообщение темы и целей урока
Сегодня на уроке мы повторим алгоритм нахождения среднего арифметического, размаха и моды, и узнаем, как находится еще одна характеристика – медиана.
IV. Актуализация опорных знаний учащихся
1. Фронтальный опрос.
а) Дан ряд чисел: 3, 5, 1, 7, 9. Найти среднее арифметическое, размах и моду.
б) Дан ряд чисел: 1, 2, 2, 5, 5. Найти среднее арифметическое, размах и моду.
V. Первичное усвоение, осознание и осмысление нового материала
Задача. В небольшой фирме 10 сотрудников: 7 рабочих, мастер, бухгалтер, директор. Зарплата у рабочих: 2000, у мастера 4000, у бухгалтера 16000, у директора 40000. Найдите чему будет равна средняя зарплата на этом предприятии?
Но достаточно ли этой характеристики работнику, который устраивается работать рабочим? (Нет)
В этом случае используют другую статистическую характеристику – медиану.
Запишем алгоритм нахождения медианы набора чисел:
Медиану используют вместо средней арифметической, когда крайние варианты упорядоченного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.
VI. Закрепление изученного материала
Задача 2. В таблице приведена информация о длине основных рек, протекающих по территории округа Домодедово Московской области.
| Река | Длина, км |
| Пахра | 900 |
| Рожайка | 51 |
| Битца | 24 |
| Гнилуша | 31 |
| Северка | 98 |
| Конопелька | 13 |
а) Найдите среднюю длину рек (среднее арифметическое);
б) Найдите длину рек в среднем (медиану данных);
в) По вашему мнению, какая из этих характеристик – среднее арифметическое или медиана – лучше описывает длину рек, протекающих в Домодедовском районе? Ответ объясните.
Ответ: а) 186 км, б) 41 км, в) медиана, т.к. данные содержат значения сильно отличающиеся от всех прочих.
Итак, для характеристики статистической информации используют среднее арифметическое и медиану. Во многих случаях одна из характеристик может не иметь никакого содержательного смысла.
VI. Подведение итогов урока
У статистиков есть шутка: средняя глубина озера 0,5 м, а корова все-таки утонула. Как вы понимаете эту фразу?
Выставление оценок за работу на уроке.
VIII. Рефлексия
Раздать карточки для рефлексии.
VII. Постановка домашнего задания п.10, 187, 190, 193
Урок 3. «Статистические характеристики»
Тип урока: закрепление изученного.
Цели:
Оборудование: карточки для выполнения проверочной работы.
Ход урока
I. Организационный момент
II. Проверка домашнего задания, уточнение направлений актуализации материала
III. Сообщение темы, цели и задач урока, мотивация учения
Сегодня на уроке мы продолжим находить основные статистические характеристики числовых рядов.
IV. Воспроизведение изученного и их первичное применение в новых или измененных условиях с целью формирования умений
1. Фронтальный опрос
В таблице приведены расходы учащегося 7 класса за 4 дня:
| День | Понедельник | Вторник | Среда | Четверг |
| Расходы | 100 | 75 | 50 | 75 |
Определить какая статистическая характеристика находится в каждом задании:
б) 50, 75, 75, 100;
(75+75):2 = 75;
___=75 р.
в) 100, 75, 50, 75;
___=75 р.
3. Решение заданий повышенной сложности
V. Проверочная работа
Выдаются карточки с заданием. Эти карточки подписываются учащимися. Задания выполняются на этих карточках в течение 3-5 минут.
Ребята меняются карточками. И по готовым ответам на доске проверяют работы друг друга и выставляют отметки согласно предложенным критериям.
Оценка: «5» – всё верно; «4» – 3 задания выполнены верно; «3» – 2 задания выполнены верно; «2» – выполнено верно менее двух зданий.
Работы сдаются учителю для просмотра и анализа усвоения материала.
VI. Подведение итогов урока
Выставление оценок за урок.
VII. Рефлексия
Раздать карточки для рефлексии.
VIII. Постановка домашнего задания №182, №183, №193
Провести сбор информации на тему: «Размер обуви учеников 7 класса», «Рост учеников 7 класса», «Количество детей в семье учеников 7 класса» (в трех экземплярах)
Урок 4. «Статистические характеристики нашего класса»
Тип урока: обобщения и систематизации знаний.
Цели:
Оборудование: таблицы для заполнения данных.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
– На перемене я собрала ответы на все ваши вопросы. Все готовы приступить к групповому исследованию. Начинаем заключительный урок по теме “Статистические характеристики”.
III. Воспроизведение и коррекция опорных знаний
IV. Обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий
Сегодня на уроке мы проведем с вами статистическое исследование.
Запишем основные этапы статистического исследования:
Рассмотрим следующую задачу:
В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:
| Цена (руб.) | 500 | 1200 | 1500 | 1800 | 2000 | 2500 |
| Количество | 8 | 9 | 14 | 15 | 3 | 1 |
Первый и второй этап статистического исследования уже пройдены: данные собраны и систематизированы. Осталось произвести анализ данных.
Для данных показателей надо найти статистические характеристики и объяснить их значение. После ученики должны ответить на следующие вопросы:
По каким параметрам еще можно провести статистические исследования в обувном магазине?
V. Усвоение ведущих идей и основных теорий на основе широкой систематизации знаний
Проведем собственное статистическое исследование. У вас было домашнее задание: принести данные о своем росте, размере обуви и количестве детей в семье.
Сейчас каждый ряд получит свое задание :
Так как статистическое исследование состоит из трех этапов, а первый этап – сбор данных мы уже провели, то вы можете переходить ко второму этапу – систематизации данных. Для этого данные занесите в таблицы.
После того как вы провели систематизацию данных, можно переходить к следующему этапу – анализу данных. Найдите статистические характеристики: среднее арифметическую, моду, медиану и размах ряда. Сделайте выводы.
VI. Подведение итогов урока
Вы все отлично справились с заданием. Выставление оценок за работу на уроке.
VII. Постановка домашнего задания
Провести исследование на тему: «Рост учащихся 8 класса».
Что называется средним арифметическим ряда чисел может ли среднее арифметическое ряда чисел
В этом учебном году мы начали изучать два предмета: алгебру и геометрию. При изучении алгебры что-то мне знакомо из курса 5,6 классов, что-то мы изучаем более основательно и углубленно, многое узнаем нового. Вот новое для меня при изучении алгебры – это знакомство с некоторыми статистическими характеристиками: размах и мода. Со средним арифметическим мы встречались уже ранее. Еще интересным оказалось, что эти характеристики применяются не только на уроках математики, но и в жизни, на практике (в производстве, в сельском хозяйстве, в спорте и т.д.).
Когда мы в классе на уроке решали задачи к этому пункту, то возникла идея составить самим задачи и подготовить к ним презентации, то есть как бы начать создавать свой задачник. Каждый придумывает задачу, делает к ней презентацию, как бы каждый работает над своим мини-проектом, а на уроке все вместе решаем, обсуждаем. Если допущены ошибки, то их исправляем. А в конце провести публичную защиту этих мини-проектов.
Цель моей работы: изучение статистики.
Задачи: начать разработку задачника по статистике в виде компьютерных презентаций.
Предмет исследования: статистика.
Объект исследования: статистические характеристики (среднее арифметическое, размах, мода).
В ходе изучения раздела «Статистические характеристики» мы познакомились с такими понятиями: среднее арифметическое, размах, мода. Эти характеристики находят применение в статистике. Эта наука изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т.п.
“Статистика знает всё”, – утверждали Ильф и Петров в своем знаменитом романе “Двенадцать стульев” и продолжали: “Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин, станков, велосипедов, памятников, маяков и швейных машинок… Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц. ” Это ироническое описание дает довольно точное представление о статистике (от лат. status – состояние) – науке, изучающей, обрабатывающей и анализирующей количественные данные о самых разнообразных массовых явлениях в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления.
Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
А еще есть статистика финансовая, налоговая, биологическая, метеорологическая. [1]
В школьном курсе алгебры мы рассматриваем понятия и методы описательной статистики, которая занимается первичной обработкой информации и вычислением наиболее показательных числовых характеристик. По словам английского статистика Р. Фишера: “Статистика может быть охарактеризована как наука о сокращении и анализе материала, полученного в наблюдениях”. Всю совокупность числовых данных, полученных в выборке можно (условно) заменить несколькими числовыми параметрами, некоторые из них мы уже рассматривали на уроках – это среднее арифметическое, размах, мода. Результаты статистических исследований широко используются для практических и научных выводов, поэтому важно уметь определять эти статистические характеристики.
Результаты статистических исследований широко используются для практических и научных выводов. [2]
Определение 1. Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых. [3]
Пример: При изучении учебной нагрузки выделили группу из 12 учащихся 7 класса. Просили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25. Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания по алгебре. Для этого надо сложить указанные 12 чисел и полученную сумму разделить
Число 27, полученное в результате, называют средним арифметическим рассматриваемого ряда чисел.
Среднее арифметическое является важной характеристикой ряда чисел но иногда полезно рассматривать и другие средние.
Определение 2. Модой ряда чисел называется число, которое встречается в данном ряду чаще других. [4]
Пример: При анализе сведений о времени, затраченном учащимися на выполнение домашнего задания по алгебре, нас могут заинтересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Например, интересно знать, какой расход времени является типичным для выделенной группы учащихся, т.е. какое число встречается в ряду данных чаще всего. Нетрудно заметить, что в нашем примере это число 25. говорят, что число 25 – мода рассматриваемого ряда.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем. Например, в ряду чисел 47, 46, 50, 47, 52, 49, 45, 43, 54, 52, 47, 52 две моды – это числа 47 и 52, так как каждое из них встречается в ряду по три раза, а остальные числа – менее трех раз.
В ряду чисел 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72 моды нет.
Моду ряда данных обычно находят, когда хотят выявить некоторый типичный показатель. Мода—показатель, который широко используется в статистике. Одним из наиболее частых использований моды является изучение спроса. Например, при решении вопросов, в пачки какого веса фасовать масло, какие открывать авиарейсы и т. п., предварительно изучается спрос и выявляется мода — наиболее часто встречающийся заказ.
Однако нахождение среднего арифметического или моды далеко не всегда позволяет делать надежные выводы на основе статистических данных. если у нас есть ряд данных, то для обоснованных выводов и надежных прогнозов на их основе, помимо средних значений, надо еще указать, насколько используемые данные различаются между собой. Одним из статистических показателей различия или разброса данных является размах.
Определение 3. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. [5]
Пример: В рассмотренном выше примере мы нашли, что в среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27 минут. Однако анализ проведенного ряда данных показывает, что время, затраченное некоторыми учащимися, существенно отличается от 27 минут, т.е. от среднего арифметического. Наибольший расход равен 37 минут, а наименьший – 18 минут. Разность между наибольшим и наименьшим расходом времени составляет 19 минут. Вот в этом случае рассматривается еще одна статистическая характеристика – размах. Размах ряда находят, когда хотят определить, как велик разброс данных в ряду.
А теперь хочу представить результаты нашей работы: мини-проекты для создания задачника по статистике.
Задача № 1. Автор Кушнарев Павел, учащийся 7 класса.
Я работаю в салоне-магазине «Супер-авто» главным менеджером отдела продаж. Наш салон предоставлял автомобили для участия в игре «полный привод». В прошлом году на выставке-продаже наши машины имели успех! Результаты продаж следующие: