Что называется случайной составляющей погрешности
Характеристики случайной составляющей погрешности
Под случайной составляющей инструментальной погрешности 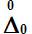
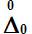
Характеристики случайной составляющей нормируются путем установления предела допускаемого среднеквадратичного отклонения.
Характеристика случайной составляющей погрешности от гистерезиса.
Эта характеристика называется вариацией выходного сигнала СИ. Она представляет собой основание закона распределения случайной составляющей погрешности от гистерезиса. Под случайной составляющей погрешности Δон понимается случайная составляющая погрешности СИ, обусловленная отличием показаний данного экземпляра измерительного прибора от информативного параметра входного сигнала при различных скорости и направлении его изменения.
Характеристика случайной составляющей погрешности от гистерезиса нормируется путем установления предела Н OP допускаемой вариации выходного сигнала (показания) СИ.
Если известны нормированные значения характеристик составляющих инструментальной погрешности М[ΔOS ], S[ΔOS], S [ 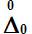
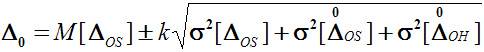
Эта группа описывает дополнительную погрешность или разность между значением погрешности, соответствующей некоторому значению влияющей величины в пределах рабочих условий применения СИ, и значением погрешности, соответствующим нормальному значению влияющей величины.
Динамические характеристики СИ.
Метрологические характеристики влияния на инструментальную составляющую погрешности измерения
К указанным характеристикам относятся характеристики СИ, отражающие их способность влиять на инструментальную составляющую вследствие взаимодействия СИ с любым из подключенных к его входу или выходу компонентов, например объектом измерений и др. Потребление энергии средством измерений от объекта измерения или от предвключенного прибора приводит к изменению значения измеряемой величины и, следовательно, к появлению соответствующей составляющей погрешности. Например, на погрешность измерения температуры с помощью термопар и термометров существенно влияет обмен тепловой энергией между объектом и прибором. Следовательно, для СИ, работа которых характеризуется обменом энергией между ними и подключенными к их входу или выходу объектами, необходимо нормировать некоторые характеристики, описывающие свойства этих приборов отбирать или отдавать энергию через свои входные или выходные цепи. Такие характеристики часто называют импедансными, или просто импедансами.
Вопросы нормирования импедансов средства измерений электрических величин разработаны достаточно полно. Сложнее обстоит дело с приборами для измерений неэлектрических величин, где явления обмена энергией, входные и выходные импедансы изучены недостаточно. В этом случае нормирование требует тщательных исследований.
Рассматриваемые характеристики нормируются путем установления номинальных значений импедансных характеристик и пределов допускаемых отклонений от них.
Неинформативные параметры выходного и входного сигналов СИ
Это такие параметры, которые не используются для передачи информации, но оказывают влияние на погрешность или результат измерения. Например, частота переменного тока при измерении его напряжения.
Кроме этих метрологических характеристик наиболее часто используются следующие технические характеристики СИ.
Разность между наибольшим и наименьшим значениями измерительного усилия при однонаправленном измерении значений измеряемой величины называется колебанием измерительного усилия.
Изменение измерительного усилия в момент перемены направления изменения значений измеряемой величины называется перепадом измерительного усилия.
Порог чувствительности прибора является решающим фактором при выборе измерительных средств для непрерывных измерений малых значений проверяемых величин (например, при проверке биения).
Согласно этому стандарту основная погрешность СИ не должна превышать одного из перечисленных ниже пределов:
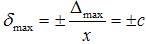
4. Если погрешность имеет как аддитивную, так и мультипликативную составляющие, то предел допускаемой относительной погрешности не должен превышать(в процентах)
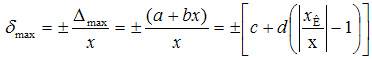
где a, b, c, d – постояные; xк – конечное значение диапазона измерения.
5. Приведенная погрешность не должна превышать
gmax = ±Dmax/x н= ± с (3)
При нормировании погрешности СИ постоянные a,b,c,d выбираются из следующего ряда предпочтительных чисел:
Числа 1, 6 и 3допускаются к применению, но не рекомендуются. Значение n принимается равным: +1,0, –1, –2 и т. д. Причем при одном значении n допускается устанавливать не более пяти различных пределов допускаемой погрешности для измерительных устройств конкретного вида.
В обоснованных случаях пределы допускаемой относительной погрешности определяются по другим формулам, на основании графика или таблицы.
Пределы допускаемых дополнительных погрешностей (ПДДП) устанавливают:
в виде постоянного значения для всей рабочей области влияющей величины или ее интервала;
отношения ПДДП, соответствующей интервалу величины, к этому интервалу;
зависимости ПДДП от номинальной или предельной функции влияния.
Как правило, ПДДП определяются в виде дольного значения предела допускаемой основной погрешности.
Классы точности определяются стандартами и техническими условиями, содержащими технические требования к СИ. Для каждого класса точности СИ конкретного типа устанавливаются конкретные требования к метрологическим характеристикам, в совокупности отражающие уровень точности. СИ нескольких физических величин или с несколькими диапазонами измерений могут иметь несколько классов точности. Классы точности присваивают при разработке СИ. В процессе эксплуатации метрологические характеристики СИ ухудшаются. Поэтому допускается понижение класса точности по результатам метрологической аттестации или поверки. Например, предусмотрено понижение класса точности при поверках концевых мер, если отклонение длины меры от номинального значения превышает предел допускаемых отклонений для класса точности, присвоенного ранее.
Обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений, приводятся в нормативно-технических документах. При этом в эксплуатационной документации на средство измерений, содержащей обозначение класса точности, должна быть ссылка на стандарт или технические условия, в которых установлен класс точности для этого типа средств измерений.
Обозначения могут иметь форму заглавных букв латинского алфавита (например, М, С и т. д.) или римских цифр (I, II, III, IV и т. д.) с добавлением условных знаков. Смысл таких обозначений раскрывается в нормативно-технической документации.
Для СИ, пределы допускаемой основной погрешности которых выражены в форме приведенной или относительной погрешности в соответствии с выражениями (1) и (3), классы точности обозначаются числами, равными этим пределам в процентах. Чтобы отличить относительную погрешность от приведенной, на СИ ее обводят кружком. С такой же целью под обозначением класса точности на СИ ставят знак “V”. Это означает, что предел абсолютной погрешности приведен к длине шкалы или к ее части, а не к номинальной точке шкалы.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Погрешность измерений. Классификация
Погрешность средств измерения и результатов измерения.
Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.
Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.
Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.
Статическая и динамическая погрешности.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Систематическая и случайная погрешности.
Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.
Причинами возникновения систематических составляющих погрешности измерения являются:
Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.
Погрешности адекватности и градуировки.
Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.
Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.
Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.
Абсолютная, относительная и приведенная погрешности.
Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.
Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.
Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.
Аддитивные и мультипликативные погрешности.
Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.
Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:
– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).
Что называется случайной составляющей погрешности
Всероссийский научно-исследовательский институт
оптико-физических измерений

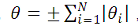






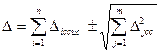 ,
,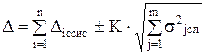 ,
,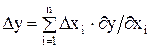 , (5)
, (5)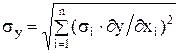 . (6)
. (6)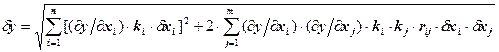 ,
,