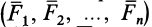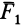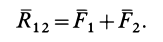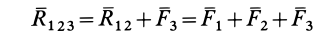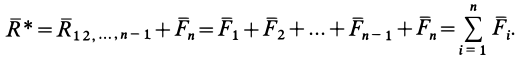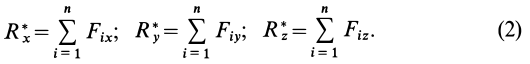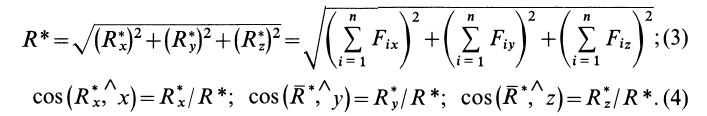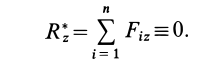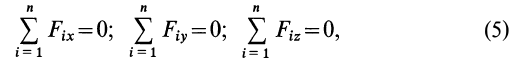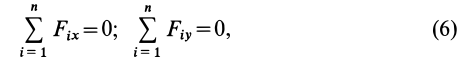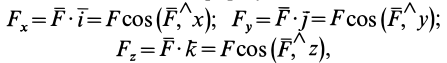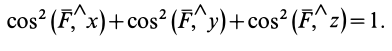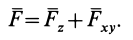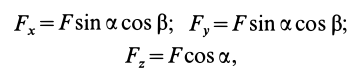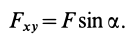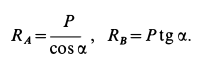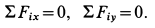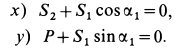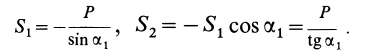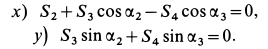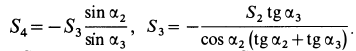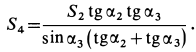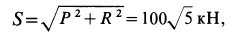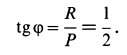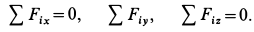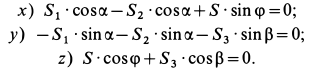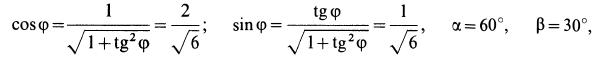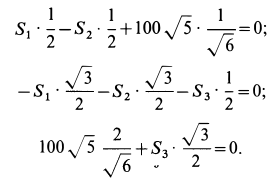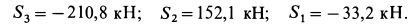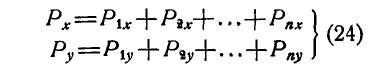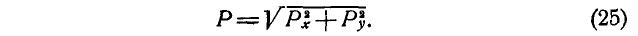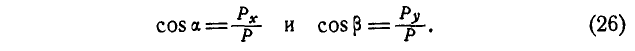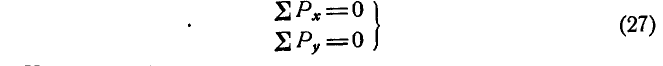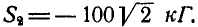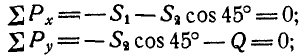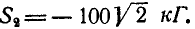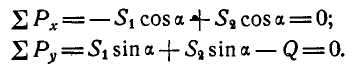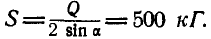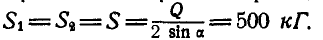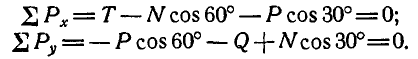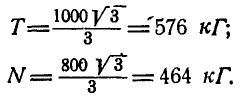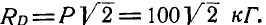Что называется сходящимися силами
Система сходящихся сил в теоретической механике
Содержание:
Система сходящихся сил:
Рассмотрим одну из важных систем сил — систему сходящихся сил. Для этой системы сил следует рассмотреть приведение ее к простейшему виду и установить условия равновесия.
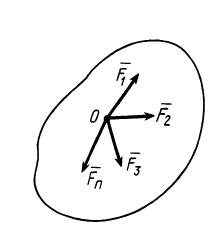
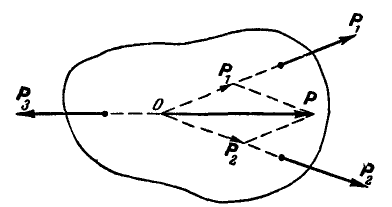
Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке — центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими, т. е. расположенными в одной плоскости.
Приведение к равнодействующей силе
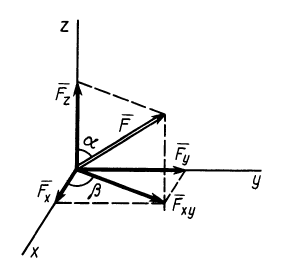
Рассмотрим общий случай пространственной системы сходящихся сил. Так как сила, действующая на твердое тело, есть вектор скользящий, то можно считать, что силы системы
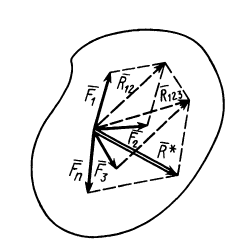
Применяя к первым двум силам пучка
Затем по правилу параллелограмма складываем силы 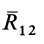
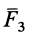
Рис. 12
Рис. 13
и т. д. Продолжая процесс векторного сложения сил для всех 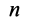
Таким образом, система 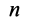
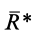
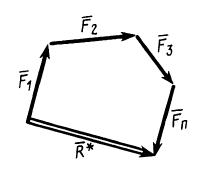
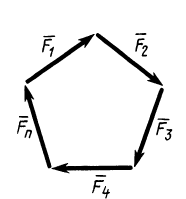
Процесс последовательного применения к силам правила параллелограмма, или их векторного сложения, приводит к построению силового многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой (рис. 14). Равнодействующая сила 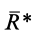
Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской— плоской. Для плоской системы сходящихся сил равнодействующую силу можно определить графически путем построения замыкающей силового многоугольника в выбранном для сил масштабе. Для пространственной системы сходящихся сил пришлось бы силовой многоугольник строить в пространстве из стержней.
Рис. 14
Итак, система сходящихся сил в общем случае приводится к одной силе—равнодействующей этой системы сил, которая изображается замыкающей силового многоугольника, построенного на силах системы. Линия действия равнодействующей силы проходит через центр пучка параллельно замыкающей силового многоугольника.
Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться известной из геометрии теоремой о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраической сумме проекций составляющих его сторон на ту же ось.
Так как равнодействующая сила 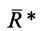
Проецируя векторы векторного равенства на прямоугольные оси координат, согласно теореме о проекции замыкающей получим
По проекциям определяем модуль равнодействующей силы и косинусы углов ее с осями координат по формулам
В формуле (3) перед квадратным корнем всегда берут знак плюс, так как определяется модуль равнодействующей силы.
В случае плоской системы сходящихся сил одну из координатных осей, обычно 
Условия равновесия системы сходящихся сил
Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпасть с началом первой силы. Такой силовой многоугольник называют замкнутым (рис. 15). Получено условие равновесия сходящихся сил в геометрической форме: для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.
Рис. 15
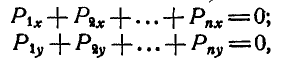
Для определения неизвестных сил при равновесии более предпочтительным является использование условий равновесия системы сходящихся сил в аналитической форме. Так как при равновесии системы сходящихся сил равнодействующая сила должна быть равна нулю (силовой многоугольник замкнут), то из этого следует, что равно нулю подкоренное выражение в (3), состоящее из суммы положительных величин. Таким образом, равны нулю квадраты каждой из величин подкоренного выражения, а следовательно, равны нулю и сами величины. Получаем условия равновесия пространственной системы сходящихся сил в аналитической форме:
т. е. для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю.
В случае плоской системы сходящихся сил одну из осей координат, обычно 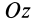
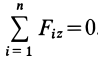
т. е. для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю.
Проецирование силы на оси координат
Если дана сила 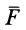
где 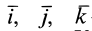
Из трех углов независимыми являются только два.
Рис. 16
При проецировании силы на прямоугольные оси координат целесообразно использовать тоже два угла. Для этого предварительно силу разлагают на две взаимно перпендикулярные составляющие, одна из которых параллельна какой-либо оси координат, например 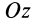
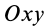
Проецируя векторы векторного равенства на координатные оси, имеем
При проецировании использованы только два угла: 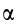
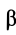
Векторные величины 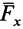
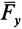
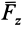
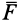
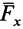
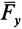
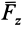
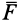
Пример 1.
Подъемный кран, имеющий вертикальную ось вращения 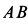
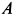
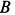
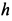
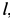
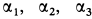
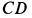
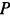
Решение. Считая кран твердым телом, освободим его от связей, которыми являются подпятник и подшипник, заменив их силами реакций связей. Сила реакции подшипника (цилиндрический шарнир) перпендикулярна его оси. Направление силы реакции подпятника заранее не известно и подлежит определению. На весь кран, находящийся в равновесии, действуют три силы: 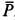
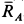
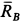
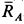
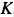
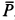
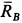
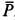
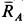
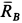
Рис. 17
Из геометрического треугольника
Для определения усилий в стержнях 1 и 2 применим метод вырезания узлов. Для этого рассмотрим равновесие отдельного шарнира или узла С. На этот узел действуют сила Р через трос и силы реакций стержней 1 и 2, которые следует мысленно отбросить. Силы реакций стержней на узел должны быть направлены по стержням, так как на эти стержни между их шарнирами другие силы не действуют. Стержни являются шарнирными. (Условимся силы реакций стержней направлять от узла (рис. 17, г) и знак вектора у сил на рисунке не ставить, чтобы не увеличивать без необходимости число обозначений для одинаковых по числовому значению сил.)
Выбрав в точке 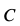

Эти условия в рассматриваемом случае принимают форму в проекциях на оси:
Из полученных уравнений получаем:
Знак 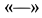
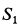

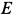

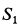
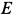

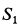
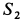
На узел 
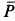
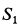
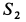
Из уравнений равновесия или силового треугольника можно определить только две неизвестные силы. Поэтому при дальнейшем решении задачи следует переходить к рассмотрению равновесия узла, на который действуют не более двух неизвестных сил. Таким узлом является узел 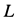
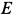
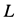
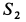
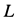
Из этих уравнений находим
Подставляя в выражение для 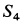
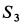
Усилие 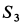
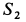
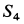
Для узла 
Пример 2.
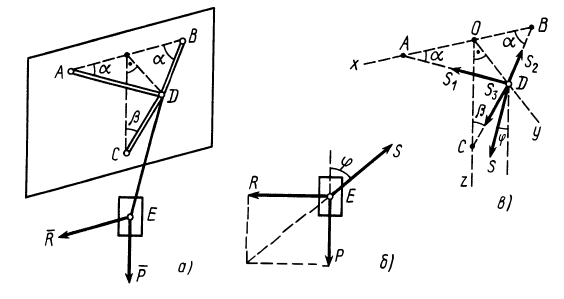
Груз с силой тяжести 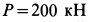
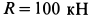
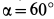
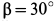
Решение. На находящийся в равновесии груз 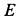
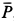
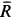
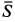
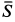
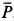
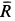
так как силы 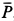
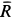
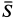
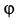
Рассмотрим равновесие шарнира 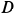
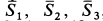
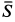
В рассматриваемом случае для выбранных осей координат имеем:
Рис. 18
то система уравнений принимает форму
Решая эту систему уравнений, получаем:
Усилия в стержнях направляли от рассматриваемого узла и получили 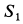
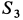
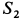
Силы, сходящиеся в одной точке
Если на точку А действуют n сил, расположенных в одной плоскости (рис. 22), то эти силы можно сложить геометрически, построив многоугольник векторов, который в нашем случае называется многоугольником сил.
Обозначая равнодействующую сил через Р, можем написать:
Проектируя равнодействующую и составляющие на координатные оси, проведенные через точку А, по формуле (3) имеем:
Величину равнодействующей находим по формуле (7):
Направление равнодействующей определяем по формулам (6):
Может оказаться, что при построении многоугольника сил конец последней силы совпадет с началом первой; в этом случае многоугольник сил получается замкнутым, равнодействующая сила равна нулю и силы находятся в равновесии. Таким образом, геометрическое условие равновесия сил, приложенных к точке, заключается в том, что многоугольник этих сил должен быть замкнут.
В этом случае Р=0, а поэтому и 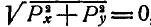
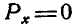
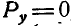
Уравнения (27) называются уравнениями равновесия сил, приложенных к точке, и выражают аналитические условия равновесия этих сил.
Рассмотрим равновесие трех сил 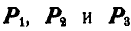
Пусть в точке О пересекаются линии действия любых двух сил, например 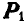
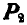
Теперь на тело уже действуют две силы Р и А, равновесие которых по аксиоме 2 возможно, если они будут направлены по одной прямой.
Отсюда заключаем, что три силы, действующие на тело, и расположенные в одной плоскости, могут находиться в равновесии только тогда, когда их линии действия пересекаются в одной точке.
Задача 1.
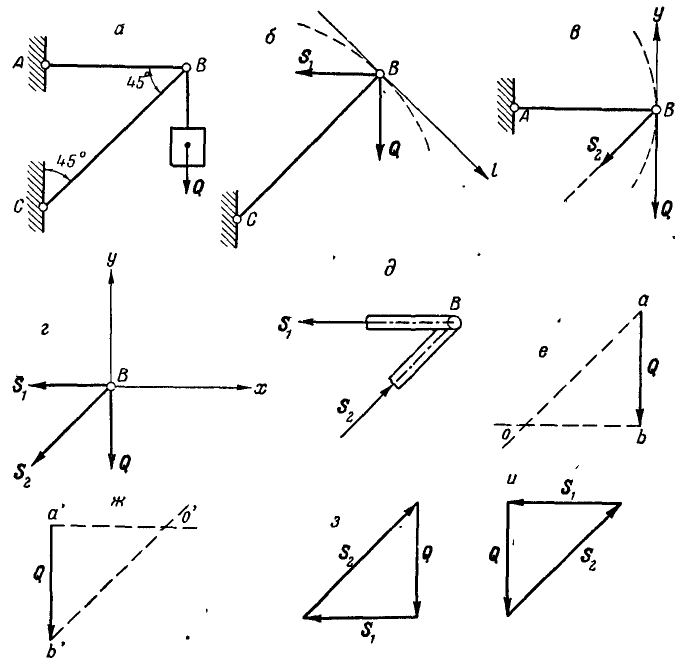
К точке В шарнирного кронштейна АВС (рис. 24, а) подвешен груз Q = 100 кГ. Определить усилия 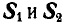
Решение. Для определения усилия 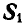
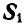
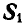
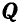
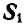
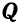
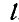
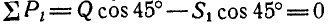
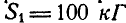
Для нахождения усилия 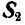
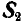
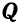
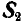
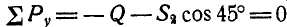
При решении этой задачи можно было бы освободиться одновременно от обеих связей ВА и ВС, вводя взамен их реакции связей 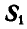
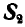
Тогда для свободной точки В можно написать два уравнения равновесия (27) в виде:
отсюда находим, что 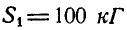
Знак минус у 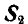
При неподвижной точке В реакция направленная от узла, будет растягивать стержень, а реакция 58, направленная к узлу, будет сжимать стержень, что ясно видно из чертежа.
Решим теперь эту задачу геометрическим способом. Все силы, заданные и реактивные, действующие на точку В, взаимно уравновешиваются, а поэтому многоугольник этих сил должен быть замкнут. На этом основании проводим вектор, равный силе 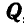
Выбрав один из полученных треугольников сил, замечаем, что сила 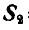
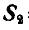
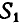
При решении дальнейших задач аналитическим способом стрелки неизвестных реакций стержней будём направлять всегда от рассматриваемого нами узла; тогда знак минус у модуля реакции какого-либо стержня будет указывать на то, что рассматриваемый нами стержень сжат.
Задача 2.
Определить усилия в стержнях АВ и ВС при действии в шарнире В силы Q=100 кГ, если АВ = ВС =5 м, BD = 0,5 м и шарниры А и С расположены на одной горизонтали (рис. 25, а).
Решение. Решим сначала задачу аналитическим способом, для чего рассмотрим равновесие точки В, находящейся под действием трех сил: заданной силы 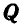
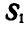
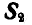
Применяя уравнения равновесия (27), имеем:
Из первого уравнения находим: 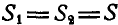
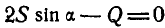
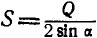
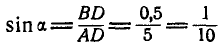
Знак плюс у S указывает на то, что оба стержня ВА и ВС растянуты.
Для решения этой задачи геометрическим способом, построим треугольник равновесия 0ab (рис. 25,в), из которого сразу находим правильное направление реакции 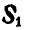
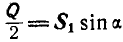
Задача 3.
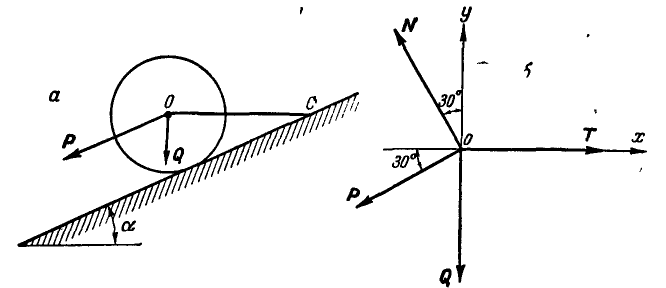
Однородный цилиндр (рис. 26,а) весом 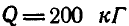
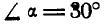
Решение. Решим задачу аналитическим способом. Освободившись от связей (рис. 26,6) и составляя для точки О уравнения равновесия (27), имеем:
Подставляя вместо Р и Q их значения и решая полученные уравнения, находим неизвестные силы:
Задача 4.
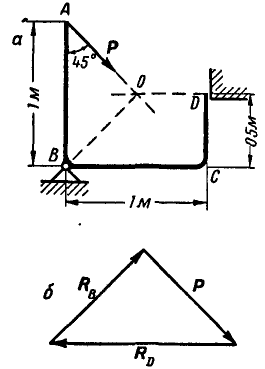
Жесткое колено ABCD (рис. 27,а), могущее вращаться вокруг шарнира В, опирается в точке D на гладкий уступ. Пренебрегая весом колена, определить реакции связей в точках В и D, если в точке А колена приложена сила Р=100 кГ.
Решение. Так как колено находится в равновесии, то три силы, действующие в точках А, В и D, должны пересекаться в одной точке. Продолжаем линию действия силы Р и реакции в точке D, направленной перпендикулярно к плоскости уступа, до взаимного пересечения в точке О; тогда линия действия реакции шарнира В пройдет обязательно через точку О. На рисунке 27, б дано построение треугольника равновесия трех сил 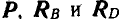
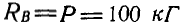
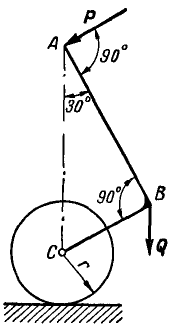
Задача 5.
При подъеме плуга на стоянке (рис. 30) поворачивают коленчатый рычаг АВС, вращая рукоятку силой Р. Какова при этом должна быть величина силы Р, если вес части плуга, передающейся на коленчатый рычаг, вращающийся вокруг шарнира В, равен Q = 30 кГ, длина рукоятки АВ = 0,6 м и радиус колеса плуга г = 0,25 м.
Решение. Строим для сил, приложенных к коленчатому рычагу, треугольник равновесия. Из подобия треугольника равновесия и соответствующего треугольника на чертеже находим силу Р.
Ответ: Р = 11 кГ.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.