Что называется произведением ненулевого вектора на число
Урок «Умножение вектора на число»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна модуль |k| умноженный на модуль |а|, причем векторы а и b сонаправлены, если k положительно и противоположно направлены, если k отрицательно.
Произведение вектора а на число k обозначается так: ka.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение любого вектора на число нуль есть нулевой вектор.
Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства:
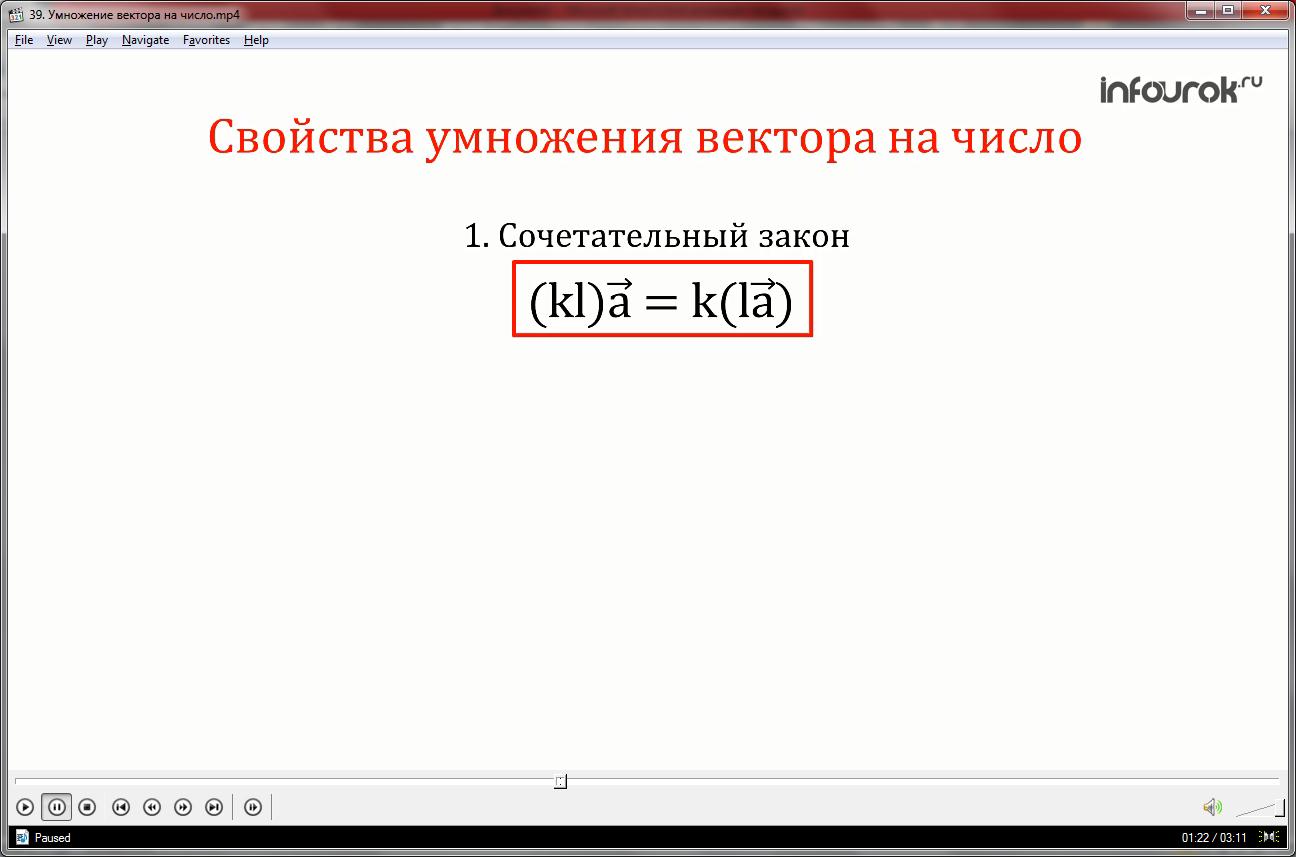
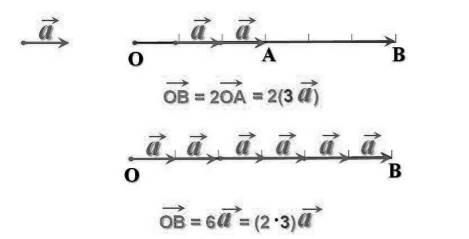
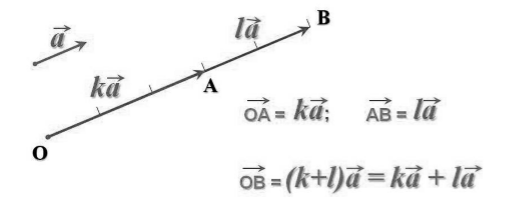
Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.
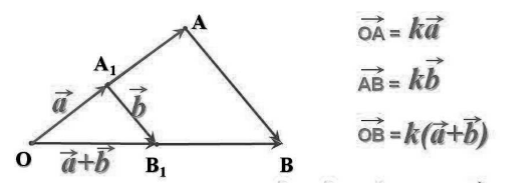
Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b.
На рисунке, на примере показано это свойство.
Третье свойство, второй распределительный закон. Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а.
На рисунке, на примере показано это свойство.
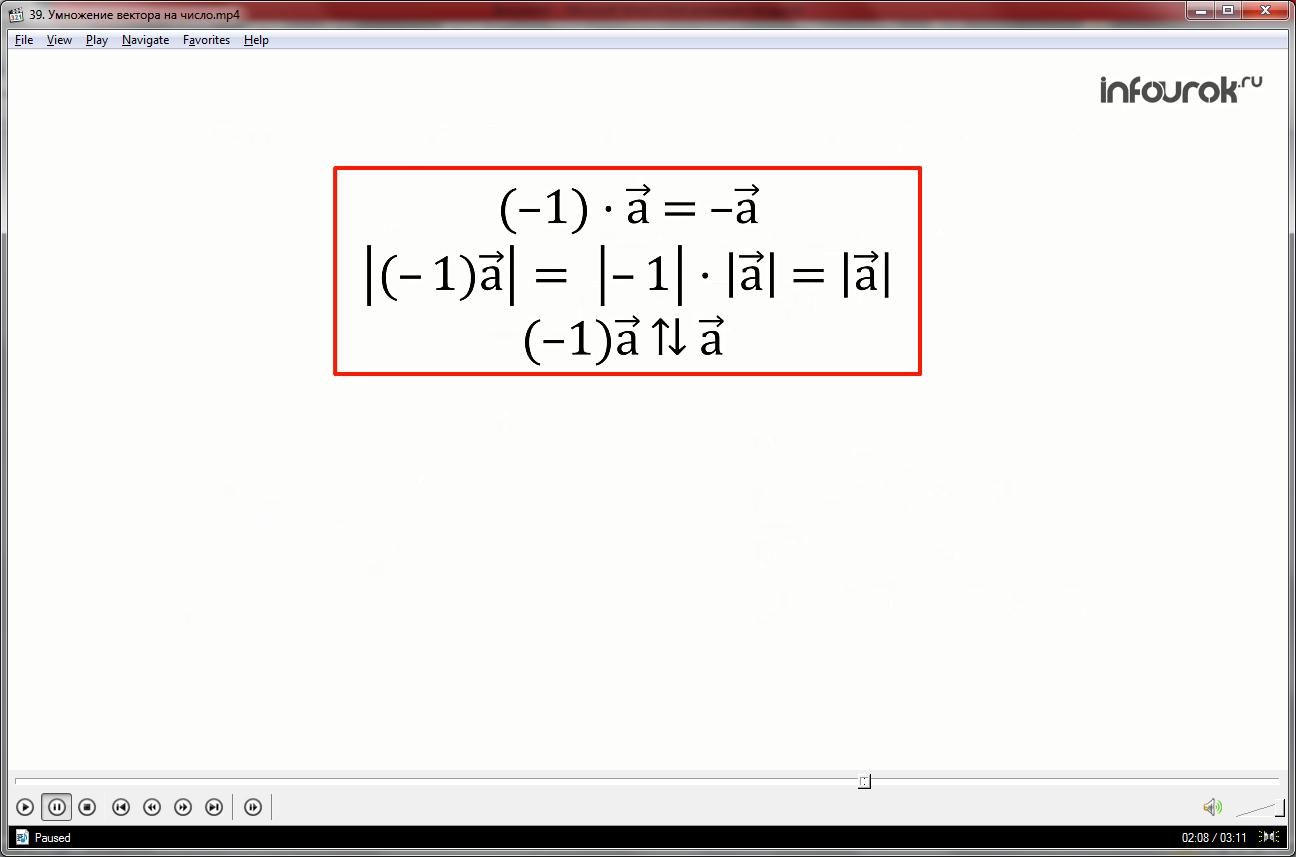
Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.
Для векторов в пространстве, как и в планиметрии, выполняется следующее условие:
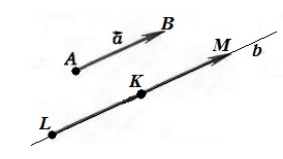
Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а.
Решим задачу №347 (а)
Необходимо упростить выражение.
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.
Презентация по геометрии на тему «Произведение вектора на число. Свойства произведения»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Произведение вектора на число. Свойства произведения 9 класс Л.С. Атанасян Учитель Коченко Светлана Викторовна
1) Постройте сумму а + b, используя правило треугольника. а b c Построение: d Дано: а b 1) a + b Повторение
5) Упростите выражение: 1 вариант. CA – OB – CD + AB = 2 вариант. BA + CD – OD – CA = = CA + BO + DC + AB = = DO. = BA + CD + DO + AC = = BA + AC + CD + DO = = BO. = DC + CA + AB + BO =
Рассмотрим пример: Один автомобиль движется прямолинейно с постоянной скоростью, второй автомобиль движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу и величина его скорости такая же, как у второго автомобиля. Изучение нового материала
Произведением ненулевого вектора a на число k называется такой вектор b, длина которого равна k a, причем векторы a и b сонаправлены при k0 и противоположно направлены при k0. Произведение нулевого вектора на любое число считается нулевой вектор 0 k =0 Произведение вектора a на число обозначается: k a. Определения:
Из определения произведения вектора на число следует, что: 1) произведение любого вектора на число нуль есть нулевой вектор a 0=0 ; 2) для любого числа k и любого вектора a векторы a и ka коллинеарные.
Основные свойства умножения вектора на число: Для любых чисел k, l и любых векторов a, b справедливы равенства: 1 2 3
Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2, l = 3. B O 1
2 Рисунок иллюстрирует первый распределительный закон. Представлен случай, когда k = 3, l = 2. B O OB =
Упражнение № 776 а) б)
Задача № 779 Решение. Аналогично получаем: а= а= р; р; Ответ: Направления: , , , , ; 2
Домашнее задание п. 83 № 776б, 780 Спасибо за внимание
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1400287
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Исследования вакцины для детей младше 12 лет начнутся с 2022 года
Время чтения: 1 минута
В России планируют создавать пространства для подростков
Время чтения: 2 минуты
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Более 50 российских школ перешли на дистанционку из-за коронавируса
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Лекция по математике на тему «Умножение вектора на число»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Лекция по теме «Умножение вектора на число»
Произведением ненулевого вектора а на число k называется такой вектор b , длина которого равна модуль | k | умноженный на модуль |а|, причем векторы а и b сонаправлены, если k положительно и противоположно направлены, если k отрицательно.
Произведение вектора а на число k обозначается так: ka .
Умножение вектора на число
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение любого вектора на число нуль есть нулевой вектор.
Умножение вектора на число


Рассмотрим основные свойства умножения вектора на число. Для любых векторов а, b и любых чисел k и l справедливы равенства:
Свойства умножения вектора на число
На рисунке, на примере показано это свойство.
Свойства умножения вектора на число
Первый распределительный закон
Третье свойство, второй распределительный закон. Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а.
На рисунке, на примере показано это свойство.
Свойства умножения вектора на число
Второй распределительный закон
Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.
(-1) 

Для векторов в пространстве, как и в планиметрии, выполняется следующее условие:
Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а.
Если 

Решим задачу №347 (а)
Необходимо упростить выражение.
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.


Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-025723
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
До конца 2024 года в РФ построят около 1 300 школ
Время чтения: 1 минута
Утверждено стратегическое направление цифровой трансформации образования
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Псковских школьников отправили на дистанционку до 10 декабря
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Основные свойства умножения вектора на число: описание, примеры
Содержание:
Изучающие математические науки и физику, начиная со старших классов, знакомятся с понятием «вектор». Это направленный отрезок, отличающийся от обычного (ненаправленного) рядом характеристик. Рассмотрим основные свойства умножения вектора на число. Ознакомимся с необходимыми для работы понятиями, приведём примеры задач.
Теория
Векторы применяются в геометрии, компьютерной графике, например, для создания карт освещения, прокладывания траекторий движения. Позволяют быстро вычислять площади геометрических фигур и объёмы тел. В физике векторами являются величины, имеющие направление: сила, ускорение. Обозначаются буквами с чёрточками, например, \overline, \overline, (\overline
Умножение вектора на число
При умножении пары чисел на вектор работают знакомые с начальных классов правила:
Особенности и закономерности произведения чисел и направленных отрезков:
Становится понятно, что произведением ненулевого вектора на число называется коллинеарный вектор. В геометрии:
В алгебре следствием произведения будет тот же вектор, сдвинутый в координатной сетке на указанное число в направлении, которое зависит от его знака.
Физический смысл преобразования – инверсия направления величины (действия силы) в зависимости от знака числа (если отрицательное, меняется на противоположное) с изменением её значения в n (модуль) раз.
Модули можно возводить в степень, перемножать между собой.
Умножение вектора на число
Вы будете перенаправлены на Автор24
Откладывание вектора от данной точки
Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Введем следующую теорему:
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Умножение вектора на число
Отметим, что в результате произведения вектора на число всегда получается векторная величина.
Свойства произведения вектора на число
Произведение любого вектора с числом ноль равняется нулевому вектору.
Доказательство.
Доказательство.
Доказательство этого закона иллюстрирует рисунок 3.
Рисунок 3. Сочетательный закон
Доказательство этого закона иллюстрирует рисунок 4.
Рисунок 4. Первый распределительный закон
Доказательство этого закона иллюстрирует рисунок 5.
Рисунок 5. Второй распределительный закон