Что называется произведением матриц

Умножение матриц: примеры, алгоритм действий, свойства произведения

Произведение двух матриц

Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:

C ⏟ m × n = A ⏟ m × p × B ⏟ p × n

Вычислим произведения АВ=ВА:

Решение, используя правило умножения матриц:

А ⏟ 2 × 3 × В ⏟ 3 × 2 = 1 2 1 0 1 2 × 1 0 0 1 1 1 = 1 × 1 + 2 × 0 + 1 × 1 1 × 0 + 2 × 1 + 1 × 1 0 × 1 + 1 × 0 + 2 × 1 0 × 0 + 1 × 1 + 2 × 1 = = 2 3 2 3 ⏟ 2 × 2

В ⏟ 3 × 2 × А ⏟ 2 × 3 = 1 0 0 1 1 1 × 1 2 1 0 1 2 = 1 × 1 + 0 × 0 1 × 2 + 0 × 1 1 × 1 + 0 × 2 0 × 1 + 1 × 0 0 × 2 + 1 × 1 0 × 1 + 1 × 2 1 × 1 + 1 × 0 1 × 2 + 1 × 1 1 × 1 + 1 × 2 = 1 2 1 0 1 2 1 3 3 ⏟ 3 × 3

Свойства умножения матриц

Свойства умножения матриц:

Проверяем свойство №1: ( А В ) С = А ( В С ) :

Проверяем свойство №2: А ( В + С ) = А В + А С :

Произведение трех матриц

Произведение трех матриц А В С вычисляют 2-мя способами:

Перемножить матрицы 2-мя способами:

Алгоритм действий:

Используем формулу А В С = ( А В ) С :

Умножение матрицы на число

Произведение матрицы А на число k — это матрица В = А k того же размера, которая получена из исходной умножением на заданное число всех ее элементов:

Свойства умножения матрицы на число:

Найдем произведение матрицы А = 4 2 9 0 на 5.

5 А = 5 4 2 9 0 5 × 4 5 × 2 5 × 9 5 × 0 = 20 10 45 0

Умножение матрицы на вектор

Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:

А В = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а m 1 а m 2 ⋯ а m n b 1 b 2 ⋯ b 1 n = a 11 × b 1 + a 12 × b 2 + ⋯ + a 1 n × b n a 21 × b 1 + a 22 × b 2 + ⋯ + a 2 n × b n ⋯ ⋯ ⋯ ⋯ a m 1 × b 1 + a m 2 × b 2 + ⋯ + a m n × b n = c 1 c 2 ⋯ c 1 m

А В = а а ⋯ а b b ⋯ b = a 1 × b 1 a 1 × b 2 ⋯ a 1 × b n a 2 × b 1 a 2 × b 2 ⋯ a 2 × b n ⋯ ⋯ ⋯ ⋯ a n × b 1 a n × b 2 ⋯ a n × b n = c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋯ ⋯ ⋯ ⋯ c n 1 c n 2 ⋯ c n n

Найдем произведение матрицы А и вектора-столбца В :

Найдем произведение матрицы А и вектора-строку В :

Источник

Произведение двух матриц: формула, решения, свойства

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Произведение матриц: определение, формула, способ нахождения

Определение. Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.

Из этого определения следует формула элемента матрицы C:

Произведение матрицы А на матрицу В обозначается АВ.

Пример 1. Найти произведение двух матриц А и B, если

,

.

Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:

В результате получаем элементы произведения матриц:

Теперь у нас есть всё, чтобы записать произведение двух матриц:

.

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:

Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:

Пример 2. Найти число строк и столбцов матрицы C, которая является произведением двух матриц A и B следующих размерностей:

Примеры нахождения произведения матриц различной размерности

Пример 3. Найти произведение матриц A и B, если:

.

Вычисляем элементы матрицы C = AB.

Найденное произведение матриц: .

Пример 4. Найти произведение матриц и .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 5. Найти произведение матриц A и B, если:

.

Вычисляем элементы матрицы C = AB.

Произведение матриц запишется в виде матрицы-столбца: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 6. Найти произведение матриц A и B, если:

.

Вычисляем элементы матрицы C = AB.

Найденное произведение матриц: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Пример 7. Найти произведение матриц A и B, если:

.

Вычисляем элемент матрицы C = AB.

Произведение матриц является матрицей из одного элемента: .

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке «Компьютеры и программирование».

Возведение матрицы в степень

Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу. Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n-ая степень матрицы путём умножения матрицы на саму себя n раз:

Найти произведение матриц самостоятельно, а затем посмотреть решение

Пример 9. Дана матрица

Найти произведение данной матрицы и транспонированной матрицы , произведение транспонированной матрицы и данной матрицы.

Свойства произведения двух матриц

Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.

Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы

на единичную матрицу справа и слева.

—
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.

Свойство 3. Произведение матриц некоммутативно:
.

Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.

Пример 11. Найти произведения матриц АВ и ВА, если

,

,

и убедиться в том, что эти произведения не равны друг другу:

.

И действительно, найденные произведения не равны:
.

Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.

.

Источник

Как находить произведение матриц. Умножение матриц. Скалярное произведение матриц. Произведение трех матриц

С матрицами (таблицами с числовыми элементами) могут проводиться различные вычислительные действия. Одни из них – умножение на число, вектор, другую матрицу, несколько матриц. Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.

Матрица и число

Начнем с самого простого – с умножения таблицы с числами на конкретную величину. Например, мы имеем матрицу A с элементами aij (i – это номера строк, а j – это номера столбцов) и число e. Произведением матрицы на число e будет матрица B с элементами bij, которые находятся по формуле:

Вам будет интересно: Обомлеть — это что значит? Определение и синонимы

Т. е. для получения элемента b11 нужно взять элемент a11 и умножить его на нужное число, для получения b12 требуется найти произведение элемента a12 и числа e и т. д.

Решим задачу № 1, представленную на картинке. Для получения матрицы B просто умножим элементы из A на 3:

Таким образом, мы получили прямоугольный массив с числовыми элементами.

Векторы и условие существования произведения матриц

В математических дисциплинах существует такое понятие, как «вектор». Под этим термином понимается упорядоченный набор величин от a1 до an. Они называются координатами векторного пространства и записываются в виде столбца. Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.

Векторы можно называть матрицами:

При выполнении над матрицами операций умножения важно помнить о том, что есть условие существования произведения. Вычислительное действие A × B может быть выполнено только тогда, когда число столбцов в таблице A равно числу строчек в таблице B. Итоговая матрица, получаемая в результате вычисления, всегда имеет число строк таблицы A и число столбцов таблицы B.

При умножении не рекомендуется переставлять местами матрицы (множители). Их произведение обычно не соответствует коммутативному (переместительному) закону умножения, т. е. результат операции A × B не равен результату операции B × A. Такая особенность именуется некоммутативностью произведения матриц. В некоторых случаях результат умножения A × B равен результату умножения B × A, т. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.

Умножение на вектор-столбец

Вам будет интересно: Инженерия знаний. Искусственный интеллект. Машинное обучение

При выполнении умножения матрицы на вектор-столбец обязательно учитываем условие существования произведения. Число столбцов (n) в таблице должно совпадать с количеством координат, из которых составлен вектор. Результат вычисления – преобразованный вектор. Его количество координат равно числу строчек (m) из таблицы.

Как вычисляются координаты вектора y, если есть матрица A и вектор x? Для расчетов созданы формулы:

y1 = a11x1 + a12x2 + … + a1nxn,

y2 = a21x1 + a22x2 + … + a2nxn,

ym = am1x1 + am2x2 + … + amnxn,

где x1, …, xn – координаты из x-вектора, m – число строк в матрице и количество координат в новом y-векторе, n – число столбцов в матрице и количество координат в x-векторе, a11, a12, …, amn – элементы матрицы A.

Таким образом, для получения i-й компоненты нового вектора выполняется скалярное произведение. Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.

Решим задачу № 2. Произведение матрицы на вектор найти можно, ведь A имеет 3 столбца, и x состоит из 3 координат. В результате мы должны получить вектор-столбец с 4 координатами. Воспользуемся вышеуказанными формулами:

Умножение вектор-строки на матрицу

Нельзя умножить матрицу, состоящую из нескольких столбцов, на вектор-строку. В таких случаях не выполняется условие существования произведения. А вот умножение вектор-строки на матрицу возможно. Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.

Вычисление первой координаты нового вектора подразумевает умножение вектор-строки и первого вектор-столбца из таблицы. Аналогичным способом производится расчет второй координаты, но вместо первого вектор-столбца берется уже второй вектор-столбец. Вот общая формула для вычисления координат:

yk = a1kx1 + a2kx2 + … + amkxm,

где yk – координата из y-вектора, (k находится в промежутке от 1 до n), m – число строк в матрице и количество координат в x-векторе, n – число столбцов в матрице и количество координат в y-векторе, a с буквенно-цифровыми индексами – элементы матрицы A.

Произведение прямоугольных матриц

Это вычислительное действие может показаться сложным. Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент cij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент cij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.

Теперь разберемся на практике в том, как находить произведение матриц прямоугольного вида. Решим для этого задачу № 3. Условие существования произведения выполняется. Приступим к расчету элементов cij:

Вам будет интересно: Изотоп лития: определение и применение

Элементы рассчитаны. Теперь осталось только составить прямоугольный блок из полученных чисел.

Умножение трех матриц: теоретическая часть

Можно ли найти произведение трех матриц? Эта вычислительная операция выполнима. Результат можно получить несколькими способами. Например, есть 3 квадратных таблицы (одного порядка) – A, B и C. Чтобы вычислить произведение, можно:

Если требуется перемножить матрицы прямоугольного вида, то сначала нужно удостовериться в том, что данная вычислительная операция возможна. Должны существовать произведения A × B и B × C.

Поэтапное умножение не является ошибкой. Есть такое понятие, как «ассоциативность умножения матриц». Под этим термином понимается равенство (A × B) × C = A × (B × C).

Умножение трех матриц: практика

Квадратные матрицы

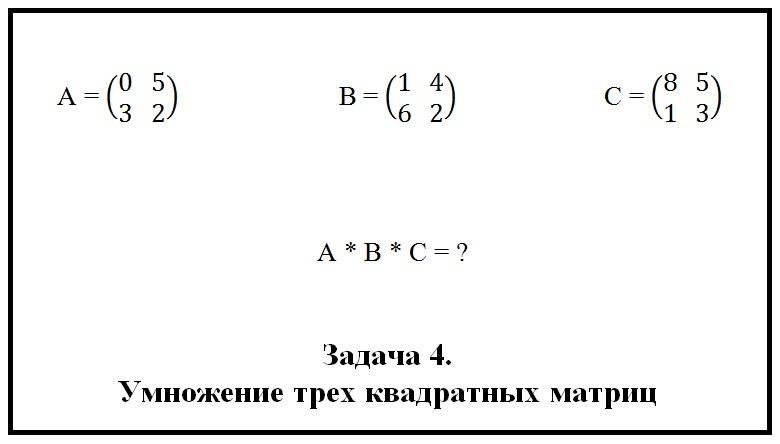
Начнем с умножения небольших квадратных матриц. Ниже на рисунке представлена задача № 4, которую нам предстоит решить.

Будем пользоваться свойством ассоциативности. Перемножим сперва либо A и B, либо B и C. Помним только одно: нельзя переставлять местами множители, т. е. нельзя умножать B × A или C × B. При таком умножении мы получим ошибочный результат.

Шаг первый. Для нахождения общего произведения умножим сначала A на B. При умножении двух матриц будем руководствоваться теми правилами, которые были изложены выше. Итак, результатом умножения A и B будет матрица D с 2 строчками и 2 столбцами, т. е. прямоугольный массив будет включать в себя 4 элемента. Найдем их, выполнив расчет:

Промежуточный результат готов.

Шаг второй. Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:

Таким образом, результатом произведения квадратных матриц является таблица G с вычисленными элементами.

Прямоугольные матрицы

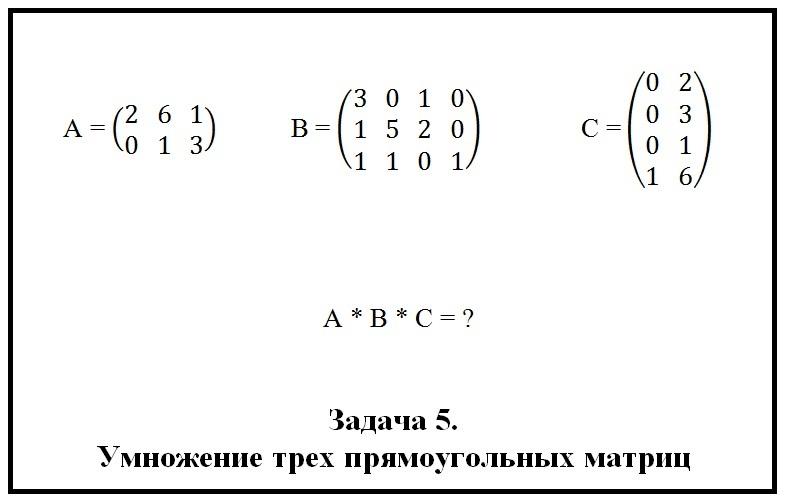
Ниже на рисунке представлена задача № 5. Требуется перемножить прямоугольные матрицы и найти решение.

Проверим, выполняется ли условие существования произведений A × B и B × C. Порядки указанных матриц позволяют нам выполнять умножение. Приступим к решению задачи.

Шаг первый. Умножим B на C для получения D. Матрица B содержит 3 строчки и 4 столбца, а матрица C – 4 строчки и 2 столбца. Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:

Продолжаем решать задачу. В результате дальнейших вычислений мы находим значения d21, d22, d31 и d32. Эти элементы равны 0, 19, 1 и 11 соответственно. Запишем найденные значения в прямоугольный массив.

Шаг второй. Умножим A на D, чтобы получить итоговую матрицу F. В ней будет 2 строчки и 2 столбца. Рассчитаем элементы:

Составим прямоугольный массив, являющийся конечным результатом умножения трех матриц.

Знакомство с прямым произведением

Достаточно сложным для понимания материалом является кронекеровское произведение матриц. У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.

У нас есть 2 квадратные матрицы A, B, которые представлены на картинке. Первая из них состоит из 2 столбцов и 2 строк, а вторая – из 3 столбцов и 3 строк. Мы видим, что матрица, полученная в результате прямого произведения, состоит из 6 строк и точно такого же количества столбцов.

Как при прямом произведении вычисляют элементы новой матрицы? Найти ответ на этот вопрос очень легко, если проанализировать рисунок. Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.

Итоговую матрицу, получаемую прямым произведением, называют блочной. Если вновь проанализировать рисунок, то можно заметить, что наш результат состоит из 4 блоков. Все они включают элементы матрицы B. Дополнительно элемент каждого блока умножен на конкретный элемент матрицы A. В первом блоке все элементы умножены на a11, во втором – на a12, в третьем – на a21, в четвертом – на a22.

Определитель произведения

При рассмотрении темы, касающейся умножения матриц, стоит еще рассмотреть такой термин, как «определитель произведения матриц». Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.

Для матрицы A, состоящей из двух столбцов и двух строчек, определитель легко найти. Существует небольшая формула, представляющая собой разность произведений конкретных элементов:

det A = a11 × a22 – a12 × a21.

Рассмотрим пример вычисления определителя для таблицы второго порядка. Существует матрица A, в которой a11 = 2, a12 = 3, a21 = 5 и a22 = 1. Для вычисления определителя воспользуемся формулой:

det A = 2 × 1 – 3 × 5 = 2 – 15 = –13.

У матриц 3 × 3 определитель вычисляется по более сложной формуле. Она представлена ниже для матрицы A:

det A = a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a11a23a32 – a12a21a33.

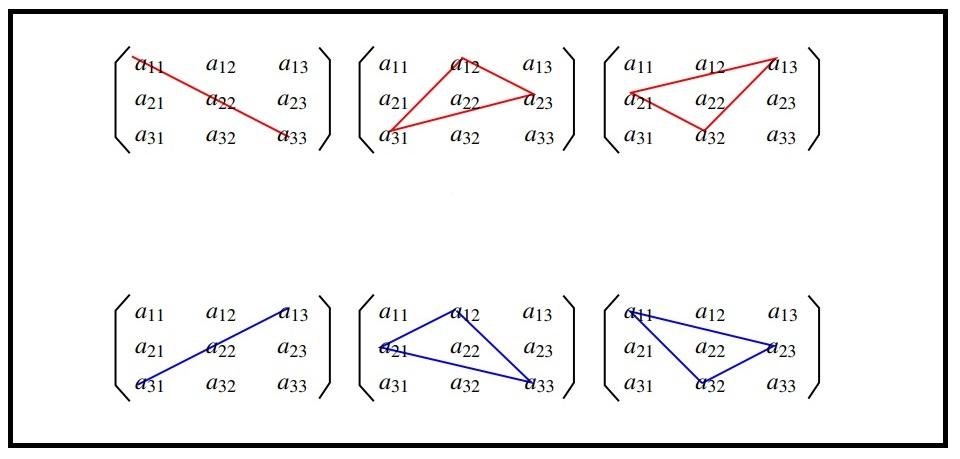
Для запоминания формулы придумали правило треугольника, которое проиллюстрировано на картинке. Сначала умножаются элементы главной диагонали. К полученному значению прибавляются произведения тех элементов, на которые указывают углы треугольников с красными сторонами. Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.

Вам будет интересно: Погранвойска СССР: знаки отличия, функции, структура

Теперь поговорим об определителе произведения матриц. Существует теорема, которая гласит, что данный показатель равен произведению определителей таблиц-сомножителей. Убедимся в этом на примере. У нас есть матрица A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и матрица B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Найдем определители для матриц A и B, произведение A × B и определитель этого произведения.

Шаг первый. Вычислим определитель для A: det A = 2 × 1 – 3 × 1 = –1. Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.

Шаг второй. Найдем произведение A × B. Новую матрицу обозначим буквой C. Вычислим ее элементы:

Шаг третий. Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.

Ранг произведения

Ранг матрицы – это характеристика, отражающая максимальное количество линейно независимых строк или столбцов. Для вычисления ранга выполняют элементарные преобразования матрицы:

После элементарных преобразований смотрят на количество ненулевых строк. Их число – это и есть ранг матрицы. Рассмотрим предыдущий пример. В нем было представлено 2 матрицы: A с элементами a11 = 2, a12 = 3, a21 = 1 и a22 = 1 и B с элементами b11 = 4, b12 = 5, b21 = 1 и b22 = 2. Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.

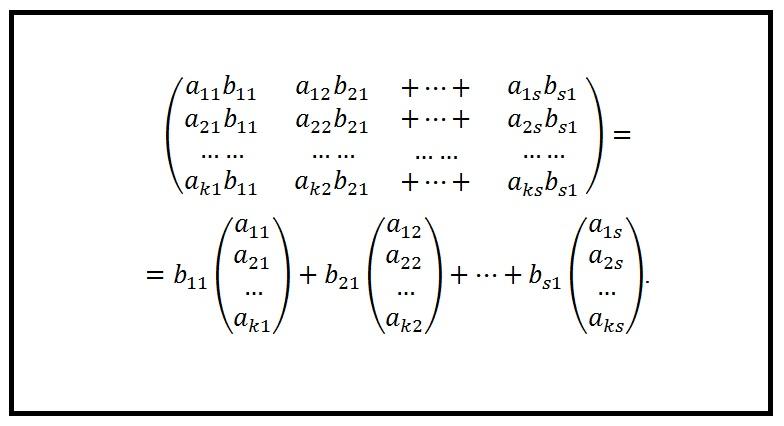
Теперь особое внимание уделим рангу произведения матриц. Существует теорема, которая гласит, что ранг произведения таблиц, содержащих числовые элементы, не превышает ранга любого из сомножителей. Это можно доказать. Пусть A – это матрица размера k × s, а B – это матрица размера s × m. Произведение A и B равно C.

Изучим рисунок, представленный выше. На нем изображен первый столбец матрицы C и его упрощенная запись. Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).

Как находить произведение матриц – достаточно сложная тема. Ее можно легко освоить, но для достижения такого результата придется уделить немало времени заучиванию всех существующих правил и теорем.

Источник