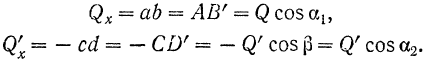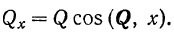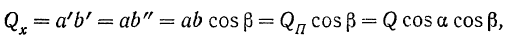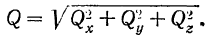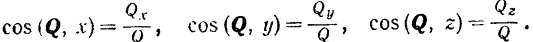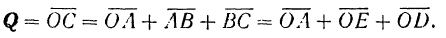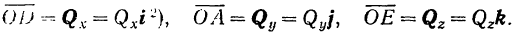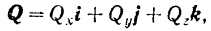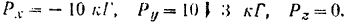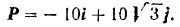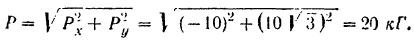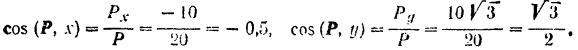Что называется проекцией вектора на заданное направление в пространстве
Угол между векторами. Ортогональные проекции векторов
Угол между векторами
Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Из определения следует, например, что угол между ненулевыми коллинеарными векторами либо равен нулю (если векторы одинаково направлены), либо равен (если векторы противоположно направлены).
Ортогональные проекции векторов
Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу.
Ориентированная прямая с заданным масштабным отрезком называется осью.
Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:
— — ортогональная составляющая вектора относительно вектора ;
— — ортогональная составляющая вектора относительно прямой ;
На рис. 1.23 изображены ортогональные проекции вектора :
— на плоскость вдоль прямой (рис.1.23,в).
На рис. 1.23 изображены ортогональные составляющие вектора :
— относительно оси (вектора ): (рис.1.23,а);
— относительно плоскости (рис.1.23,в).
Для ортогональных проекций справедлива следующая теорема (см. теорему 1.1 в разд. 1.5).
Теорема 1.2 (об ортогональных проекциях вектора).
3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.
Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников и (рис. 1.24,6)).
В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.
Алгебраическое значение длины проекции
Некоторые свойства проекций векторов переносятся на алгебраические значения их длин, в частности:
1. — алгебраическое значение длины ортогональной проекции суммы векторов равно сумме алгебраических значений длин ортогональных проекций слагаемых;
2. — алгебраическое значение длины ортогональной проекции произведения вектора на число равно произведению этого числа на алгебраическое значение длины ортогональной проекции вектора
2. Равенство можно использовать как определение косинуса угла между ненулевыми векторами и (или, что то же самое, косинуса угла между осями, заданными ненулевыми векторами и (рис. 1.26)).
Обозначим через искомые алгебраические значения длин ортогональных проекций.Тогда из равенств
и свойства 1 алгебраических значений длин проекций следует:
Что называется проекцией вектора на заданное направление в пространстве
1. Проекция вектора на заданное направление.
Пусть заданы два вектора `vec a` и `vec b`. Приведём эти векторы к одному началу `O` (рис. 10). Угол, образованный лучами, исходящими из точки `O` и направленными вдоль векторов `vec a` и `vec b`, называют углом между векторами `vec a` и `vec b`. Обозначим этот угол через `alpha`.
Угол `alpha` может принимать различные значения, поэтому в зависимости от знака `cos alpha` проекция может принимать положительные, отрицательные значения или нуль. Например, если угол `alpha` тупой, т. е. больше, чем `90^@`, но меньше `180^@`, то косинус такого угла отрицателен (см. рис. 11).
Проекция равна нулю, если направления векторов `vec a` и `vec b` взаимно перпендикулярны (см. рис. 12).
Проекции равных векторов на любые направления равны друг другу. Проекции противоположных векторов отличаются знаком.
Легко показать, что проекция суммы векторов равна алгебраической сумме их проекций и что при умножении вектора на число его проекция умножается на то же число.
2. Разложение вектора.
Пусть на плоскости задан вектор `vec a` и две пересекающиеся в точке `O` прямые `AO` и `OB` (см. рис. 13).
Вектор `vec a` можно представить в виде суммы двух векторов, направленных вдоль заданных прямых. Для этого параллельным переносом совместим начало вектора `vec a` с точкой `O` пересечения прямых. Из конца вектора `vec a` проведём два отрезка прямых, параллельных `AO` и `OB`. В результате получится параллелограмм. По построению
В чём разница между проекцией вектора на ось и составляющей (компонентой) вектора вдоль этой оси?
Пусть `a = 1`, угол между прямыми `AO` и `OB` равен `varphi = 45^@`, а угол между векторами `vec a` и `vec(a_1)` равен `varphi = 15^@`. Определите модули векторов `vec a_1` и `vec a_2` в разложении (*), а также значения проекций вектора `vec a` на направления `vec(a_1)` и `vec(a_2)` (см. рис. 13).
`a_(a1) = a cos varphi_1
0,97`, `a_(a2) = a cos varphi_2 = cos 30^@
откуда `a_1 = (sin varphi_2)/(sin (varphi_1 + varphi_2)) = (sin 30^@)/(sin 45^@)
и аналогично `a_2 = (sin 15^@)/(sin 45^@)
3. Проектирование вектора на оси координат.
Особенно важен частный случай разложения вектора по двум взаимно перпендикулярным направлениям. Пусть на плоскости задана прямоугольная система координат `xOy` и некоторый вектор `vec a`. Отложим из начала координат вдоль положительного направления осей `Ox` и `Oy` векторы `vec i` и `vec j` соответственно такие, что `|vec i| = 1` и `|vec j| = 1`. Векторы `vec i` и `vec j` назовём единичными векторами.
Перенесём вектор `vec a` так, чтобы его начало совпало с началом координат. Пусть в этом положении он изображается направленным отрезком `AO` (рис. 14).
Числа `a_x` и `a_y` суть проекции вектора `vec a` на направления векторов `vec i` и `vec j` соответственно, то есть на оси `Ox` и `Oy`. Используется и иная, чем (3), форма записи векторов, а именно `vec a = (a_x ; a_y)`.
Пусть угол между положительным направлением оси `Ox` и вектором `vec a` равен `alpha` (рис.14). Тогда `a_x = a cos alpha`, `a_y = a sin alpha`.
В зависимости от значения угла `alpha` проекции вектора `vec a` на оси прямоугольной системы координат могут быть положительными, отрицательными или равными нулю.
Зная проекции вектора `vec a` на оси координат, можно найти его величину и направление по формулам:
`»tg» alpha = (a_y)/(a_x)` (5)
причём знаки `a_x` и `a_y` будут указывать на то, какому квадранту принадлежит значение `alpha`.
4. Пусть теперь нам задано векторное равенство `vec a + vec b = vec c` (рис. 15).
Проектируя все векторы на оси координат, получим очевидные равенства
`c_x = a_x + b_x`, `c_y = a_y + b_y`,
`c_x = a cos alpha + b cos beta`,
`c_y = a sin alpha + b sin beta`,
т. е. по проекциям векторов `vec a` и `vec b` легко находятся проекции суммарного вектора `vec c`.
Проекции вектора на ось и на плоскость
Проекции вектора на ось и на плоскость
Аналитический способ решения задач статики основан на применении метода проекции, знакомого студентам из векторной алгебры. Ввиду особой важности этого метода для дальнейшего, напомним его основы.
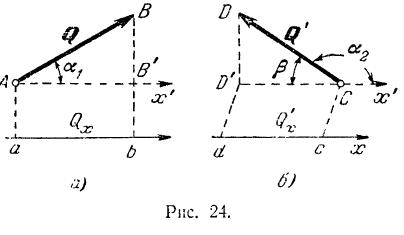
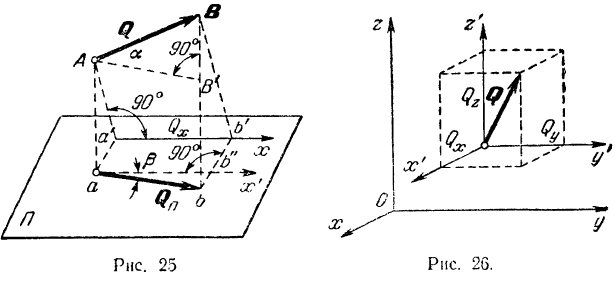
Проекцией вектора на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка оси проекций, заключенного между проекциями на нее начала и конца данного вектора (рис. 24).
Проекция считается положительной, если переход от ее начала к концу совпадает с заданным положительным
направлением оси, и отрицательной — если с противоположным.
Проекцию вектора на ось принято обозначать теми же буквами, что и вектор, но обычного шрифта, указывая нижним индексом ось проекций.
Проекции вектора на две параллельные и одинаково направленные оси равны между собой. Этим особенно удобно бывает пользоваться в тех случаях, когда вектор не лежит в одной плоскости с осью (рис. 24,(5). Из рис. 24, а и б имеем:
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между направлением вектора и положительным направлением оси проекций
Проекция будет положительной, если направление вектора составляет с положительным направлением оси острый угол, н отрицательной — если тупой.
Проекцией вектора на плоскость называется вектор, заключенный между проекциями на эту плоскость начала и конца данного вектора.
Так, например, проекцией_вектора 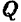
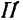
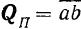
По модулю проекция вектора на плоскость:
где 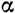
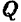
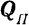
Для нахождения проекции вектора на ось, не лежащую с ним в одной плоскости, иногда бывает удобно
спроектировать сначала вектор на плоскость, в которой лежит эта ось, а затем уже проекцию вектора на плоскость спроектировать на данную ось.
Так, проекция вектора 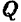
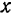
где 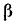
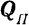
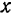
Зная проекции вектора па оси прямоугольной декартовой системы координат, легко найти и модуль и направление вектора.
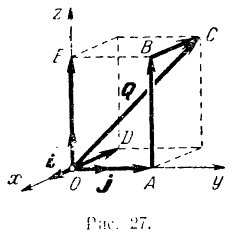
Так как модуль вектора равен диагонали прямоугольного параллелепипеда (рис. 26), ребра которого равны абсолютным значениям проекций вектора на оси координат, то модуль вектора
Модуль вектора равен квадратному корню из суммы квадратов его проекций на три любые взаимно перпендикулярные оси.
Направление вектора определяется из равенств:
Косинус угла между вектором и положительным направлением оси проекции называется направляющим косинусом. Он равен отношению проекции вектора на соответствующую ось к модулю вектора.
Заметим, что в формуле (4) надо брать арифметическое значение корня.
Вектор 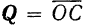
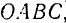
Век горы 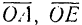
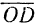
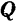
Векторы 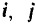
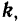
Составляющая вектора по оси координат равна проекции вектора на данную ось, умноженной на соответствующий координатный орт:
Подставляя последние выражения в предыдущее равенство. получаем весьма важную формулу разложения вектора по осям координат
где коэффициенты 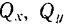
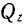
Пример задачи:
Даны проекции силы на оси прямоугольной системы координат
Написать формулу разложения заданной силы по осям координат, а также найти ее модуль и направление.
Решение:
По формуле 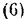
Отсюда, углы между направлением силы и положительными направлениями осей координат:
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).
Проекция вектора на ось. Скалярное произведение векторов
По этой ссылке вы найдёте полный курс лекций по математике:
Опуская из его начала и конца перпендикуляры на заданную ось I, построим на ней направленный отрезок CD (рис. 24). Определение. Проекцией вектора АВ на ось I называется величина направленного отрезка CD, построенного указанным выше способом. Основные свойства проекций 1. Проекция вектора АВ на какую-либо ось I равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25) 2.
Заметив, что (b| cosy> есть проекция вектора b на направление вектора а, можем написать (рис. 27 6) и,аналогично, (рис.27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или Ь — нулевой, будем считать, что Проекция вектора на ось.
Скалярное произведение векторов 5.1.
Свойства скалярного произведения 1. Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и Ь ортогональны, a J.h. Это следует из формулы (1), определяющей скалярное произведение. Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так: 2.
Возможно вам будут полезны данные страницы:
Скалярное произведение векторов, заданных координатами Пусть векторы а и Ь заданы своими координатами в ортонор миро ванном базисе Рассмотрим скалярное произведение векторов и и Ь: Проекция вектора на ось. Скалярное произведение векторов Пользуясь распределительным свойством скалярного произведения, находим Учитывая, что Тоесть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат. Пример.
| Найти скалярное произведение векторов |
Тогда формула (7) примет следующий вид cos Пример. Найти угол между векторами Пользуясь формулой (8), находом Пусть b = i, т.е. b = <1,0, 0>. Тогда для всякого вектора О имеем Проекция вектора на ось. Скалярное произведение векторов или, в координатной записи, где q есть угол, образованный вектором а с осью Ох.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.