Что называется приведенной длиной физического маятника

Что называется приведенной длиной физического маятника

Чему равна приведенная длина физического маятника?

Савельев И.В, т.1, стр. 197

Из сопоставления формул (54.6) и (54.11) получается, что математический маятник с длиной

будет иметь такой период колебаний, как и физический маятник. Величину (54.12) называют приведенной длиной физическогомаятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Яворский Б.М. Детлаф А.А., Справочник по физике, 1985 г. стр. 261

Приведенной длиной физического маятника l_пр, называется длина матматического маятника, имеющего такой же период колебаний:

Где J_C – момент инерции физического маятника относительно оси, проходящей через центр инерции С маятника и параллельной его оси качания.

где L=J/(ml) — приведенная длина физического маятника.

приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с пери­одом колебаний данного физического маятника.

Источник

Приведенная длина

Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника.

Приведённая длина вычисляется следующим образом: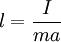

где I — момент инерции относительно точки подвеса, m — масса, a — расстояние от точки подвеса до центра масс.

Литература

Смотреть что такое «Приведенная длина» в других словарях:

Приведенная длина, мм (см) — lпр Источник: Поправка к ГОСТ 14249 89: оригинал документа … Словарь-справочник терминов нормативно-технической документации

Приведенная длина, мм (см) — lпр Источник: ГОСТ 14249 89: Сосуды и аппараты. Нормы и методы расчета на прочность оригинал документа … Словарь-справочник терминов нормативно-технической документации

приведенная длина стержня — Условная длина однопролетного стержня, критическая сила которого при шарнирном закреплении его концов такая же, как для заданного стержня. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно… … Справочник технического переводчика

приведенная длина физического маятника — Длина математического маятника, имеющего такой же период колебаний, как и физический маятник. [ГОСТ 24284 80] Тематики гравиразведка и магниторазведка Обобщающие термины приборы и их характеристики … Справочник технического переводчика

приведенная длина вала — Длина прямолинейного вала постоянного сечения, эквивалентного по жесткости коленчатому валу, или его части, или какому либо валу с различными формами его отдельных элементов … Политехнический терминологический толковый словарь

ДЛИНА ПУТЕЙ — различается: развернутая, исчисляемая как сумма длин всех главных путей (первых, вторых, третьих и т. д.), и станционная. В учетной и плановой практике различают развернутую длину главных и станционных путей. Длина станционных путей измеряется… … Технический железнодорожный словарь

длина стержня приведенная — Условная длина сжатого стержня с заданными условиями закрепления его концов, длина которого по значению критической силы эквивалентна длине стержня с шарнирно закреплёнными концами [Терминологический словарь по строительству на 12 языках (ВНИИИС… … Справочник технического переводчика

приведенная режущая способность абразивного инструмента — приведенная режущая способность Отношение режущей способности абразивного инструмента к одному из параметров его контакта с обрабатываемой поверхностью. Примечания 1. Параметрами контакта являются линейная сила прижима абразивного инструмента,… … Справочник технического переводчика

приведенная скорость изнашивания абразивного инструмента — приведенная скорость изнашивания Отношение скорости изнашивания абразивного инструмента к одному из параметров его контакта с обрабатываемой поверхностью. Примечания 1. Параметрами контакта являются линейная сила прижима абразивного инструмента,… … Справочник технического переводчика

ДЛИНА СТЕРЖНЯ ПРИВЕДЕННАЯ — условная длина сжатого стержня с заданными условиями закрепления его концов, длина которого по значению критической силы эквивалентна длине стержня с шарнирно закреплёнными концами (Болгарский язык; Български) приведена дължина на прът (Чешский… … Строительный словарь

Источник

Физический маятник

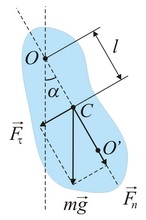
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции. В положении равновесия центр инерции маятника С находится под точкой подвеса маятника O, на одной с ней вертикали (рис. 50). При отклонении маятника от положения равновесия на угол α возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m – масса маятника, а l – расстояние между точкой подвеса и центром инерции маятника. Знак «–» означает, что вращательный момент стремится вернуть маятник в положение равновесия, т. е. направлен в сторону, противоположную изменения угла Δα. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой J, можно написать:

. (136)

(137)

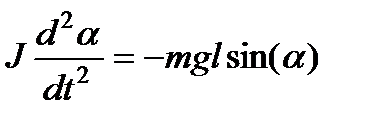
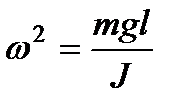
Тогда для малых отклонений, когда выполняется условие sin(α) ≈ α, получаем уравнение гармонических колебаний:

. (138)

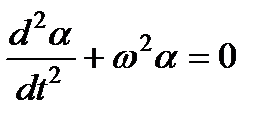
При малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, циклическая частота которых определяется формулой (137). Соответственно, период колебаний физического маятника равен:

. (139)

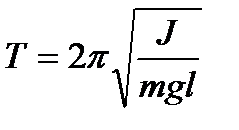
Из сопоставления формул (139) и (134) следует, что математический маятник с длиной

(140)

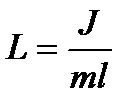
будет иметь такой период колебаний, как и данный физический маятник. Величину (140) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку О’ на рис. 50).

По теореме Штейнера момент инерции маятника l может быть представлен в виде

где J₀ – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника. Подставив (141) в формулу (140), получаем:

. (142)

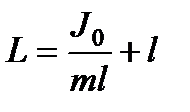
Из (142) следует, что приведенная длина всегда больше l, так что точка подвеса и центр качания лежат по разные стороны от центра инерции.

Подвесим маятник в точке, совпадающей с центром качания О’. В соответствии с (142) приведенная длина в этом случае будет равна

(143)

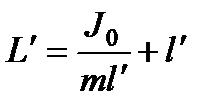
где l’ – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l’ = L – l, выражение (143) можно записать следующим образом:

.

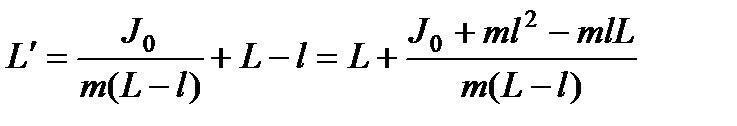
Поскольку J₀ + ml 2 равно моменту инерции относительно первоначальной оси вращения J, и этой же величине, согласно (140) равно выражение mlL, то числитель дроби будет равен нулю. Поэтому L’ = L. Это означает, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Это положение называется теоремой Гюйгенса:

Источник

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник

Приведённая длина физического маятника

Сравним периоды колебаний математического и физического маятников:

; .

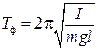
Видно, что комбинация параметров физического маятника I/(ml) имеет размерность длины. Она называется приведённой длиной физического маятника:

Определение 1. Приведённой длиной физического маятника называется длина математического маятника, изохронного данному физическому.

Определение 2. Точка О’, находящаяся на расстоянии от оси О на линии, проходящей через центр масс С, называется центром качания физического маятника (рис. 9.7).

Центр качания О’ обладает одним замечательным свойством: если ось качания пропустить через точку О’, то период качания Т_О’ = Т_О, т. е. точки О и О’ являются изохронными центрами качания.

Так например, приведённая длина кольца из Примера 1 l_пр = 2R; приведённая длина стержня из Примера 2 l_пр = (2/3)а.

Источник