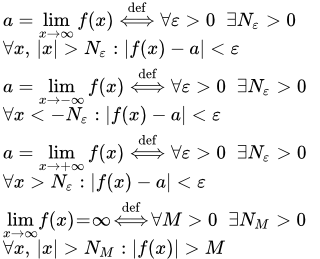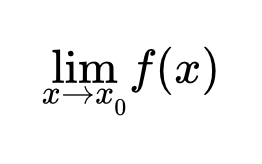Что называется пределом функции в точке и на бесконечности

Определение предела функции на бесконечности

Конечный предел функции на бесконечности

Также часто используется следующее обозначение:
.

Запишем это определение, используя логические символы существования и всеобщности:
.
Здесь подразумевается, что значения принадлежат области определения функции.

Односторонние пределы

Часто встречаются случаи, когда функция определена только для положительных или отрицательных значений переменной x (точнее в окрестности точки или ). Также пределы на бесконечности для положительных и отрицательных значений x могут иметь различные значения. Тогда используют односторонние пределы.

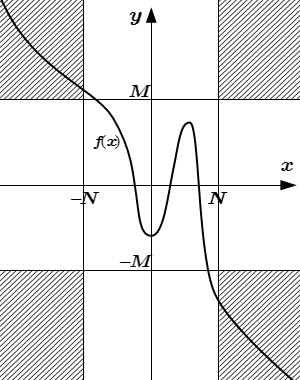
Бесконечный предел функции на бесконечности

С помощью логических символов существования и всеобщности, определение бесконечного предела функции можно записать так:
.

Аналогично вводятся определения бесконечных пределов определенных знаков, равных и :
.
.

Определения односторонних пределов на бесконечности.
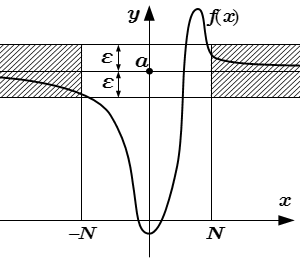
Левые пределы.
.
.
.
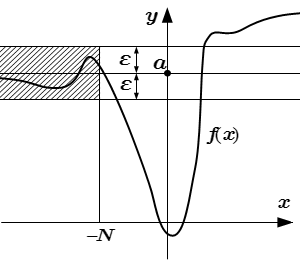
Правые пределы.
.
.
.

Определение предела функции по Гейне

Определения предела по Гейне и Коши эквивалентны.

Примеры

Пример 1

Все примеры ⇑ Используя определение Коши показать, что
.

Выпишем определение конечного предела функции на бесконечности по Коши:
.
Преобразуем разность:
.
Разделим числитель и знаменатель на и умножим на –1 :
.

Пример 2

1) Решение при x стремящемся к минус бесконечности

2) Решение при x стремящемся к плюс бесконечности

Преобразуем исходную функцию. Умножим числитель и знаменатель дроби на и применим формулу разности квадратов:
.
Имеем:

.
Выпишем определение правого предела функции при :
.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Предел функции

п.1. Предел функции в точке и на бесконечности

п.2. Свойства предела функции

1. Одна и та же функция в одной и той же точке может иметь только один предел: \begin \left. \begin \lim_f(x)=a\\ \lim_f(x)=b \end \right\> \Rightarrow a=b \end 2. Если функция непрерывна, то её предел в точке \(x_0\) совпадает со значением функции в этой точке: \begin \lim_f(x)=f(x_0) \end 3. Если функция «зажата» между двумя другими функциями, имеющими одинаковый предел \(a\), то предел этой функции также равен \(a\): \begin \left. \begin g(x)\leq f(x)\leq h(x)\\ \lim_g(x)=a\\ \lim_h(x)=b \end \right\> \Rightarrow \lim_f(x)=a \end 4. Операция перехода к пределу сохраняет нестрогие неравенства: \begin \left. \begin f(x)\leq g(x)\\ \lim_f(x)=a\\ \lim_g(x)=b \end \right\> \Rightarrow a\leq b \end 5. Переход к пределу для строгих неравенств в общем случае приводит к нестрогому неравенству: \begin \left. \begin f(x)\lt g(x)\\ \lim_f(x)=a\\ \lim_g(x)=b \end \right\> \Rightarrow a\leq b \end 6. Предел суммы (разности, произведения, частного) равен сумме (разности, произведению, частному) пределов: \begin \left. \begin \lim_f(x)=a\\ \lim_g(x)=b \end \right\> \Rightarrow \lim_(f(x)\pm g(x))=a\pm b \\ \left. \begin \lim_f(x)=a\\ \lim_g(x)=b \end \right\> \Rightarrow \lim_(f(x)\cdot g(x))=a\cdot b \\ \left. \begin \lim_f(x)=a\\ \lim_g(x)=b\ne 0 \end \right\> \Rightarrow \lim_\left(\frac\right)=\frac ab \end

п.3. Раскрытие неопределенностей \(\left[\frac<\infty><\infty>\right]\) и \(\left[\infty-\infty\right]\)

Для пределов функций правила раскрытия неопределенностей \(\left[\frac<\infty><\infty>\right]\) и \(\left[\infty-\infty\right]\) аналогичны правилам для пределов последовательностей (см. §37 данного справочника).

п.4. Раскрытие неопределенности \(\left[\frac00\right]\)

п.5. Примеры

Пример 1. Докажите, используя определение предела функции в точке:
a) \( \lim_(3x+1)=4 \)

Таким образом, для любого сколь угодно малого ε>0 мы находим \(\delta(\varepsilon)=\frac<\varepsilon><3>\), при этом из \(0\lt|x-1|\lt\delta(\varepsilon)\Rightarrow |(3x+1)-4|\lt\varepsilon\).
Что и требовалось доказать.

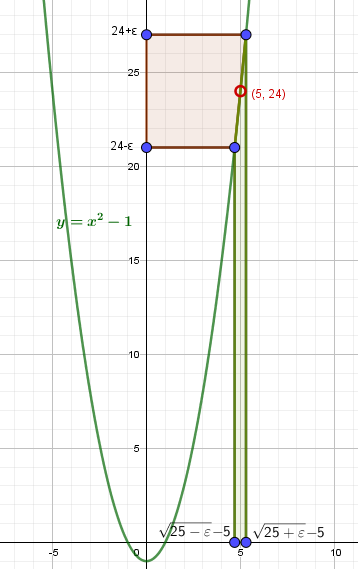Пусть \(\varepsilon\gt 0\) – сколь угодно малое число. Найдем множество значений x, для которых \(|f(x)-a|\lt \varepsilon\).

Выбираем в качестве \(\delta(\varepsilon)\) меньшую оценку \(\delta_2\): \begin \delta(\varepsilon)=min(5-\sqrt<25-\varepsilon>;\sqrt<25+\varepsilon>-5)=\delta_2=\sqrt<25+\varepsilon>-5\\ 0\lt|x-5|\lt\sqrt<25+\varepsilon>-5\\ \delta(\varepsilon)=\sqrt<25+\varepsilon>-5 \end Например:

Таким образом, для любого сколь угодно малого ε>0 мы находим \(\delta(\varepsilon)=\sqrt<25+\varepsilon>-5\), при этом из \(0\lt|x-1|\lt\delta(\varepsilon)\Rightarrow |(x^2-1)-24|\lt\varepsilon\).
Что и требовалось доказать.

Источник

Предел функции – определения, теоремы и свойства

Определение предела функции

Первое определение предела функции по Гейне

С помощью логических символов существования и всеобщности это определение можно записать следующим образом:

.
См. «Универсальное определение предела функции по Гейне и по Коши».

Второе определение по Коши

Здесь a и x ₀ также могут быть как конечными числами, так и бесконечно удаленными точками. С помощью логических символов существования и всеобщности это определение можно записать следующим образом:
.

Если в качестве множества взять левую или правую окрестность конечной точки, то получим определение предела по Коши слева или справа.

Теорема
Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство

Применяемые окрестности точек

Далее мы приводим формулировки определений предела функции по Коши для разных случаев, используя определения окрестностей с равноудаленными концами.

Конечные пределы функции в конечных точках

С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.

Конечные пределы функции в бесконечно удаленных точках

Аналогичным образом определяются пределы в бесконечно удаленных точках.
.
.
.

Бесконечные пределы функции

Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.

Свойства и теоремы предела функции

Основные свойства

Функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке равные односторонние пределы.

Если на некоторой проколотой окрестности точки x ₀ :
,
и существуют конечные (или бесконечные определенного знака) равные пределы:
, то
.

Доказательства основных свойств приведены на странице
«Основные свойства предела функции».

Арифметические свойства предела функции

Доказательства арифметических свойств приведены на странице
«Арифметические свойства предела функции».

Критерий Коши существования предела функции

Предел сложной функции

Доказательство теоремы приводится на странице
«Предел и непрерывность сложной функции».

Бесконечно малые и бесконечно большие функции

Бесконечно малые функции

Доказательства свойств изложены в разделе
«Свойства бесконечно малых функций».

Бесконечно большие функции

Свойства бесконечно больших функций

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».

Пределы монотонных функций

Отсюда следует, что строго возрастающая функция также является неубывающей. Строго убывающая функция также является невозрастающей.

Аналогичная теорема для невозрастающей функции.

Доказательство теоремы изложено на странице
«Пределы монотонных функций».

Определение функции, верхней и нижней грани

Элемент x ∈ X называют аргументом функции или независимой переменной.
Элемент y ∈ Y называют значением функции или зависимой переменной.

Если это особо не оговорено, мы рассматриваем функции, области определения и множества значений которых принадлежат множеству действительных чисел.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Предел функции

Из Википедии — свободной энциклопедии

Преде́лом фу́нкции (предельным значением функции) в точке, предельной для области определения функции, называется такая величина, к которой значение рассматриваемой функции стремится при стремлении её аргумента к данной точке. Одно из основных понятий математического анализа.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в любой окрестности данной точки существуют точки области определения. Это позволяет говорить о стремлении аргумента функции к данной точке. При этом предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо конкретно указывать способ сходимости функции, для чего вводят так называемую базу подмножеств области определения функции, и тогда определение предела функции формулируют по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Также благодаря рассмотрению расширенной вещественной прямой (на которой базу окрестностей можно построить и для бесконечно удалённой точки) можно определить такие понятия, как предел функции при стремлении аргумента к бесконечности, а также стремление самой функции к бесконечности. Предел последовательности (как предел функции натурального аргумента) как раз представляет собой пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции в точке означает, что для любого заданного значения области значений можно подобрать такую окрестность этого значения, что в любой сколь угодно малой окрестности точки, в которой функция принимает заданное значение, существуют точки, значение функции в которых окажется за пределами указанной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной в данной точке.

Источник

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

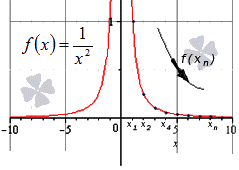
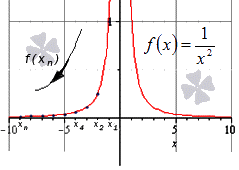
При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

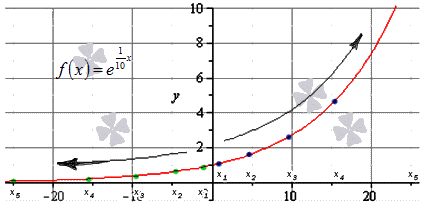
Решение

Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник