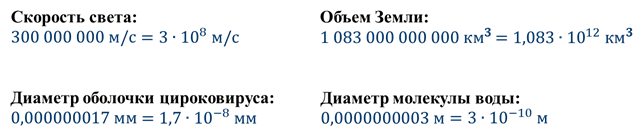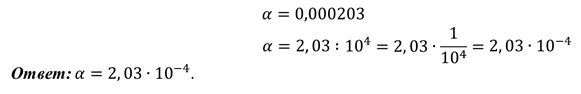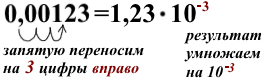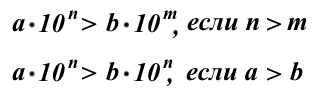Что называется порядком числа
Стандартная форма записи числа, мантисса числа, порядок числа
Положительное число, записанное в стандартной форме, имеет вид
,
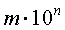
Число m является натуральным числом или десятичной дробью, удовлетворяет неравенству
,
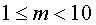
и называется мантиссой числа, записанного в стандартной форме.
Число n является целым числом (положительным, отрицательным или нулем) и называется порядком числа, записанного в стандартной форме.
Например, число 3251 в стандартной форме записывается так:
,
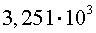
Здесь число 3,251 является мантиссой, а число 3 является порядком.
Стандартная форма записи числа часто используется в научных расчетах и очень удобна для сравнения чисел.
Для того, чтобы сравнить два числа, записанных в стандартной форме, нужно сначала сравнить их порядки. Большим будет то число, порядок которого больше. Если же порядки сравниваемых чисел одинаковы, то нужно сравнить мантиссы чисел. Большим в этом случае будет то число, у которого мантисса больше.
Например, если сравнить между собой записанные в стандартной форме числа
и 
,
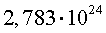
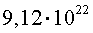
то, очевидно, первое число больше второго, поскольку у него порядок больше.
Если же сравнить между собой числа
и 
,
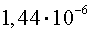
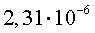
то, очевидно, что второе число больше, чем первое, поскольку порядки у этих чисел совпадают, а мантисса у второго числа больше.
Порядок (математика)
Порядок в широком смысле слова — гармоничное, ожидаемое, предсказуемое состояние или расположение чего-либо.
Специализированные варианты использования слова:
Математика
Смотреть что такое «Порядок (математика)» в других словарях:
Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия
Порядок группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Порядок элемента — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Порядок элемента группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия
Математика в Древнем Египте — Данная статья часть обзора История математики. Статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э. Древнейшие древнеегипетские математические тексты относятся к началу II… … Википедия
Математика инков — Кипукамайок из книги Гуамана Пома де Айяла «Первая Новая Хроника и Доброе Правление». Слева у ног кипукамайока юпана, содержащая вычисления священного числа для песни «Сумак Ньюста» (в оригинале рукописи рисунок не цветной, а чёрно белый;… … Википедия
Группа (математика) — Теория групп … Википедия
Список эпизодов телесериала «Закон и порядок» — В данной таблице представлен список эпизодов американского телесериала «Закон и порядок». Первая серия была показана 13 сентября 1990 года на канале NBC. На данный момент вышло 20 сезонов сериала. Всего снято 456 эпизода. В 2010 году сериал… … Википедия
Алгебраический порядок точности численного метода — (порядок точности численного метода, степень точности численного метода, порядок точности, степень точности) наибольшая степень полинома, для которой численный метод даёт точное решение задачи. Другое определение: говорят, что численный… … Википедия
Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
Стандартный вид числа
Урок 36. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Стандартный вид числа»
Наверняка, в физике, биологии, химии или географии вы сталкивались, как с очень большими, так и очень малыми положительными числами.
Скажите с такими числами удобно выполнять математические расчёты? Конечно же, нет. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. В таком случае полезным оказывается представление числа в виде
Говорят, что мы записали числа в стандартном виде. В таком виде можно представить любое положительное число.
Стандартным видом числа 
называют его запись в виде: 
, где 
и 
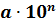
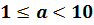
– целое число.
Число называется порядком числа .
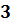
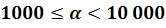
Если порядок числа равен 
, то это означает, что 
.
Если порядок числа равен 
, то это означает, что 
.
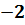
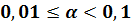
Большой положительный порядок показывает, что число очень велико.
Большой по модулю отрицательный порядок показывает, что число очень мало.
, где и – целое число
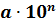
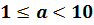
По определению стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра.
Все остальные цифры должны стоять после (справа) от запятой.
Порядок числа даёт представление о том, насколько велико или мало это число.
В стандартном виде можно записать не только большое или малое, но и любое число.
Для того чтобы привести число к стандартному виду, надо:
1. Перенести в нём запятую так, чтобы она была сразу после первой значащей цифры.
2. полученное число умножить на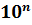 
, где подбирается так, чтобы произведение было равно данному числу.
Значащей цифрой числа называют его первую (слева направо) отличную от нуля цифру, а также все последующие за ней цифры.
Пример: представим в стандартном виде число.
Задание: запишите число в стандартном виде.
Задание: запишите в стандартном виде число, равное значению произведения х и у.
Стандартным видом числа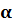 
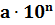
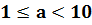
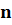
называют его запись в виде: 
, где 
и 
– целое число.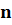
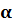
Число называется порядком числа .
Для того, чтобы привести число к стандартному виду, надо перенести в нём запятую так, чтобы она была сразу после первой значащей цифры, и полученное число умножить на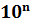 
, где подбирается так, чтобы произведение было равно данному числу.
Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.
Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.
Любое рациональное число может быть представлено в виде:
 |  |
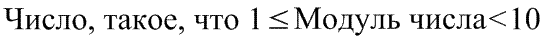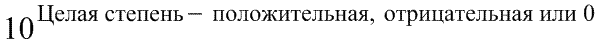| Эта часть записи называется Мантиссой числа в стандартной (научной) форме. | А эта часть называется Порядком числа в стандартной (научной) форме. |
Пример 2 : Величины 890 и 45932, записанные в стандартной форме выглядят как: 8,9*10 2 и 4,5932*10 4 и отличаются на 2 порядка = имеют разницу в 2 порядка. Числа 7,5 и 75 различаются на порядок ( на 1 порядок) = имеют разницу в 1 порядок, что бы там в телевизоре не думали. И так далее.
Очевидно, что при сложении и вычитании чисел записанных в стандартной форме и имеющих один порядок, достаточно сложить или вычесть мантиссы.
Пример 3: 7,2*10 34 + 1,2*10 34 = (7,2+ 1,2)*10 34 =8,4*10 34
Пример 4: 9,9*10 13 + 9,9*10 12 =9,9*10 13 + 0,99*10 13 = (9,9+ 0,99)*10 13 =10,89*10 13 =1,089*10 14
Очень удобно проводить операции умножения и деления с числами, записанными в стандартной форме, пользуясь правилами действий со степенями:
Пример 5: 4,0*10 3 x 2,25*10 2 =(4,0×2,25)x(10 3+2 )= 9,0*10 5
Пример 6: 5,0*10 6 /2,5*10 3 =(5,0/2,5)x(10 6-3 )= 2,0*10 3
Стандартный вид числа
Стандартный вид числа — это его запись в виде произведения
Число n называется порядком числа, записанного в стандартном виде.
В стандартном виде можно записать любое положительное число.
Как правило, стандартный вид числа используют для записи больших и малых величин.
Записать число в стандартном виде и указать порядок числа:
Чтобы записать число в стандартном виде, надо представить его в виде произведения, первый множитель которого — число от единицы до десяти (1≤a 
Получили число, записанное в стандартном виде. Его порядок n=6.
При решении примеров на приведение числа к стандартному виду удобнее деление числа на
заменить умножением на
Итак, для приведения к стандартному виду числа, больше либо равного 10, запятую в его записи переносим влево на n цифр и результат умножаем на 10 в степени n:
2) 12 346 000 000=12 346 000 000,
Чтобы величина первого множителя входила в промежуток от 1 до 10, надо запятую в записи данного числа перенести на 10 знаков влево, а чтобы число не изменилось, умножить результат на 10¹º:
Это число записано в стандартном виде. Его порядок n=10.
Чтобы первый множитель соответствовал условию 1≤a 
Число 5430 представляем в стандартном виде. Для этого запятую в его записи переносим на 3 цифры влево и результат умножаем на 10³.
Далее выполняем умножение степеней с одинаковыми основаниями.
Сравнение чисел, записанные в стандартном виде
9,8 \cdot 10^7 \]» title=»Rendered by QuickLaTeX.com»/>
так как порядок первого числа больше порядка второго числа (8>7);
поскольку порядок первого числа меньше порядка второго числа (-8 
2,97 \cdot 10^9 \]» title=»Rendered by QuickLaTeX.com»/>
так как при равных порядках первый множитель у первого числа больше, чем у второго (3,4>2,97).