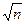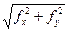Что называется относительной невязкой теодолитного хода
Тема: Основы математической обработки результатов теодолитной съёмки. Вычисление координат вершин теодолитного хода. Составление плана
1. Проверка полевых вычислений и определение поправок в измерения длин линий
_______ Далее вычисляются средние значения длин линии:
 |
_______ В каждую длину линии вводятся поправки по формуле:
 |
_______ Поправки вводятся при:
 |
_______ После уравнивания углов производится вычисление дирекционных углов всех сторон теодолитного хода. _______ Вычисленные дирекционные углы переводятся в румбы.
2. Связь между дирекционными углами и горизонтальными углами теодолитного хода
 |
 |
_______ Дирекционный угол линии последующей равен дирекционному углу линии предыдущей плюс 180 0 минус угол вправо по ходу лежащий.
3. Обработка угловых измерений замкнутого теодолитного хода
 |
 |
_______ где fβ – угловая невязка.
 |
_______ где n –вершина углов, следовательно:
 |
4. Угловая невязка разомкнутого теодолитного хода
 |
Для вычисления ∑β теор. найдем дирекционные углы всех сторон хода:
 |
 |
 |
 |
_______ где αнач. и αкон. – дирекционные углы сторон опорной сети, тогда:
 |
5. Невязки в диагональном ходе
 |
 |
_______ После обработки угловых измерений вычисляются дирекционные углы и румбы всех сторон хода.
6. Прямая и обратная геодезические задачи
6.1. Прямая геодезическая задача: по координатам отрезка прямой (начала), его длине и направлению определить координаты конца отрезка
 |
 |
_______ Прямая геодезическая задача применяется при вычислении координатных точек теодолитного хода.
6.2. Обратная геодезическая задача: по координатам начала и конца отрезка прямой найти его длину и направление
 |
 |
_______ Далее вычисляют arctg и находят числовое значение румба. Название румба определяют по знакам приращений координат, от румба переходят к дирекционному углу.
Длина линии может быть найдена по следующим формулам:
 |
_______ Обратная геодезическая задача применяется при подготовке данных для перенесения проектов сооружений в натуру.
7. Уравнивание приращений координат
_______ Уравниванием называется совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений.
_______ Уравнивание проводится для устранения невязок, обусловленных наличием ошибок в избыточно измеренных величинах, и для определения вероятнейших значений искомых неизвестных или их значений, близких к вероятнейшим. В процессе уравнвиания это достигается путём определения поправок к измеренным величинам (углам, направлениям, длинам линий или превышениям).
7.1. Вычисление координат точек теодолитного хода
 |
_______ Из решения прямой геодезической задачи по известным длинам сторон и румбам вычисляются приращения координат для каждой стороны хода по формулам:
 |
_______ Далее вычисляются невязки в приращениях координат замкнутого хода.
7.2. Вычисление невязок в приращениях координат замкнутого хода
_______ Из геометрии известно, что сумма проекций сторон многоугольника на любую ось равна нулю, следовательно:
 |
_______ Под влиянием ошибок измерений замкнутый полигон будет разомкнутым на величину fр – абсолютная невязка в периметре полигона.
 |
 |
_______ Если полученная невязка недопустима, то необходимо произвести повторное измерение длин линий.
_______ Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме – в данном случае равна нулю.
7.3. Вычисление невязок в приращениях координат разомкнутого теодолитного хода
_______ Определение допустимости невязок и их распределения производится так же, как для замкнутого теодолитного хода.
 |
 |
Для диагонального хода, например:
 |
 |
_______ По исправленным значениям приращений координат вычисляются координаты всех точек хода по формулам:
 |
8. Построение плана
_______ Построение плана выполняются в следующей последовательности :
1) построение координатной сетки,
2) нанесение вершин теодолитного хода по координатам,
3) нанесение на план контуров местности,
4) оформление плана.
8.1. Построение координатной сетки
_______ 1) построение сетки с помощью линейки Дробышева:
 |
_______ Построение сетки основано на построении прямоугольного треугольника с катетами 50×50 см и гипотенузой 70,711 см ;
2) построение сетки с помощью циркуля, измерителя и масштабной линейки:
 |
_______ Вершины теодолитного хода наносятся на план по координатам относительно сетки с помощью измерителя и поперечного масштаба.
_______ Контроль правильности построения точек выполняется по известным расстояниям между точками. Допустимое расхождение – 0,3 мм в масштабе плана.
_______ Контуры местности наносятся на план в соответствии с абрисами.
_______ Оформление плана выполняется в строгом соответствии с условными знаками, установленными для данного масштаба.
Вычисление линейных невязок по осям координат



Камеральная обработка результатов измерения теодолитного хода
Вычисление координат точек теодолитного хода.
Перед началом вычисления проверяют все журналы (значения вычисленных горизонтальных и вертикальных углов, горизонтальных проложений). Уравнивают горизонтальные углы, для этого вычисляют сумму измеренных горизонтальных углов:
Вычисляют теоретическую сумму углов
Σβт=180º(n–2) – для замкнутого хода
n – число измеренных углов
Вычисляют угловую невязку: fβ= Σβф– Σβт сравнивая ее с допустимой: fβ доп =1.5t
где t–точность отсчетного приспособления теодолита.
Невязка fβ по абсолютной величине не должна превышать допустимого значения fβ доп, в противном случае углы измеряют заново. Если условие вычисляют поправку в каждый угол и записывают в ведомость над значениями измеренных углов: δβ=– fβ/n.
Контролем правильности распределения невязки служит равенство: Σδβ=– fβ
Для контроля подсчитывают сумму исправленных углов, которая должна быть равна теоретической сумме углов: Σβиспр= Σβт
Примычный угол βприм не исправляют.
Вычисление дирекционных углов и румбов.
По исходному дирекционному углу αпт–I и исправленным значениям углов определяют дирекционные углы сторон теодолитного хода:
Контролем правильности вычислений дирекционных углов является совпадение значения дирекционного угла начальной стороны αI–II:
| № четв. | Дирекционный угол | Назв. румба | Формулы | Знаки приращения | |
| ∆x | ∆y | ||||
| I | 0º–90º | СВ | r=α | + | + |
| II | 90º–180º | ЮВ | r=180º–α | – | + |
| III | 180º–270º | ЮЗ | r=α–180º | – | – |
| IV | 270º–360º | СЗ | r=360º–α | + | – |
Вычисление приращений координат
По значениям дирекционных углов и горизонтальными проложениям сторон теодолитного хода вычисляют приращения координат с точностью до 0.01м:
Знаки приращения координат определяют в зависимости от названия румба.
Вычисление линейных невязок по осям координат
Находят суммы вычисленных приращений
И теоретические суммы приращений
Линейные невязки по осям координат
Вычисление абсолютной и относительной невязок теодолитного хода
fабс =
Определяют относительную линейную невязку fотн теодолитного хода: fотн=
где Р – периметр хода.
Допустимое значение относительной невязки не должно превышать погрешности линейных измерений 
Поправки округляют до 0.01 мм и выписывают их со своими знаками над соответствующими приращениям ∆х и ∆у.
Сумма поправок должна равняться невязке с обратным знаком:
Вычисляют исправленные приращения координат и записывают результаты в ведомость:
Для контроля определяют суммы исправленных приращений координат, которые должны быть равны теоретическим суммам приращений:
Обработка углов замкнутого и разомкнутого теодолитных ходов
В замкнутом теодолитном ходе при безошибочном измерении горизонтальных углов их сумма равна

где n – число вершин многоугольника.
Так, для пятиугольника I–II–III–IV–V на рис. 65
Угловые измерения сопровождаются погрешностями, поэтому сумма измеренных углов Σβи отличается от теоретической суммы.
Рис. 65. Замкнутый I–II–III–IV–V и разомкнутый V–A–B–II
теодолитные ходы
Разность между суммой измеренных углов и теоретической суммой называется угловой невязкой:

Угловая невязка должна быть меньше или равна допустимой, т. е
где τ – точность отсчетного приспособления теодолита.
Если указанное условие не выполняется, то при правильных вычислениях углы перемеряют в поле.
При выполнении этого условия угловую невязку распределяют на все измеренные углы поровну, округляя до точности τ. Сумма исправленных углов должна равняться теоретической сумме.
Вычислим угловую невязку на примере разомкнутого теодолитного хода V–A–B–II (рис. 65), в котором измерены углы на точках А и В. Сумма этих углов составляет Σβи. Теоретическая сумма составляет Σβт = bА+ bВ.
Углы bА и bВ используются при вычислении дирекционных углов aА-В и aВ-II:
где aА-В – дирекционный угол начальной стороны разомкнутого теодолитного хода, обозначим этот угол через aН.
aB—II – дирекционный угол конечной стороны разомкнутого теодолитного хода, обозначим этот угол через aК.
Выразим теоретическую сумму углов в точках А и В.
Угловая невязка разомкнутого теодолитного хода
Если в рассматриваемом ходе не два измеренных угла, а n углов, тогда угловая невязка примет следующее выражение:
Увязка приращений координат в замкнутом
И разомкнутом теодолитных ходах
Приращения координат ΔХ в замкнутом теодолитном ходе – это проекции линий на оси координат Х и У соответственно. Теоретически ΣΔХ = 0 и ΣΔУ = 0. Практически из-за неизбежных ошибок измерений при вычислении ΣΔХ ≠ 0 и ΣΔУ ≠ 0.
Вычисленные ΣΔХ и ΣΔУ называются невязками приращений координат, т. е.
На рис. 66 приводится графическая интерпретация невязок хода.
Абсолютная линейная невязка хода fабс = I–I’ вычисляется по формуле
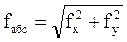
Рис. 66. Невязки в теодолитных ходах
О точности теодолитного хода судят по относительной линейной невязке: 
где Р – сумма длин линий теодолитного хода.
В теодолитных ходах при средних условиях местности допустимая относительная невязка fдоп = 1:2000, а при неблагоприятных – fдоп = 1:1000. Если относительная ошибка fотн > fдоп, то в полевых условиях проверяют измеренные длины линий.
Допустимые невязки fx и fy распределяются на вычисленные приращения координат ΔХ и ΔУ пропорционально длинам сторон и со знаком, противоположным знаку невязки (в табл. 5 колонки 7 и 8).
Например, поправка в приращение, равное +210,32, по оси Х составит
Найдем линейную невязку в разомкнутом теодолитном ходе II–A–B–IV (см. рис. 66). При безошибочном измерении длин линий точки IV и IV’ должны совместиться.
Линейные невязки по осям Х и У:
Если в разомкнутом теодолитном ходе n сторон, и известны координаты начальной ХН и УН и конечной точек ХК и, тогда выражения для линейных невязок по координатным осям принимают следующий вид:
Абсолютная и относительная линейные невязки вычисляются по приведенным выше формулам:
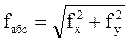

В табл. 5 приведем пример обработки угловых измерений и расчет координат точек замкнутого теодолитного хода.
6.1.7. Построение координатной сетки
при помощи циркуля и линейки
На листе бумаги через ее углы проводят две диагонали 1–1 и 2–2 (рис. 67, а).
Рис. 67. Построение координатной сетки
От точки пересечения диагоналей О откладывают равные отрезки, концы которых соединяют прямыми линиями (см. рис. 67, б). Стороны полученного прямоугольника делят пополам и проводят линии, которые должны пересекать точку О (см. рис. 67,б). От середины каждой стороны откладывают отрезки по 10 см и проводят линии сетки (см. рис. 67, в). Лишние линии убирают (см. рис. 67, г).
На рис. 67, д, е показано получение сетки из 9 квадратов.
Построение плана теодолитной съемки
Координатную сетку оцифровывают с соответствии с координатами вершин теодолитного хода. На оцифрованную сетку наносят точки теодолитного хода по их координатам (рис. 68).
Рис. 68. Построение плана
Нанесение точек рассмотрим на конкретном примере:
ХI = – 168,35, YI = – 40,85 в масштабе плана 1:1000.
Точность поперечного масштаба составляет 0,2 м, поэтому координаты точки I округляем до дециметров и получим
ХI = – 168,4, YI = – 40,8. Определяем квадрат, в котором находится точка I.
По оси Х от метки – 100 по западной и восточной сторонам квадрата в южном направлении откладываем 68,4 м, в масштабе 1:1000 это составит 68,4 мм и проводим линию аb. По оси Y от точки b откладываем 40,8 мм и получаем точку I. Аналогично выполняется нанесение на план остальных точек теодолитного хода II, III, IV, V.
Правильность построения теодолитного хода проверяется по длинам его сторон, а также по дирекционным углам этих сторон, т. е. измеренные длины и углы на плане должны соответствовать длинам и углам на местности.
По данным абриса – схематического чертежа, выполняемого при теодолитной съемке, наносят объекты и контуры.
На рис. 68 показано построение пешеходной тропы 1–2–3, снятой методом полярных координат.
Нанесенные на план объекты и контуры вычерчиваются в принятых условных обозначениях после проверки плана в поле. Некоторые условные обозначения показаны на рис. 69.
 | Точка теодолитного хода |  | Фруктовый сад |
 | Луг |  | Сплошной деревянный забор |
 | Редкий лес |  | ЛЭП низкого напряжения |
 | Строящаяся дорога с покрытием | Рис. 69. Условные знаки для топографических планов масштаба 1:1000 |
Тахеометрическая съемка
Общие сведения
Тахеометрическая съемка – это такой вид съемки, при котором изображаются контуры, местные предметы и рельеф местности.
При этой съемке используются теодолит-тахеометр со штативом и отвесом (Т30, 2Т30, 2Т30М и др.) и нивелирная рейка РН‑4.
Геодезической основой съемки служат теодолитно-нивелирные (масштаб съемки 1:500) или теодолитно-тахеометрические ходы (масштаб съемки 1:1000–1:5000). Эти ходы могут быть замкнутыми или разомкнутыми в зависимости от снимаемой территории.
В теодолитно-нивелирных ходах (ТНХ) и в теодолитно-тахеометрических ходах (ТТХ) должны быть известны координаты Х (абсцисса), Y (ордината) и Н (высота) всех вершин полигона.
В ТНХ и ТТХ координаты X и Y получают по данным обработки угловых и линейных измерений теодолитного хода.
Координаты Н точек в ТНХ находят по данным геометрического нивелирования. В ТТХ высоты Н точек вычисляют по результатам тригонометрического нивелирования.