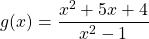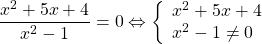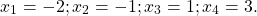Что называется нулем функции
Нуль функции
Нуль функции в математике — элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции 
, заданной формулой
является нулём, поскольку
.
Нули функции также называются корнями функции.
Понятие нулей функции можно рассматривать для любых функций, область значений которых содержит нуль или нулевой элемент соответствующей алгебраической структуры.
Для функции действительного переменного 
нулями являются значения, в которых график функции пересекает ось абсцисс.
Нахождение нулей функции часто требует использования численных методов (к примеру, метод Ньютона, градиентные методы).
Одной из нерешённых математических проблем является нахождение нулей дзета-функции Римана.
Корень многочлена
Основная теорема алгебры утверждает, что каждый многочлен степени n имеет n комплексных корней, учитывая их кратность. Комплексные корни всегда входят сопряжёнными парами. Каждый многочлен нечётной степени имеет по крайней мере один действительный корень. Связь между корнями многочлена и его коэффициентами устанавливает теорема Виета.
См. также
Литература
Полезное
Смотреть что такое «Нуль функции» в других словарях:
Нуль функции — точка, где заданная функция f (z) обращается в нуль; таким образом, Н. ф. f (z) это то же самое, что и корни уравнения f (z) = 0. Например, точки 0, π, π, 2π, 2π. суть нули функции sinz. Нули аналитической функции (См. Аналитические… … Большая советская энциклопедия
нуль-функция — нуль функция, нуль функции … Орфографический словарь-справочник
Нуль (комплексный анализ) — У этого термина существуют и другие значения, см. Нуль. Необходимо перенести содержимое этой статьи в статью «Нуль функции». Вы можете помочь проекту, объединив статьи. В случае необходимости обсуждения целесообразности объединения, замените этот … Википедия
НУЛЬ-ЗАРЯД — в квантовой теории поля принятое (жаргонное) название для свойства обращения в нуль фактора перенормировки константысвязи где g0 затравочная константа связи из лагранжиана взаимодействия, физ. константа связи, одетая взаимодействием. Равенство Z … Физическая энциклопедия
Нуль-мутация н-аллель — Нуль мутация, н. аллель * нуль мутацыя, н. алель * null mutation or n. allel or silent a. мутация, ведущая к полной потере функции в той последовательности ДНК, в которой она произошла … Генетика. Энциклопедический словарь
НУЛЬ — 1) Число, обладающее тем свойством, что любое (действительное или комплексное) число при сложении с ним не меняется. Обозначается символом 0. Произведение любого числа на Н. равно Н.: Если произведение двух чисел равно Н., то один из сомножителей … Математическая энциклопедия
Неявные функции — функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение x2 + y2 1 = 0 задаёт Н. ф. … Большая советская энциклопедия
Нуль функции
Смотреть что такое «Нуль функции» в других словарях:
Нуль функции — Нули косинуса на интервале [ 2π,2π] (красные точки) Нуль функции в математике элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции … Википедия
нуль-функция — нуль функция, нуль функции … Орфографический словарь-справочник
Нуль (комплексный анализ) — У этого термина существуют и другие значения, см. Нуль. Необходимо перенести содержимое этой статьи в статью «Нуль функции». Вы можете помочь проекту, объединив статьи. В случае необходимости обсуждения целесообразности объединения, замените этот … Википедия
НУЛЬ-ЗАРЯД — в квантовой теории поля принятое (жаргонное) название для свойства обращения в нуль фактора перенормировки константысвязи где g0 затравочная константа связи из лагранжиана взаимодействия, физ. константа связи, одетая взаимодействием. Равенство Z … Физическая энциклопедия
Нуль-мутация н-аллель — Нуль мутация, н. аллель * нуль мутацыя, н. алель * null mutation or n. allel or silent a. мутация, ведущая к полной потере функции в той последовательности ДНК, в которой она произошла … Генетика. Энциклопедический словарь
НУЛЬ — 1) Число, обладающее тем свойством, что любое (действительное или комплексное) число при сложении с ним не меняется. Обозначается символом 0. Произведение любого числа на Н. равно Н.: Если произведение двух чисел равно Н., то один из сомножителей … Математическая энциклопедия
Неявные функции — функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение x2 + y2 1 = 0 задаёт Н. ф. … Большая советская энциклопедия
Нули функции
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
1) Найти нули линейной функции y=3x+15.
Чтобы найти нули функции, решим уравнение 3x+15 =0.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Для нахождения нулей функции решим квадратное уравнение
Его корни x1=3 и x2=4 являются нулями данной функции.
3)Найти нули функции
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
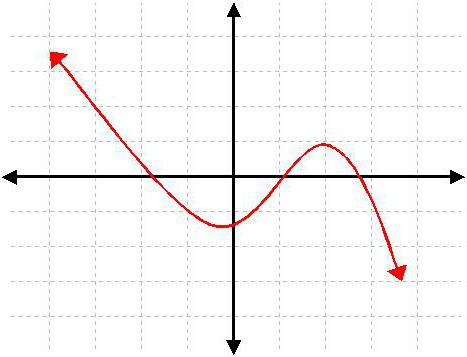
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
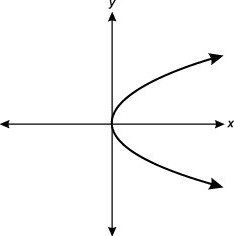
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Что называется нулями функции
Нуль функции в математике — элемент из области определения функции, в котором она принимает нулевое значение. Например, для функции f 
, заданной формулой
Понятие нулей функции можно рассматривать для любых функций, область значений которых содержит нуль или нулевой элемент соответствующей алгебраической структуры.
Для функции действительного переменного f : R → R o mathbb > нулями являются значения, в которых график функции пересекает ось абсцисс.
Нахождение нулей функции часто требует использования численных методов (к примеру, метод Ньютона, градиентные методы).
Одной из нерешённых математических проблем является нахождение нулей дзета-функции Римана.
Корень многочлена [ править | править код ]
Основная теорема алгебры утверждает, что каждый многочлен степени n имеет n комплексных корней, учитывая их кратность. Комплексные корни всегда входят сопряжёнными парами. Каждый многочлен нечётной степени имеет по крайней мере один действительный корень. Связь между корнями многочлена и его коэффициентами устанавливает теорема Виета.
Комплексный анализ [ править | править код ]
Простой нуль аналитической в некоторой области G ⊂ C > функции f — точка z 0 ∈ G in G> , в некоторой окрестности которой справедливо представление f ( z ) = ( z − z 0 ) g ( z ) )g(z)> , где g аналитична в z 0 > и не обращается в этой точке в нуль.
Нуль порядка k аналитической в некоторой области G ⊂ C > функции f — точка z 0 ∈ G in G> , в некоторой окрестности которой справедливо представление f ( z ) = ( z − z 0 ) k g ( z ) )^ g(z)> , где g аналитична в z 0 > и не обращается в этой точке в нуль.
Нули аналитической функции изолированы.
Другие специфические свойства нулей комплексных функций выражаются в различных теоремах:
Что такое нули функции? Ответит довольно прост – это математический термин, под которым подразумевают область определения заданной функции, на котором ее значение нулевое. Нули функции также называют корнями уравнения. Проще всего пояснить, что такое нули функции, на нескольких простых примерах.
Примеры
Рассмотрим несложное уравнение у=х+3. Поскольку нуль функции – это значение аргумента, при котором у приобрел нулевое значение, подставим 0 в левую часть уравнения:
Рассмотрим другой пример:
Подставим 0 в левую часть уравнения, как и в предыдущем примере:
Алгоритм определения
Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:
Сложность последнего пункта зависит от степени аргумента уравнения. При решении уравнений высоких степеней особенно важно помнить, что количество корней уравнения равно максимальной степени аргумента. Особенно это актуально для тригонометрических уравнений, где деление обоих частей на синус или косинус приводит к потере корней.
Уравнения произвольной степени проще всего решать методом Горнера, который был разработан специально для нахождения нулей произвольного многочлена.
Значение нулей функций может быть как отрицательным, так и положительным, действительным или лежащим в комплексной плоскости, единичным или множественным. Или же корней уравнения может и не быть. Например, функция у=8 не приобретет нулевого значения ни при каком х, потому что она не зависит от этой переменной.
Типичные ошибки
Частая ошибка, которую допускают школьники, еще не разобравшиеся толком в том, что такое нули функции, – это замена на ноль аргумента (х), а не значения (у) функции. Они уверенно подставляют в уравнение х=0 и, исходя из этого, находят у. Но это неправильный подход.
Другая ошибка, как уже упоминалось, сокращение на синус или косинус в тригонометрическом уравнении, из-за чего и теряется один или несколько нулей функции. Это не означает, что в таких уравнениях нельзя ничего сокращать, просто при дальнейших подсчетах необходимо учитывать эти «потерянные» сомножители.
Графическое представление
Понять, что такое нули функции, можно с помощью математических программ, таких как Maple. В ней можно построить график, указав желаемое количество точек и нужный масштаб. Те точки, в которых график пересечет ось ОХ, и есть искомые нули. Это один из самых быстрых способов нахождения корней многочлена, особенно если его порядок выше третьего. Так что если есть необходимость регулярно выполнять математические расчеты, находить корни многочленов произвольных степеней, строить графики, Maple или аналогичная программа будет просто незаменима для осуществления и проверки расчетов.
Необходимое и достаточное условия нуля порядка n