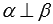Что называется наклонной на плоскости

Перпендикуляр и наклонная. Расстояние от прямой до плоскости

Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

Пер­вый спо­соб.

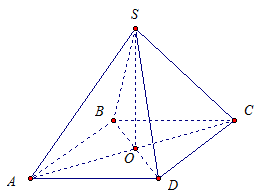
Имеем квад­рат, центр квад­ра­та точка – О, SО – пер­пен­ди­ку­ляр. Зна­чит, для на­клон­ной SC от­ре­зок ОС есть про­ек­ция.

Пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой ОС, ко­то­рая яв­ля­ет­ся про­ек­ци­ей на­клон­ной SC, зна­чит, по тео­ре­ме о трех пер­пен­ди­ку­ля­рах, пря­мая ВD пер­пен­ди­ку­ляр­на на­клон­ной SC.

Вто­рой спо­соб.

Пря­мая SО пер­пен­ди­ку­ляр­на плос­ко­сти АВС, а зна­чит – и пря­мой ВD, ле­жа­щей в ней.

Пря­мая ВD пер­пен­ди­ку­ляр­на SО и пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой АС по свой­ству квад­ра­та.

По­лу­ча­ем, что пря­мая ВD пер­пен­ди­ку­ляр­на двум пе­ре­се­ка­ю­щим­ся пря­мым плос­ко­сти SОС, зна­чит, она пер­пен­ди­ку­ляр­на ко всей плос­ко­сти SОС, а зна­чит – и к пря­мой SC, ле­жа­щей в этой плос­ко­сти.

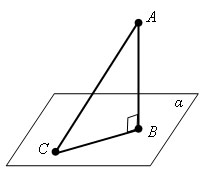
Расстояние от точки до плоскости есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ.

В единичном тетраэдре DABC найдите расстояние от точки C до плоскости ADB.

Основанием прямого параллелепипеда служит параллелограмм с углом 120 \(^\circ\) и сторонами, равными 3 и 4. Меньшая диагональ параллелепипеда равна большей диагонали основания. Найдите объем параллелепипеда.

Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.

Через вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная его плоскости. Расстояния от точки К до других вершин прямоугольника равны 12 м, 14 м, 18 м. Найдите отрезок АК.

Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС.

АВ = АС = 10 см, ВС = 12 см, AD = 6 см.

Найдите расстояние от точки D до ВС.

Через вершину прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскости прямоугольника.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №10. Перпендикуляр и наклонные

Перечень вопросов, рассматриваемых в теме.

Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения

Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.

Источник

Перпендикуляр и наклонная

Определение. Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости.

Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, не являющийся перпендикуляром к плоскости, с одним концом в данной точке, а с другим – на плоскости.

Конец отрезка, лежащий в плоскости, называется основанием наклонной.

Отрезок, соединяющий основание перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной (рис.24)

СВ – проекция наклонной

С – основание наклонной,

В – основание перпендикуляра

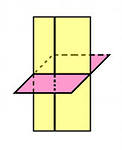
Определение. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен девяноста градусам (рис.26)

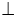
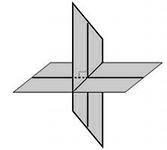
Для обозначения перпендикулярности используют символ вида « ». То есть, если плоскости α и β перпендикулярны, то можно кратко записать

Определение. Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым (рис.27)

Если плоскости α и β перпендикулярны, то можно также сказать, что плоскость α перпендикулярна к плоскости β или плоскость β перпендикулярна к плоскости α. Поэтому перпендикулярные плоскости α и β часто называют взаимно перпендикулярными.

В качестве примера перпендикулярных плоскостей можно привести плоскости стены и пола в комнате.

Также существует признак перпендикулярности двух плоскостей, который часто используется для доказательства перпендикулярности двух плоскостей. В его формулировке участвуют перпендикулярные прямая и плоскость.

Источник

Определение перпендикуляра и наклонной

1) Определение перпендикуляра и наклонной.

Пусть дана плоскость и не лежащая на ней точка.

· Отрезок прямой, перпендикулярной плоскости, соединяющий данную точку с точкой на плоскости называется перпендикуляром из данной точки к данной плоскости.

· Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

· Любой отрезок, соединяющий данную точку с точкой на плоскости и не являющийся перпендикуляром к плоскости, называется наклонной.

· Конец отрезка, лежащий в плоскости, называется основанием наклонной.

2) Доказательство того, что перпендикуляр корочек наклонной

На рисунке 2 изображена плоскость α, перпендикуляр к ней AO, наклонная AB, а также показан отрезок BO, соединяющий основания наклонной и перпендикуляра. Отрезки AO, BO и AB образуют ΔAOB.

Рассмотрим ΔAOB, из определения перпендикуляра следует, что он прямоугольный. Перпендикуляр AO является катетом этого треугольника, а наклонная AB – его гипотенузой. Катет прямоугольного треугольника всегда меньше его гипотенузы (по теореме Пифагора), следовательно, перпендикуляр всегда короче наклонной.

3) Определение проекции

Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

Отрезок BO на рисунке 2 – является проекцией наклонной AB.

4) Теорема о сравнительной длине наклонных и их проекций

А) Любая наклонная больше своей проекции.

Вновь рассмотрим ΔAOB, изображенный на рис. 2, из определения перпендикуляра следует, что он прямоугольный. Проекция BO является катетом этого треугольника, а наклонная AB – его гипотенузой, т. к. катет прямоугольного треугольника всегда меньше его гипотенузы, следовательно, проекция наклонной на плоскость всегда короче самой наклонной.

Б) Равные наклонные имеют равные проекции

Доказательство: Рассмотрим треугольники AOB и AOD, они равны, т. к. равны их гипотенузы AB и AD, и углы AOB и AOD (они прямые), а сторона AO у них общая. Из равенства треугольников следует и равенство их сторон BO = OD, что и требовалось доказать.

В) Если проекции наклонных равны, то и наклонные равны. Доказывается аналогично утверждению Б.

Г) Большей наклонной соответствует большая проекция.

Рассмотрим прямоугольные треугольники AOB и AOD, AB > AD.

=

=

Но так как AB > AD => AB2 > AD2 => > =>

=> BO > DO. Что и требовалось доказать.

Д) Из двух наклонных больше та, у которой проекция больше. Доказывается аналогично Г.

Источник

Перпендикуляр к плоскости. Наклонная

Поставим задачу определить, в каком случае прямая может считаться перпендикулярной к плоскости. Докажем предварительно следующее предложение.

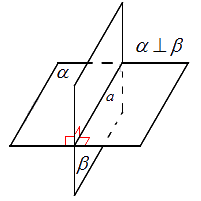
Теорема. Если прямая (АА₁, черт. 15), пересекающаяся с плоскостью (МN), перпендикулярна к каким-нибудь двум прямым (ОВ и ОС), проведенным на этой плоскости через точку пересечения (O) данной прямой и плоскости, то она перпендикулярна и ко всякой третьей прямой (ОD), проведённой на плоскости через ту же точку пересечения (О).

Отложим на прямой АА₁ произвольной длины, но равные отрезки ОА и ОА₁ и проведём на плоскости какую-нибудь прямую, которая пересекала бы три прямые, исходящие из точки О, в каких-нибудь точках С, D и В. Эти точки соединим с точками А и А₁. Мы получим тогда несколько треугольников. Рассмотрим их в такой последовательности.

Сначала возьмём треугольники АСВ и А₁СВ; они равны, так как у них СВ—общая сторона, АС=А₁С, как наклонные к прямой АА₁, одинаково удалённые от основания О перпендикуляра ОС; по той же причине АВ = А₁В. Из равенства этих треугольников следует, что ∠ АВС = ∠ А₁BС.

После этого перейдём к треугольникам АОВ и А₁ОВ; они равны, так как у них ОВ—общая сторона, АВ = А₁В и ∠АВD = ∠А₁ВD. Из равенства этих треугольников выводим, что АО = А₁О.

Определение. Прямая называется перпендикулярной к плоскости, если она, пересекаясь с этой плоскостью, образует прямой угол с каждой прямой, проведённой на плоскости через точку пересечения. В этом случае говорят также, что плоскость перпендикулярна к прямой.

Из предыдущей теоремы следует, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым, лежащим в данной плоскости и проходящим через точку пересечении данной прямой и плоскости.

Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости. Точка пересечения прямой с плоскостью называется основанием перпендикуляра или наклонной.

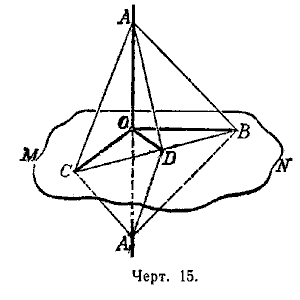
Сравнительная длина перпендикуляра и наклонных. Когда из одной точки А (черт. 16) проведены к плоскости перпендикуляр АВ и наклонная АС, условимся называть, проекцией наклонной на плоскость Р отрезок ВС, соединяющий основание перпендикуляра и основание наклонной.

Для краткости термины «перпендикуляр» и «наклонная» употребляются вместо «отрезок перпендикуляра, ограниченный данной точкой и основанием перпендикуляра», и «отрезок наклонной, ограниченный данной точкой и основанием наклонной.

Таким образом, отрезок ВС есть проекция наклонной АС, отрезок ВD есть проекция наклонной АD и т. д.

1) две наклонные, имеющие равные проекции, равны;

2) из двух наклонных та больше, проекция которой больше,

Вращая прямоугольные треугольники ABC и ABD вокруг катета AB, мы можем совместить их плоскости с плоскостью \(\Delta\)ABE. Тогда все наклонные будут лежать в одной плоскости с перпендикуляром, а все проекции расположатся на одной прямой. Таким образом, доказываемые теоремы приводятся к аналогичным теоремам планиметрии.

Обратные теоремы. Если из одной и той же точки, взятой вне плоскости, проведены перпендикуляр и какие-нибудь наклонные, то:

1) равные наклонные имеют равные проекции;

2) из двух проекций та больше, которая соответствует большей наклонной.

Приведём ещё следующую теорему о перпендикулярах, которая понадобится нам впоследствии.

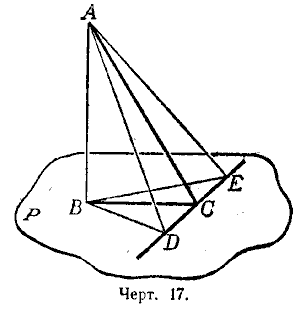
Теорема. Прямая (DЕ, черт. 17), проведённая на плоскости (Р) через основание наклонной (АС) перпендикулярно к её проекции (ВС), перпендикулярна и к самой наклонной.

Отложим произвольные, но равные отрезки СD и СЕ и соединим прямолинейными отрезками точки А и В с точками D и E. Тогда будем иметь:

ВD = ВЕ, как наклонные к прямой DЕ, одинаково удалённые от основания С перпендикуляра ВС;

АD = АЕ, как наклонные к плоскости Р, имеющие равные проекции ВD и ВЕ.

Вследствие этого \(\Delta\)АDЕ равнобедренный, и потому его медиана АС перпендикулярна к основанию DЕ.

Эта теорема носит название теоремы о трёх перпендикулярах. Действительно, в ней говорится о связи, соединяющей следующие три перпендикуляра:

1) АВ к плоскости Р,

2) ВС к прямой DE и

3) АС к той же прямой DE.

Обратная теорема. Прямая (ОЕ, черт. 17), проведённая на плоскости (Р) через основание наклонной (АС) перпендикулярно к этой наклонной, перпендикулярна и к её проекции.

Сделаем те же построения, что и при доказательстве прямой теоремы. Отложим произвольные, но равные отрезки СD и СЕ и соединим прямолинейными отрезками точки А и В с точками D и Е, тогда будем иметь:

АD = АЕ, как наклонные к прямой DЕ, одинаково удалённые от основания С перпендикуляра АС;

ВD = ВЕ, как проекции равных наклонных АD и АЕ.

Вследствие этого \(\Delta\)ВDЕ равнобедренный, и потому его медиана ВС перпендикулярна к основанию DЕ.

Источник