Что называется мнимой единицей

Мнимая единица – число на грани мистики

Человеку не сведущим в математике и физике рассуждения о мнимой единице представляется полным бредом. Например, квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Отсюда ясно, что квадратные корни из отрицательных чисел не могут находиться среди возможных действительных чисел. Следовательно, нам не остается ничего другого, как признать их невозможными числами.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел. Это было сделано китайскими математиками во II веке до н. э. Отрицательные числа не так просты. Представьте, сколько будет 3 – 4? Как можно отнять 4 барана от 3? Отрицательные числа рассматривались как полная чушь. Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число Е и много еще чего, не понимал отрицательные числа так же хорошо, как

мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений. Древнегреческие математики считали «настоящими» только натуральные числа.

То, что называют мнимым числом, на самом деле частный случай комплексного числа. Это число настоящим числом назвать нельзя. Учебники описывают его как величину, которая, будучи возведенной в квадрат, дает минус один. Другими словами, это сторона квадрата с отрицательной площадью. В реальности такого не бывает. Впервые понятие «мнимая величина» использовал Кардано (1545). Он решал задачу с помощью квадратных уравнений

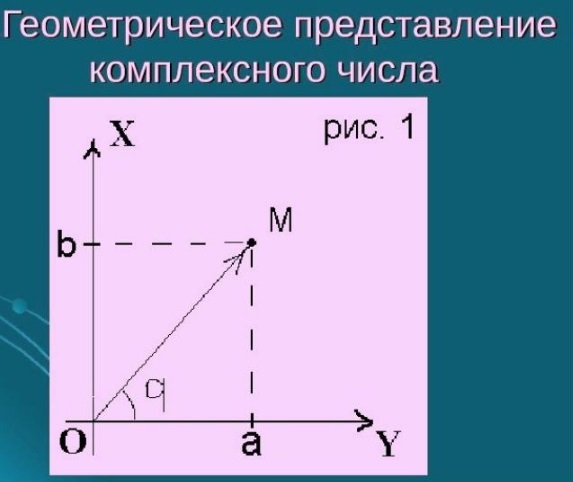
Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс означает связь, сочетание, совокупность понятий, предметов, явлений образующих единое целое. В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изобразить комплексное число z = a + b × i точкой m (a, b) на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M, а вектором, идущим в эту точку из начала координат. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. В дальнейшем Леонард Эйлер (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) получил знаменитую формулу, и открыл комплексным числам дорогу в самые различные области математики и ее приложений.

Комплексные числа – расширили понятие числа. В 1843 году ирландский математик Уильям Гамильтон предложил четырехмерную систему комплексных чисел, которая стала первой гиперкомплексной системой, названную кватернионами. Теория кватернионов вскоре стала одним из источников дальнейшего развития математики и ее приложений.

Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения.

Источник

Лекция по высшей математике «Мнимая единица. Алгебраическая форма комплексного числа»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Алгебраическая форма комплексного числа.

Цели: расширить понятие числа, ввести понятие мнимой единицы и ее степеней, понятие комплексного числа; рассмотреть алгебраическую форму комплексного числа ; развивать умения обобщать полученные знания, способствовать развитию логического мышления;

воспитывать у обучающихся сознательное отношение к процессу обучения.

Мнимые числа. Определение мнимой единицы. Степени мнимой единицы.

Определение комплексного числа.

Алгебраическая форма комплексного числа.

Например:

Например: и и .

Теорема. Люб ая натуральн ая степень числа і может быть преобразован а к

Пусть m =4 k +3, тогда і м

Пример. Вычислить значение выражения

.

Замечание. Для того, чтобы вычислить степень мнимой единицы, удобно пользоваться таким правилом:

1) разделить показатель степени на 4;

Символически действительную и мнимую части комплексного числа обозначают так: (ре зет), (им зет).

Замечание. Иногда мнимой частью комплексного числа z = а + b і называют bi.

Для комплексных чисел не существует понятий больше и меньше, то есть комплексные числа не сравнимы.

Определение. Комплексное число (-а- bi ) называется противоположным комплексному числу

Определение. Два комплексных числа, у которых действительные части равны, а мнимые

части противоположные, называются комплексно сопряженными числами и

обозначаются соответственно и .

3.Алгебраическая форма комплексного числа. Действия над комплексными числами, заданными в алгебраической форме.

Сложение комплексных чисел

Определение. Суммой двух комплексных чисел и называется

комплексное число .

Итак, (1)

Таким образом, чтобы сложить два комплексных числа нужно сложить их действительные части, и это дает действительную часть суммы, и сложить мнимые части, что дает мнимую часть суммы.

Сумма сопряженных чисел всегда является действительн ым числом

то есть, . (2)

Вычитание комплексных чисел

Определение. Разностью двух комплексных чисел и называется такое

комплексное число , которое в сумме с числом дает число .

Вычитание комплексных чисел всегда возможно.

Теорема. Для любых комплексных чисел и всегда существует разница , которая определена однозначно.

Таким образом, для того, чтобы вычесть комплексные числа, достаточно вычесть их действительные части и их разницу взять за действительную часть разности, а также вычесть мнимую часть разности

Получается, (3)

Разность двух сопряженных чисел всегда является мнимым числом. ,

то есть, (4)

Умножение комплексных чисел

Определение. Произведением двух комплексных чисел и называется такое комплексное число, которое определяется формулой: (5)

В процессе умножения комплексных чисел лучше выполнять непосредственное умножение. Произведение сопряженных чисел всегда является действительным числом

.

Пример. Найти значение выражения .

Решение: .

Деление комплексных чисел

Определение. Частным двух комплексных чисел и называется такое

комплексное число z, которое в произведении с дает .

Всегда существует частное от деления двух комплексных чисел, если знаменатель отличается от нуля.

Теорема. Частное определено и к тому же однозначно для всех комплексных чисел и , если только , то есть .

(7)

Пример. Вычислить значение выражения .

Решение:

Над комплексными числами в алгебраической форме возможно выполнять и такие действия, как возведение в степень, извлечения корня. Но выполнение этих действий в алгебраической форме довольно трудоемкое.

Закрепление изученного материала.

1. Вычислить:

2. Среди приведенных примеров укажите :

а) чисто мнимые комплексные числа;

б) чисто действительные комплексные числа;

в) сопряженные комплексные числа;

г) равные комплексные числа:

3. Выполнить действия: Ответ.

4. На основании равенства комплексных чисел найти действи­тельные числа и если Ответ.

5. Решить квадратные уравнения и проверить выполнение тео­ремы Виета:

а) б) Ответ. а) б)

1.Дать определение комплексного числа.

2.Сформулировать определение мнимой единицы.

3.Как найти степень мнимой единицы.

4.Какие комплексные числа называют равными, сопряженными?

5.Записать формулу для нахождения произвольного степени мнимой единицы.

6. Приведите примеры чисто мнимых чисел.

7. Дать определение суммы, произведения и частного двух комплексных чисел.

Письменный, Д. Т. Конспект лекций по высшей математике: полный курс Д. Т. Письменный. – 9-е изд. – М.: Айрис-пресс, 2009. 608 с.: ил. – (Высшее образование).

Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 7-е изд. – М.: Айрис-пресс, 2008. 576 с.: – (Высшее образование).

Григорьев В. П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования / В. П. Григорьев, Ю. А. Дубинский. – 10-е изд., стер. – М. Издательский центр «Академия», 2014. – 320 с.

Источник

СОДЕРЖАНИЕ

Определение

Мнимое число i определяется исключительно тем свойством, что его квадрат равен −1:

.>

Точно так же, как и с любым ненулевым действительным числом:

Матрицы

Аналогичная проблема возникает, если комплексные числа интерпретируются как вещественные матрицы 2 × 2 (см. Матричное представление комплексных чисел ), потому что тогда оба

были бы решениями матричного уравнения

Все эти неоднозначности могут быть решены путем принятия более строгого определения комплексного числа и явным выбором одного из решений уравнения в качестве мнимой единицы. Например, упорядоченная пара (0, 1) в обычном построении комплексных чисел с двумерными векторами.

Правильное использование

а ⋅ б знак равно а ⋅ б <\ displaystyle <\ sqrt > \ cdot <\ sqrt > = <\ sqrt >>

а б знак равно а б <\ displaystyle <\ frac <\ sqrt > <\ sqrt >> = <\ sqrt <<\ frac <\, a \,>> \,>>>

Источник

Мнимая единица

Мни́мая едини́ца — обычно комплексное число, квадрат которого равен −1 (минус единице). Однако возможны и иные варианты: в конструкции удвоения по Кэли—Диксону или в рамках алгебры по Клиффорду.

Содержание

Для комплексных чисел

Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f(x)=0 с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x^2 + 1 = 0 не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».

Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.

Утверждение, что мнимая единица — это «квадратный корень из −1», не точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i через радикал (как \sqrt <-1>).

Определение

Мнимая единица — это число, квадрат которого равен −1. Т.е. i — это одно из решений уравнения

Степени мнимой единицы

Степени i повторяются в цикле:

Что может быть записано для любой степени в виде:

где n — любое целое число.

Факториал

Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i :

Корни из мнимой единицы

В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.

Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:

Также корни из мнимой единицы могут быть представлены в показательном виде:

Иные мнимые единицы

К вопросу об интерпретации и названии

Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i.

Обозначения

См.также

Напишите отзыв о статье «Мнимая единица»

Примечания

Ссылки

Отрывок, характеризующий Мнимая единица

В самом городе между тем было пусто. По улицам никого почти не было. Ворота и лавки все были заперты; кое где около кабаков слышались одинокие крики или пьяное пенье. Никто не ездил по улицам, и редко слышались шаги пешеходов. На Поварской было совершенно тихо и пустынно. На огромном дворе дома Ростовых валялись объедки сена, помет съехавшего обоза и не было видно ни одного человека. В оставшемся со всем своим добром доме Ростовых два человека были в большой гостиной. Это были дворник Игнат и казачок Мишка, внук Васильича, оставшийся в Москве с дедом. Мишка, открыв клавикорды, играл на них одним пальцем. Дворник, подбоченившись и радостно улыбаясь, стоял пред большим зеркалом.
– Вот ловко то! А? Дядюшка Игнат! – говорил мальчик, вдруг начиная хлопать обеими руками по клавишам.
– Ишь ты! – отвечал Игнат, дивуясь на то, как все более и более улыбалось его лицо в зеркале.
– Бессовестные! Право, бессовестные! – заговорил сзади их голос тихо вошедшей Мавры Кузминишны. – Эка, толсторожий, зубы то скалит. На это вас взять! Там все не прибрано, Васильич с ног сбился. Дай срок!
Игнат, поправляя поясок, перестав улыбаться и покорно опустив глаза, пошел вон из комнаты.
– Тетенька, я полегоньку, – сказал мальчик.
– Я те дам полегоньку. Постреленок! – крикнула Мавра Кузминишна, замахиваясь на него рукой. – Иди деду самовар ставь.
Мавра Кузминишна, смахнув пыль, закрыла клавикорды и, тяжело вздохнув, вышла из гостиной и заперла входную дверь.
Выйдя на двор, Мавра Кузминишна задумалась о том, куда ей идти теперь: пить ли чай к Васильичу во флигель или в кладовую прибрать то, что еще не было прибрано?
В тихой улице послышались быстрые шаги. Шаги остановились у калитки; щеколда стала стучать под рукой, старавшейся отпереть ее.
Мавра Кузминишна подошла к калитке.
– Кого надо?
– Графа, графа Илью Андреича Ростова.
– Да вы кто?
– Я офицер. Мне бы видеть нужно, – сказал русский приятный и барский голос.
Мавра Кузминишна отперла калитку. И на двор вошел лет восемнадцати круглолицый офицер, типом лица похожий на Ростовых.
– Уехали, батюшка. Вчерашнего числа в вечерни изволили уехать, – ласково сказала Мавра Кузмипишна.
Молодой офицер, стоя в калитке, как бы в нерешительности войти или не войти ему, пощелкал языком.
– Ах, какая досада. – проговорил он. – Мне бы вчера… Ах, как жалко.
Мавра Кузминишна между тем внимательно и сочувственно разглядывала знакомые ей черты ростовской породы в лице молодого человека, и изорванную шинель, и стоптанные сапоги, которые были на нем.
– Вам зачем же графа надо было? – спросила она.
– Да уж… что делать! – с досадой проговорил офицер и взялся за калитку, как бы намереваясь уйти. Он опять остановился в нерешительности.
– Видите ли? – вдруг сказал он. – Я родственник графу, и он всегда очень добр был ко мне. Так вот, видите ли (он с доброй и веселой улыбкой посмотрел на свой плащ и сапоги), и обносился, и денег ничего нет; так я хотел попросить графа…
Мавра Кузминишна не дала договорить ему.

Источник