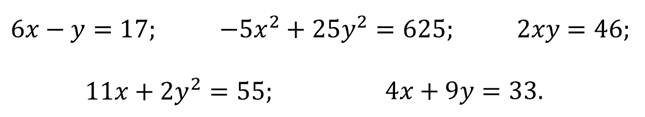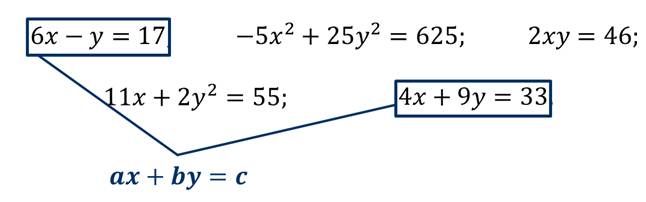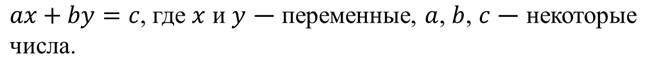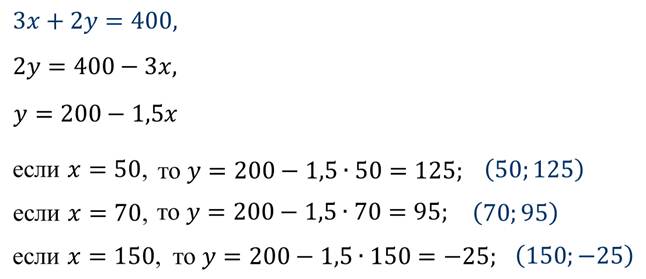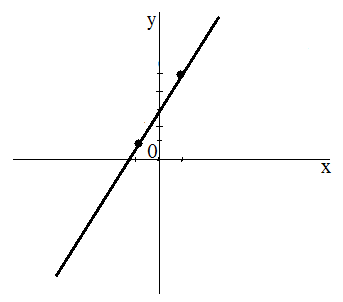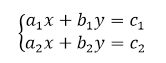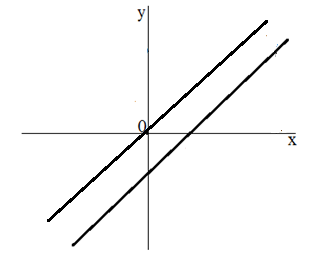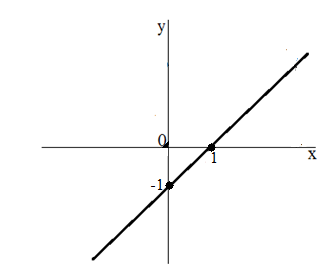Что называется линейным уравнением с двумя переменными

Линейные уравнения с двумя переменными

Линейные уравнения с двумя переменными

Определение: Решение уравнения с двумя переменными – это пара значений переменных, обращающая это уравнение в верное равенство.

т. е. пара чисел (4; 1,5) не является решением уравнения.

Определение: Равносильные уравнения – это уравнения, имеющие одни и те же решения или не имеющие их.

1. В уравнении можно перенести слагаемое из одной части уравнения в другую, изменив его знак.

2. Обе части уравнения можно множить или разделить на одно и то же отличное от нуля число.

Выразить одну переменную через другую:

1) 2х +у = 5 2) 3)

График линейного уравнения с двумя переменными

Определение: График уравнения с двумя переменными – это множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

1. Пример: 3х + 2у = 6, где а=3, b=2, c=6

План 1) Выразить переменную у

у =

2) Составить таблицу значений х и у

3) Построить график

2. Частные случаи построения графика ax + by = c

у =

x =

х = 2

Графика не существует

График – вся координатная плоскость

Решение систем уравнений с двумя переменными. Графический способ.

Определение: Система уравнений – это несколько уравнений, для которых находят общее решение.

Определение: Решение системы уравнений с двумя переменными – это пара значений переменных, обращающая каждое уравнение в верное равенство.

Если х=7, у=5, то , , верно,

т. е. (7; 5) – решение системы уравнений.

Определение: Решить систему – это значит найти все ее решения или доказать, что решений нет.

План решения системы уравнений графическим способом

1. Выразить переменную у в первом уравнении.

2. Выразить переменную у во втором уравнении.

3. В одной системе построить графики данных функций.

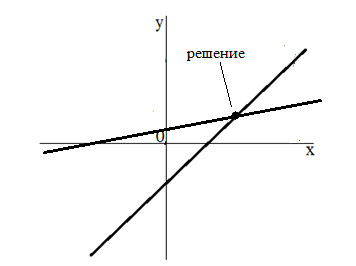
4. Координаты точки пересечения графиков и является решением системы уравнений.

Пример:

Источник

Линейное уравнение с двумя переменными

Урок 39. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Линейное уравнение с двумя переменными»

· повторить что такое линейное уравнение с одной переменной и сколько решений может иметь такое уравнение;

· ввести понятия «линейное уравнение с двумя переменными», «решение уравнения с двумя переменными», «равносильные уравнения».

Ранее мы с вами рассматривали линейное уравнение с одной переменной.

Сегодня на уроке мы познакомимся с линейным уравнением, но уже с двумя неизвестными.

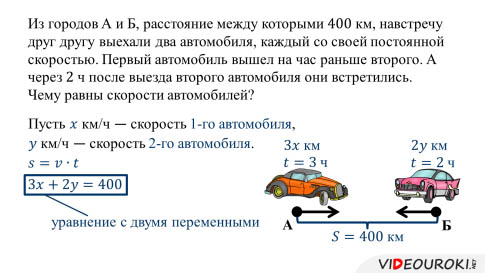
Давайте рассмотрим ситуацию

Полученное равенство содержит две переменные. А поэтому такие равенства называют уравнениями с двумя переменными (или с двумя неизвестными).

Посмотрите на примеры уравнений с двумя переменными

Линейным уравнением с двумя переменными называется уравнение вида:

То есть пара значений переменных (x = 60, y = 110) является решением этого уравнения. Отметим, что эти корни были найдены методом подбора, причём это не единственная пара чисел, удовлетворяющих нашему уравнению.

Решением уравнения с двумя переменными называется пара значений переменных, которая обращает это уравнение в верное равенство.

Вспомним, что при изучении уравнений с одной переменной, мы говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

Аналогично можем сказать, что уравнения с двумя переменными, имеющие одни и те же решения, называются равносильными.

Причем уравнения с двумя переменными, не имеющие решений, также являются равносильными.

Равносильные уравнения обладают следующими свойствами:

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнения, равносильное данному;

Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Снова вернёмся к нашему уравнению

Но здесь важно знать, значение какой из переменных стоит на первом месте, а какой – на втором. Так в нашем случае сначала записано значение переменной x, а затем переменной y.

И давайте рассмотрим ещё одну задачу.

Решение уравнений в целых числах, то есть когда надо найти только целые значения переменных, подробно рассматривал древнегреческий математик Диофант.

Поэтому уравнения с несколькими переменными, которые надо решить в целых числах, называют диофантовыми уравнениями. То есть уравнение, составленное в предыдущей задаче, является диофантовым, так как для него мы отыскивали только натуральные решения.

И давайте рассмотрим примеры.

Итак, на этом уроке мы рассмотрели линейное уравнение с двумя переменными и один из способов решения таких уравнений.

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №42. Линейные уравнения и неравенства с двумя переменными

Перечень вопросов, рассматриваемых в теме:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Уравнения, а также системы уравнений имеют давнюю историю. Нам известно, что уже в Древнем Вавилоне и Индии повседневные задачи, связанные с земляными работами или планированием военных расходов, а также астрономическими наблюдениями решались с помощью уравнений и их систем.

В то время еще не существовало привычного нам формального языка математики. Вавилоняне, также, как и индусы не использовали в своих трактатах привычные нам «икс» и «игрек». Не обозначали степень надстрочными индексами. И т.д. Их уравнения записаны в виде текстовых задач. Также, как и решения, не похожи на современные, а скорее напоминают цепочку логических рассуждений.

Вместе с тем, если перевести в привычный нам вид те уравнения, которые умели решать в Древнем Вавилоне, то мы увидим: . И в древнем индийском манускрипте «Ариабхаттиам», датируемом 499 годом нашей эры, также встречаются задачи, решаемые с помощью квадратных уравнений. Индийские мудрецы (слово ученый тоже еще не существовало) уже не ограничивались решением конкретных житейских задач, но и работали над решением квадратного уравнения в общем виде.

Привычный нам вид уравнения обретают только в конце шестнадцатого века, благодаря трудам Франсу Виета (1540 – 1603 гг.). Именно он, помимо прочих своих научных достижений обладает и неофициальным титулом «создатель алгебры». Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».

1.Найдите уравнения, которые являются линейными.

4х + 5у = 10; ; у = 7х +4

Ответ: 4х + 5у = 10; у = 7х +4

Сегодня на уроке мы вспомним что такое линейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое линейным уравнением и неравенством.

Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.

Решением уравнения ах + by +с =0, где а,b,с – некоторые числа, называется пара значений обращающая уравнение в верное числовое равенство.

Если одновременно а и b, то уравнение ах + by +с =0 является уравнением некоторой прямой. Для построения прямой достаточно найти две точки этой прямой.

Построить график уравнения 2х+у =1

На координатной плоскости отметим точки с координатами (0;1) и (2;-3). Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1.

Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с 0, где х и у – переменные, а, b, c – некоторые числа.

Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.

Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.

Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.

Рисунок 1 – решение неравенства 3х – 2у +6 > 0

Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение ах + by +с =0, графиком которого является прямая при условии, что и . Прямая разбивает плоскость на две полуплоскости. Одна из них является графиком неравенства ах + bу + с 0

Чтобы решить неравенство ах + bу + c 0, достаточно взять какую-нибудь точку М₁(х₁; у₁), не лежащую на прямой aх + bу + c = 0, и определить знак числа aх₁ + bу₁ + c.

Источник

Линейные уравнения с двумя переменными и их системы

Вы будете перенаправлены на Автор24

Линейные уравнения с двумя переменными

Пара чисел называется решением линейного уравнения с двумя переменными, если при их подстановке в уравнение получается верное равенство.

Свойства линейных уравнений с двумя переменными:

К уравнению можно прибавлять с обоих сторон и вычитать из обоих сторон одно и тоже число.

Уравнение можно умножать и делить с обоих сторон на одно и тоже, отличное от нуля, число.

График линейного уравнения с двумя переменными

Графиком линейного уравнения с двумя переменными является множество всех точек, которые является решением данного линейного уравнения.

Видим, что мы получили уравнение линейной функции.

Готовые работы на аналогичную тему

Системы линейных уравнений с двумя переменными

Системой линейных уравнений с двумя переменными называется такая система уравнений, которая в своем составе имеет два и более линейных уравнений с двумя переменными.

Решением системы линейных уравнений называется такая пара чисел, которая является решением всех уравнений, входящих в данную систему.

В дальнейшем будем рассматривать системы из двух линейных уравнений с двумя переменными.

Рисунок 3. Система имеет 1 решение

Рисунок 4. Система решений не имеет

Пример решения задачи с использованием понятия линейных уравнений с двумя переменными

Решение:

Видим, что мы получили уравнение линейной функции.

Это и есть графический вид решения системы с двумя переменными.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 03 2021

Источник

Решение простых линейных уравнений

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.