Что называется линейным неравенством с одной переменной
Линейные неравенства с одной переменной
теория по математике 📈 неравенства
Выражение с одной переменной, содержащее знак неравенства, называется неравенством с одной переменной. Например:
23х+11 9
Неравенства такого вида называют линейными неравенствами с одной переменной, так как х в них в первой степени.
Вспомним, что в зависимости от знака неравенства, их называют строгие знаки ( ) или нестрогие знаки (≤ и ≥).
Решением неравенства с одной переменной является значение переменной, при котором данное неравенство обращается в верное числовое неравенство.
Решить неравенство – это значит найти все его решения или доказать, что решений нет.
При решении неравенства с одной переменной пользуются следующими свойствами.
Рассмотрим решение линейных неравенств с одной переменной на примерах.
Пример №1. Решить неравенство:
В рассмотренных примерах мы получали неравенства, у которых коэффициент при переменной не равен нулю. Но есть случаи, когда получается неравенство вида 0•х>a или 0•х
Пример №3. Решить неравенство:
3х–15 Решить неравенство:
Выполним все необходимые действия, получим:
Данное неравенство при любом значении х будет иметь вид 0>–10, а это верное неравенство, значит х – любое число. Следовательно, ответ в данном неравенстве – «х – любое число».
Решение линейных неравенств
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Линейные неравенства — это неравенства вида:
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.
Типы неравенств
Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
Если же а b и c > d, то а + c > b + d.
Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а d, то а – c b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа
Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Правила линейных неравенств
Решение линейных неравенств
Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.
Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.
Определение 3. Линейные неравенства с одной переменной x выглядят так:
где a и b — действительные числа. А на месте x может быть обычное число.
Равносильные преобразования
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов это:
Если a ≠ 0, тогда решением будет единственный корень — х₀;
Для этого найдем значения функции в точках на промежутке;
Как решаем:
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x
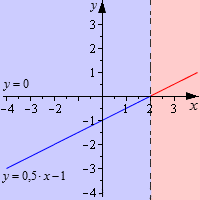
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
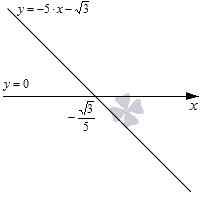
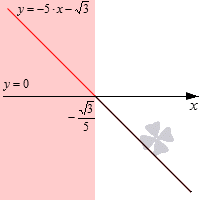
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
Ответ: (−∞, −√3 : 5) или x
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Их различия заключаются в:
Считается, что неравенства a · x + b > 0 и a · x > c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0 · x + 5 > 0 приведет к тому, что его необходимо будет решить, причем случай а = 0 не подойдет.
Как решить линейное неравенство
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Рассмотрим применение данного алгоритма на решении примеров.
Весь выше прописанный алгоритм записывается так:
Весь алгоритм запишем в краткой форме:
Ответ: неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов – это:
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Графическим способом
Алгоритм решения линейных неравенств графическим способом.
Построение графика функции y = a · x + b производится:
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Линейные неравенства (ЕГЭ 2022)
Раз уж ты читаешь эту тему, то ты наверняка уже знаком с темой «Линейные уравнения».
Если нет, то лучше скорей отправляйся исправлять это недоразумение.
Без усвоенной этой темы спокойное плавание в линейных неравенствах не гарантировано.
А если тебе все с ними понятно, вперед, покорять неравенства.
Линейные неравенства — коротко о главном
Линейными неравенствами называются неравенства вида:
где \( \displaystyle a\) и \( \displaystyle b\) – любые числа, причем \( \displaystyle a\ne 0\); \( \displaystyle x\) — неизвестная переменная.
Правила преобразования неравенств:
Правило 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные).
Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.
Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак \( \displaystyle >\) на знак \( \displaystyle 12\)
Дальше мы делим обе части составленного неравенства на \( \displaystyle 3\) и получаем:
Таким образом, каждый друг щедрого Васи получит больше, чем \( \displaystyle 4\) яблока.
Ну вот и справились с неравенством! Сейчас я введу формализованное определение линейного неравенства и будем разбираться с ним дальше.
Определение линейного неравенства:
Линейные неравенства — это неравенства вида:
Линейные неравенства, примеры, решения.
После того как получены начальные сведения о неравенствах с переменными, можно смело переходить к вопросу решения неравенств. Первыми на этом пути встают линейные неравенства с одной переменной. В этой статье мы подробно разберем, какой вид они имеют, какие методы существуют для решения линейных неравенств, дадим соответствующие алгоритмы и в деталях рассмотрим характерные примеры с решениями и пояснениями.
Сразу отметим, что здесь мы будем говорить лишь про линейные неравенства с одной переменной, а линейным неравенствам с двумя переменными выделим отдельную статью.
Навигация по странице.
Что такое линейное неравенство?
Для начала естественно определиться с тем, что же такое линейное неравенство с одной переменной. Другими словами, нужно узнать, как линейные неравенства выглядят в общем виде, чтобы можно было их отличать от других видов неравенств.
При просмотре школьных учебников по алгебре выяснилось, что определения разнятся, хотя и не принципиально. Приведем варианты определений линейного неравенства.
В учебнике Мордковича А. Г. для 9 классов приводится такое определение:
В свою очередь в учебнике алгебры для 8 классов автора Макарычева Ю. Н. линейные неравенства определяются немного иначе:
Итак, главное различие между двумя этими определениями состоит в двух моментах:
Как решить линейное неравенство?
Теперь можно разбираться, как решаются линейные неравенства a·x+b (они могут быть записаны и с помощью любого другого знака неравенства).
Основной способ их решения заключается в использовании равносильных преобразований, позволяющих прийти при a≠0 к элементарным неравенствам вида x
(≤, >, ≥), из которых делается вывод о решении исходного неравенства. Его мы и разберем в первую очередь.
Также не помешает взглянуть на решение линейных неравенств с одной переменной и с других позиций. Поэтому, мы еще покажем, как можно решить линейное неравенство графически и методом интервалов.
Используя равносильные преобразования
Пусть нам нужно решить линейное неравенство a·x+b (≤, >, ≥). Покажем, как это сделать, используя равносильные преобразования неравенства.
Полученное элементарное неравенство x≤−4 равносильно исходному линейному неравенству и является его искомым решением.
Решите неравенство 
В последнем переходе в правой части используется правило деления чисел с разными знаками 



Сформулируем приведенные рассуждения в виде алгоритма решения линейных неравенств 0·x+b (≤, >, ≥):
А теперь разберемся с этим на примерах.
В заключение этого пункта разберем решения двух линейных неравенств, оба коэффициента которых равны нулю.
Какое из линейных неравенств 0·x+0>0 и 0·x+0≥0 не имеет решений, а какое – имеет бесконечно много решений?
неравенство 0·x+0>0 не имеет решений, а неравенство 0·x+0≥0 имеет бесконечно много решений.
Методом интервалов
Вообще, метод интервалов изучается в школьном курсе алгебры позже, чем проходится тема решение линейных неравенств с одной переменной. Но метод интервалов позволяет решать самые разные неравенства, в том числе и линейные. Поэтому, остановимся на нем.
Метод интервалов подразумевает
Соберем эти моменты в алгоритм, раскрывающий как решать линейные неравенства a·x+b (≤, >, ≥) при a≠0 методом интервалов:
Так как мы решаем неравенство со знаком >, то изображаем штриховку над промежутком со знаком +, чертеж принимает вид
Графическим способом
Несложно заметить, что
Учитывая приведенную информацию, несложно сформулировать алгоритм решения линейных неравенств графическим способом:
Решите неравенство 


второе неравенство, его решением является любое действительное число.
Неравенства, сводящиеся к линейным
Огромное количество неравенств с помощью равносильных преобразований можно заменить равносильным линейным неравенством, другими словами, свести к линейному неравенству. Такие неравенства называют неравенствами, сводящимися к линейным.
Неравенства, которые подобны по виду указанным выше, всегда можно свести к линейным. Это можно сделать путем раскрытия скобок, приведения подобных слагаемых, перестановки слагаемых местами и переноса слагаемых из одной части неравенства в другую с противоположным знаком.
Из-за того, что подобные неравенства всегда можно свести к линейным, некоторые авторы даже называют их тоже линейными. Но все же будем их считать сводящимися к линейным.
Теперь становится понятно, почему подобные неравенства рассматривают вместе с линейными неравенствами. Да и принцип их решения абсолютно такой же: выполняя равносильные преобразования, их можно привести к элементарным неравенствам, представляющим собой искомые решения.
Чтобы решить неравенство подобного вида можно его предварительно свести к линейному, после чего решить это линейное неравенство. Но рациональнее и удобнее поступать так: