Что называется коэффициентами искажения

ПОКАЗАТЕЛИ ИСКАЖЕНИЯ ПО АКСОНОМЕТРИЧЕСКИМ ОСЯМ

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

Аксонометрические изображения довольно широко применяются в конструкторской работе. Это объясняется тем, что они обладают большой наглядностью и сравнительно простым построением.

Особое значение приобретают аксонометрические изображения еще и потому, что в наши дни все большее внимание уделяется вопросам эстетики промышленных форм, внешнего вида изделий (дизайну).

Рассмотрим пример получения аксонометрической проекции.

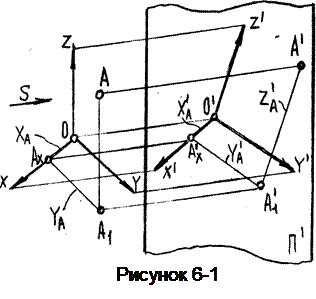
Возьмем точку А, отнесенную к пространственной системе прямоугольных координат XYZ. Выберем плоскость проекций П’ и спроецируем на нее по некоторому данному направлению S, точку А с системой прямоугольных координат (рисунок 6-1).

Из построения следует, что каждой точке А пространства на плоскости проекций П’ соответствует определенная точка А’. Однако обратное утверждение будет неверно т.к. точке А’ на П’ соответствует любаяточка проецирующего луча АА’.

ПОКАЗАТЕЛИ ИСКАЖЕНИЯ ПО АКСОНОМЕТРИЧЕСКИМ ОСЯМ

В общем случае длина отрезков осей координат в пространстве не равна длине их проекций. Искажение отрезков осей координат при их проецировании на П’ характеризуется коэффициентами искажения.

Коэффициентом искажения называется отношение длины проекции отрезка оси к его натуральной длине.

Приняты коэффициенты искажения по осям:

· По осиX:U =О’Х’/ОХ=О’А’х/ОАх=Х’АХА;

· По оси Y: V=O’Y’/OY=A’xA’/AxA=Y’A/YA

· По оси Х: W=O’Z’/OZ=A’1A/A1A=Z’AZA.

В зависимости от соотношения коэффициентов искажения по осям различают три вида аксонометрических проекций:

3) триметрические – коэффициенты искажения по всем осям различны-

Дата добавления: 2015-11-06 ; просмотров: 1438 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

коэффициент искажения

3.4 коэффициент искажения: Отношение длины проекции отрезка оси на плоскость к его истинной длине.

3.6.4 коэффициент искажения: Отношение среднеквадратического значения высших гармоник (получаемого выделением из несинусоидальной переменной величины основной гармоники) к среднеквадратическому значению несинусоидальной величины. Коэффициент искажения обычно выражают в процентах.

Смотри также родственные термины:

Коэффициент искажения синусоидальной кривой напряжения

Коэффициент искажения синусоидальной кривой тока

Коэффициент искажения синусоидальности кривой напряжения

55. Коэффициент искажения синусоидальности кривой напряжения (тока)

E. Distortion factor (of a non-sinusoidal alternating voltage or current)

F. Facteur de distortion (d’une tension ou d’un courant alternative non sinusoïdal)

Величина, равная отношению действующего значения суммы гармонических составляющих к действующему значению основной составляющей переменного напряжения (тока).

Примечание. Для целей стандартизации допускается относить к номинальному напряжению (току)

126 коэффициент искажения синусоидальности кривой напряжения (тока) К _UИ, К_IИ

Коэффициент искажения: Величина, равная отношению действующего значения суммы гармонических составляющих к действующему значению основной составляющей переменного напряжения (тока).

en. Distortion factor (of a non-sinusoidal alternating voltage or current)

fr. Facteur de distortion (d’une tension ou d’un courant alternatif non sinusoidal)

Коэффициент искажения синусоидальности кривой тока

Полезное

Смотреть что такое «коэффициент искажения» в других словарях:

коэффициент искажения — отношение среднего квадратического значения содержащихся гармоник (получаемого путем вычитания из несинусоидальной переменной величины ее основной составляющей) к среднему квадратическому значению несинусоидальной величины. Коэффициент искажения… … Справочник технического переводчика

коэффициент искажения синусоидальности кривой напряжения (тока) — Величина, равная отношению действующего значения суммы гармонических составляющих к действующему значению основной составляющей переменного напряжения (тока). Примечание. Для целей стандартизации допускается относить к номинальному напряжению… … Справочник технического переводчика

коэффициент искажения синусоидальности кривой напряжения (тока) — Величина, равная отношению действующего значения суммы гармонических составляющих к действующему значению основной составляющей переменного напряжения (тока). Примечание. Для целей стандартизации допускается относить к номинальному напряжению… … Справочник технического переводчика

Коэффициент искажения синусоидальности кривой напряжения — 126 Источник: ГОСТ Р 54130 2010: Качество электрической энергии. Термины и определения оригинал документа Смотри также родственные термины … Словарь-справочник терминов нормативно-технической документации

коэффициент искажения амплитуды — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN amplitude distortion factor … Справочник технического переводчика

коэффициент искажения входного тока полупроводникового преобразователя — Отношение действующего значения основной гармоники входного тока полупроводникового преобразователя к действующему значению. [ГОСТ 23414 84] Тематики преобразователь электроэнергии … Справочник технического переводчика

коэффициент искажения синусоидальности кривой напряжения — [Интент] Тематики качество электрической энергии EN THD voltageTHDUTHDVtotal harmonic voltage distortion … Справочник технического переводчика

коэффициент искажения синусоидальности кривой тока — [Интент] Тематики качество электрической энергии EN THD currentTHDItotal harmonic current distortion … Справочник технического переводчика

Коэффициент искажения синусоидальной кривой напряжения — 55 Источник: ГОСТ 23875 88: Качество электрической энергии. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Коэффициент искажения синусоидальной кривой тока — 55 Источник: ГОСТ 23875 88: Качество электрической энергии. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Источник

Аксонометрические проекции

Комплексный чертеж является графически простым и удобно из­меряемым. Но по нему не всегда легко представить предмет в простран­стве. Необходим чертеж, дающий и наглядное представление.

Он может быть получен при проецировании предмета вместе с осями координат на одну плоскость. В этом случае на одной проекции можно получить на­глядное и метрически определенное изображение. Такие виды изображе­ний называют аксонометрическими проекциями.

Слово «аксонометрия» (от гр. axon — ось и metreo — измеряю) пере­водится как «измерение по осям».

Способ аксонометрического проецирования состоит в том, что фи­гура вместе с осями прямоугольных координат (к которым она отнесена в пространстве) проецируется на некоторую плоскость. Эту плоскость называют плоскостью аксонометрических проекций, или картинной плоскостью.

При проецировании фигуры проецирующие лучи могут выходить из одной точки — центральная аксонометрия или быть параллельными друг другу — параллельная аксоносметрия. В дальнейшем мы будем рас­сматривать только параллельную аксонометрию.

Построим аксонометрическую проекцию точки A, отнесенной к трем взаимно перпендикулярным плоскостям проекций (рис. 1).

Введем некоторые наименования:

Q — плоскость аксонометрических проекций (картинная плос­кость);

I — направление проецирования

α — угол наклона направления проецирования I к плоскости аксо­нометрических проекций Q (картинной плоскости).

Из точек о, а_х, а_у, а_z — проведем проецирующие лучи до пересечения с плоскостью Q и найдем аксонометрические проекции этих точек о₁, а_х1, а_y1, а_z1.

х_1, у₁, z₁ — аксонометрические оси координат (аксонометрические оси);

А₁ — аксонометрическая проекция точки А;

В зависимости от положения плоскостей проекций Н, V, W, плос­кости аксонометрических проекций Q и направления проецирования I координаты точки будут проецироваться с различными искажениями. Чтобы учесть эти факторы на осях координат отложим масштабные от­резки и построим их аксонометрические проекции.

При построении аксонометрии фигуры учитывают не длины мас­штабных отрезков, а отношение длины аксонометрической проекции масштабного отрезка к его действительной величине. Эти отношения на­зываются коэффициентом искажения по оси.

Обозначим эти коэффициенты:

В зависимости от направления проецирования по отношению к плоскости аксонометрических проекций Q аксонометрические проекции делятся на:

Доказано, что сумма квадратов коэффициентов искажения удовле­творяет уравнениям:

Основная теорема аксонометрии

Занимаясь теорией аксонометрии, немецкий геометр К. Польке в 1853 году предложил и доказал для частного случая теорему, названную основной теоремой аксонометрии: «Любые три отрезка, выходящие из одной точки на плоскости, могут быть приняты за параллельные проек­ции трех равных и взаимно перпендикулярных отрезков в пространстве».

Доказательство этой теоремы в общем виде было дано в 1864 г. другим немецким геометром Г. Шварцем. С этого времени основная теорема ак­сонометрии стала называться теоремой Польке — Шварца.

Из рассмотренного выше можно вывести определение аксономет­рии:

Аксонометрией называется изображение предмета на плоскости, отнесенное к определенной системе координат и выполненное в опреде­ленном масштабе с учетом коэффициентов искажения.

В зависимости от соотношения между коэффициентами искажения по осям различают следующие аксонометрические проекции:

Наименование проекций произошло от древнегреческих слов:

«isos» — одинаковый (изометрическая проекция — проекция с оди­наковыми коэффициентами искажения по всем трем осям);

«di» — двойной (диметрическая проекция — проекция с одинаковы­ми коэффициентами искажения по двум осям);

«treis» — три (триметрическая проекция — проекция с разными ко­эффициентами искажения по всем трем осям).

Источник

Черчение. 10 класс

§ 17. Основные положения аксонометрического проецирования

Основные положения аксонометрического проецирования

Проецирование предмета на плоскости проекций дает нам представление о форме самого предмета только с одной стороны. Чтобы получить представление о форме предмета в целом, нужно проанализировать и сравнить между собой отдельные его проекции. Предмет можно спроецировать на плоскость проекций таким образом, чтобы на созданном изображении было видно сразу несколько его сторон. Полученное таким образом изображение называется наглядным. Его используют для реализации технического замысла автора при выполнении проектирования и конструирования разных объектов (рис. 53).
Для получения наглядного изображения предмета используют аксонометрическую проекцию (рис. 54).

Аксонометрическая проекция — это изображение, полученное при параллельном проецировании предмета вместе с осями прямоугольных координат на произвольную плоскость.

Слово аксонометрия — греческое. В переводе оно означает «измерение по осям» (аксон — ось, метрео — измеряю).

Проецируемый предмет располагают относительно координатных осей х, у, z и вместе с ними проецируют его на произвольную плоскость. Эта плоскость называется плоскостью аксонометрических проекций. Проекции координатных осей называются аксонометрическими осями (см. рис. 54).

Виды аксонометрических проекций.

Аксонометрическое изображение предмета получается прямоугольным (а) и косоугольным (б) проецированием.
Проецирующие лучи в прямоугольной аксонометрической проекции перпендикулярны плоскости проекции. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая проекции.
Проецирующие лучи в косоугольной аксонометрической проекции направлены под углом к плоскости проекций. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

Какой вид аксонометрической проекции (прямоугольную или косоугольную) вы будете использовать для наглядного изображения объекта? Свой выбор объясните.

Коэффициент искажения. Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям.

Коэффициент искажения (k) — отношение аксонометрической единицы измерения к натуральной.

В зависимости от расположения координатных аксонометрических осей относительно аксонометрических проекций получаются различные аксонометрические проекции: прямоугольная изометрическая проекция (сокращенно — изометрия), прямоугольная диметрическая проекция (или диметрия), косоугольные фронтальная и горизонтальная изометрия и фронтальная диметрия.
Например, в прямоугольной изометрической проекции оксонометрические оси располагаются по отношению друг к другу под углом 120°.
Коэффициенты искажения различны в изометрических и диметрических аксонометрических проекциях. В изометрической проекции коэффициент (k) равен единице, т. е. по осям х, y, z выполняют проекцию без искажения. Диметрическая проекция выполняется с коэффициентом искажения (k) по оси y, равным 0,5, а по осям z и х — равным единице.

Объясните, в чем отличие изометрической проекции от диметрической.

Наиболее распространенными являются прямоугольная изометрическая (прямоугольная изометрия) и косоугольная фронтальная диметрическая (фронтальная диметрия) проекции, в которых объект изображается в трех проекциях так, чтобы можно было хорошо увидеть его форму с трех сторон.
Способы построения аксонометрических осей. При построении аксонометрических осей прямоугольной изометрии используют один из трех способов.

Правила построения аксонометрических проекций
1. Длина откладывается по оси х, высота — по оси z, ширина — по оси у.
2. Все измерения выполняются только по аксонометрическим осям или прямым, параллельным им.
3. Все прямые линии, параллельные друг другу или осям x, y, z, на комплексном чертеже в аксонометрических проекциях остаются параллельными между собой и соответствующим аксонометрическим осям

В начале 80-х гг. XX в. в компьютерных играх стала активно применяться изометрическая проекция. Это быстрая и эффективная симуляция трехмерного пространства, которая дает иллюзию глубины без большого количества дорогостоящих вычислений. Раньше большинство игр имели вид сверху или вид сбоку. Первыми играми, которые использовали изометрию, были Zaxxon и Qbert. Сейчас, несмотря на развитие 3D-технологий, игры с изометрическим видом все еще очень популярны, особенно ролевые и стратегии.

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник