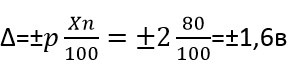Классы точности (средств измерений)

Из-за разнообразия измеряемых величин и средств измерений нельзя ввести единый способ выражения пределов допускаемых погрешностей и единые обозначения К. т. Если пределы погрешностей выражены в виде приведенной погрешности (т. е. в процентах от верхнего предела измерений, диапазона измерений или длины шкалы прибора), а также в виде относительной погрешности (т. е. в процентах от действительного значения величины), то К. т. обозначают числом, соответствующим значению погрешности. Например: К. т. 0,1 соответствует погрешность 0,1%. Многие показывающие приборы (амперметры, вольтметры, манометры и др.) формируются по приведённой погрешности, выраженной в процентах от верхнего предела измерений. В этих случаях применяется ряд К. т.: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. При нормировании по относительной погрешности обозначение К. т. заключают в кружок.

Для гирь, мер длины и приборов, для которых предел погрешности выражают в единицах измеряемой величины, К. т. принято обозначать номером (1-й, 2-й и т.д. ‒ в порядке снижения К. т.). При указании конкретного К. т. слово «точность» обычно опускается, например гири 3-го класса. Ряды К. т., их обозначения и соответствующие требования к средствам измерений включаются в стандарты (ГОСТ) на отдельные их виды.

Лит.: ГОСТ 13600‒68. Государственная система обеспечения единства измерений. Средства измерений. Классы точности. Общие требования: Широков К. П. и Раинович С. Г., О классах точности средств измерений, «Измерительная техника», 1969, № 4.

Полезное

Смотреть что такое «Классы точности (средств измерений)» в других словарях:

КЛАССЫ ТОЧНОСТИ (средств измерений) — КЛАССЫ ТОЧНОСТИ средств измерений, обобщенная характеристика средств измерений (см. СРЕДСТВА ИЗМЕРЕНИЙ), служащая показателем установленных для них государственными стандартами пределов основных и дополнительных погрешностей и других параметров,… … Энциклопедический словарь

Классы точности (средств измерений) — Класс точности средства измерений обобщенная характеристика прибора, характеризующая допустимые по стандарту значения основных и дополнительных погрешностей, влияющих на точность измерения. Погрешность может нормироваться, в частности, по… … Википедия

КЛАССЫ ТОЧНОСТИ — средств измерений, обобщённая хар ка средств измерений (мер, измерительных приборов), служащая показателем установленных для них гос. стандартами пределов осн. и дополнит. погрешностей и др. параметров, влияющих на точность. Напр., для концевых… … Физическая энциклопедия

КЛАССЫ ТОЧНОСТИ — средств измерений обобщенная характеристика средств измерений, служащая показателем установленных для них государственными стандартами пределов основных и дополнительных погрешностей и других параметров, влияющих на точность … Большой Энциклопедический словарь

Классы точности — I Классы точности средств измерений, обобщённая характеристика средств измерений, служащая показателем установленных для них государственными стандартами пределов основных и дополнительных погрешностей и др. параметров, влияющих на… … Большая советская энциклопедия

классы точности — I средств измерений, обобщённая характеристика средств измерений, служащая показателем установленных для них государственными стандартами пределов основной и дополнительной погрешностей и других параметров, влияющих на точность. II (в… … Энциклопедический словарь

КЛАССЫ ТОЧНОСТИ — средств измерений, обобщённая характеристика средств измерений, служащая показателем установленных для них гос. стандартами пределов осн. и доп. погрешностей и др. параметров, влияющих на точность … Естествознание. Энциклопедический словарь

Погрешности средств измерений — отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений, получаемых при помощи этих средств. Составляющие этих погрешностей, зависящие от П. с. и., называются… … Большая советская энциклопедия

ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ — отклонения метрологич. св в или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений, получаемых при помощи этих средств. Составляющие этих погрешностей, зависящие от П. с. и., наз. и н с т р у м е н т а л ь… … Физическая энциклопедия

точности классы — см. Классы точности. * * * ТОЧНОСТИ КЛАССЫ ТОЧНОСТИ КЛАССЫ, см. Классы точности (см. КЛАССЫ ТОЧНОСТИ (средств измерений)) … Энциклопедический словарь

Источник

Что нужно знать о классе точности измерительного прибора?

Измерительные приборы: вольтметры, амперметры, токовые клещи, осциллографы и другие — это устройства, предназначенные для определения искомых величин в заданном диапазоне, каждый из них имеет свою точность, причем устройства, измеряющие одну и ту же величину, в зависимости от модели, могут отличаться по точности и классу.

В каких-то ситуациях достаточно просто определить значение, например, вольтаж батарейки, а в других необходимо выполнить многократное повторение измерений высокоточными приборами для получения максимально достоверного результата, так в чем отличие таких измерительных устройств, что означает класс точности, сколько их бывает, как его определить и многое другое читайте далее в нашей статье.

Что такое класс точности

Определение: «Класс точности измерения — это общая характеристика точности средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими факторами, влияющими на нее».

Сам по себе класс не является постоянной величиной измерения, потому что само измерение зачастую зависит от множества переменных: места измерения, температуры, влажности и других факторов, класс позволяет определить лишь только в каком диапазоне относительных погрешностей работает данный прибор.

Чтобы заранее оценить погрешность, которую измерит устройство, также могут использоваться нормативные справочные значения.

Относительная погрешность — это отношение абсолютной погрешности к модулю действительного приближенного показателя полученного значения, измеряется в %.

Абсолютная погрешность рассчитывается следующим образом:

∆=±a или ∆=(a+bx)

x – число делений, нормирующее значение величины

a, b – положительные числа, не зависящие от х

Абсолютная и приведенная погрешность рассчитывается по следующим формулам, см. таблицу ниже

Какие классы точности бывают, как обозначаются

Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже

Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.

Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.

Каким ГОСТом регламентируется точность приборов?

ГОСТ 8.401-80 «Классы точности средств измерений» общие требования. Нормативным документом устанавливаются общие положения классификации точностей измерительных приборов.

Как определить класс точности электроизмерительного прибора, формулы расчета

Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.

Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12

Находим относительную погрешность:

Y= 100×0,025/12=0,208 или 2,08%

(вывод: класс точности – 2,5).

Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:

Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12

Предел абсолютной допустимой погрешности:

Относительная погрешность одного деления:

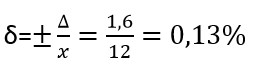
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.

Поверка приборов, для чего она нужна

Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.

Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.

Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.

Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.

Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.

Видео на тему относительная погрешность прибора

Заключение

Класс точности является важным показателем для каждого прибора, при выборе всегда обращайте внимание на него. Если вам нужен, например, электрический счетчик, важно чтобы он измерял потребление энергии с максимальной точностью, благодаря этому за весь период эксплуатации, вы сможете сэкономить приличную сумму средств.

Но, а если вам необходимо просто периодически проверять напряжение в розетке, для этого не стоит переплачивать за дорогостоящую покупку.

Источник

Класс точности

Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.

Класс точности измерительного прибора

Обобщающая характеристика, которая определяется пределами погрешностей (как основных, так и дополнительных), а также другими влияющими на точные замеры свойствами и показатели которых стандартизированы, называется класс точности измерительного аппарата. Класс точности средств измерений дает информацию о возможной ошибке, но одновременно с этим не является показателем точности данного СИ.

Средство измерения – это такое устройство, которое имеет нормированные метрологические характеристики и позволяет делать замеры определенных величин. По своему назначению они бывают примерные и рабочие. Первые используются для контроля вторых или примерных, имеющих меньший ранг квалификации. Рабочие используются в различных отраслях. К ним относятся измерительные:

На каждом средстве для измерений имеется шкала, на которой указываются классы точности этих средств измерений. Они указываются в виде чисел и обозначают процент погрешности. Для тех, кто не знает, как определить класс точности, следует знать, что они давно стандартизованы и есть определенный ряд значений. Например, на устройстве может быть одна из следующих цифр: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001. Если это число находится в круге, то это погрешность чувствительности. Обычно ее указывают для масштабных преобразователей, таких как:

Обозначение класса точности

Обязательно указывается граница диапазона работы этого прибора, в пределах которой значение класса точности будет верно.

Те измерительные устройства, которые имеют рядом со шкалой цифры: 0,05; 0,1; 0,2; 0,5, именуются как прецизионные. Сфера их применения – это точные и особо точные замеры в лабораторных условиях. Приборы с маркировкой 1,0; 1,5; 2,5 или 4,0 называются технические и исходя из названия применяются в технических устройствах, станках, установках.

Возможен вариант, что на шкале такого аппарата не будет маркировки. В такой ситуации погрешность приведенную принято считать более 4%.

Если значение класса точности устройства не подчеркнуто снизу прямой линией, то это говорит о том, что такой прибор нормируется приведенной погрешностью нуля.

Грузопоршневой манометр, класс точности 0,05

Если шкала отображает положительные и отрицательные величины и отметка нуля находится посередине такой шкалы, то не стоит думать, что погрешность во всем диапазоне будет неизменной. Она будет меняться в зависимости от величины, которую измеряет устройство.

Если замеряющий агрегат имеет шкалу, на которой деления отображены неравномерно, то класс точности для такого устройства указывают в долях от длины шкалы.

Возможны варианты измерительных аппаратов со значениями шкалы в виде дробей. Числитель такой дроби укажет величину в конце шкалы, а число в знаменателе при нуле.

Нормирование

Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й

Нормирование осуществляется по:

Формулы расчета абсолютной погрешности по ГОСТ 8.401

Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.

Виды маркирования

Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.

Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.

Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.

Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.

Пределы

Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

Базовый способ определения погрешности

При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.

Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.

Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.

Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.

Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.

Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.

Пример расчета погрешности

Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.

Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.

Классы точности болтов

Болты и другие крепежные изделия изготавливают нескольких классов:

Каждый из них имеет свои допуски измеряемой величины, отличные от остальных и применяется в различных сферах.

Крепеж С используют в отверстиях с диаметром немногим больше диаметра болта (до 3мм). Болты без труда устанавливаются, не отнимая много времени на работу. Из минусов стоит отметить то, что при физическом воздействии на такой крепеж, болтовое соединение может сместиться на несколько миллиметров.

Крепеж В подразумевает использование болтов, диаметр которых меньше отверстия в пределах 1-1,5 мм. Это позволяет конструкции меньше подвергаться смещениям и деформациям, но повышаются требования к изготовлению отверстий в креплениях.

Гайки шестигранные класса точности В

Крепеж А создается по проекту. Диаметр болта такого типа, меньше диаметра отверстия максимум на 0,3 мм и имеет допуск только со знаком минус. Это делает крепеж неподвижным, не позволяет происходить смещению узлов. Изготовление болтов А-класса стоит дороже и не всегда используется в производстве.

Класс точности присутствует в описании всех измерительных приборов и является одной из самых важных характеристик. Чем выше его значение, тем более дорогостоящий будет прибор, но в то же время он сможет предоставить более точную информацию. Выбор стоить делать исходя из сложившейся ситуации и целей в которых будет использоваться такое средство. Важно понимать, что в некоторых ситуациях экономически выгодно будет приобрести дорогостоящее сверхточное оборудование, чтобы в дальнейшем сберечь деньги.

Источник

Что означает класс точности измерительного прибора

Класс точности измерительного прибора — это обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых установлены в стандартах на отдельные виды средств измерений. Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.

Основные способы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ.

На шкале измерительного прибора маркируют значение класса точности измерительного прибора в виде числа, указывающего нормированное значение погрешности. Выраженное в процентах, оно может иметь значения 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001 и т. д.

Если обозначаемое на шкале значение класса точности обведено кружком, например 1,5, это означает, что погрешность чувствительности δ s =1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, измерительных шунтов, измерительных трансформаторов тока и напряжения и т. п.).

Это означает, что для данного измерительного прибора погрешность чувствительности δ s= d x/x — постоянная величина при любом значении х. Граница относительной погрешности δ (х) постоянна и при любом значении х просто равна значению δ s, а абсолютная погрешность результата измерений определяется как d x= δ sx

Для таких измерительных приборов всегда указывают границы рабочего диапазона, в которых такая оценка справедлива.

Если на шкале измерительного прибора цифра класса точности не подчеркнута, например 0,5, это означает, что прибор нормируется приведенной погрешностью нуля δ о=0,5 %. У таких приборов для любых значений х граница абсолютной погрешности нуля d x= d о=const, а δ о= d о/хн.

Однако будет грубейшей ошибкой полагать, что амперметр класса точности 0,5 обеспечивает во всем диапазоне измерений погрешность результатов измерений ±0,5 %. Значение погрешности δ о увеличивается обратно пропорционально х, то есть относительная погрешность δ (х) равна классу точности измерительного прибора лишь на последней отметке шкалы (при х = хк). При х = 0,1хк она в 10 раз больше класса точности. При приближении х к нулю δ (х) стремится к бесконечности, то есть такими приборами делать измерения в начальной части шкалы недопустимо.

На измерительных приборах с резко неравномерной шкалой (например на омметрах) класс точности указывают в долях от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака «угол».

Источник

Что называется классом точности средства измерений

Государственная система обеспечения единства измерений

КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ

State system for ensuring the uniformity of measurements. Accuracy classes of measuring instruments. General requirements

Дата введения 1981-07-01

Постановлением Государственного комитета СССР по стандартам от 12 ноября 1980 г. N 5320 дата введения установлена 01.07.81

ПЕРЕИЗДАНИЕ. Октябрь 2010 г.

Настоящий стандарт устанавливает общие положения деления средств измерений на классы точности, способы нормирования метрологических характеристик, комплекс требований к которым зависит от класса точности средств измерений, и обозначения классов точности.

Стандарт не устанавливает классы точности средств измерений, для которых в стандартах предусмотрены нормы отдельно для систематической и случайной составляющих погрешности, а также нормирование номинальных функций влияния, если средства измерений предназначены для применения без введения поправок с целью исключения дополнительных погрешностей с учетом номинальных функций влияния. Стандарт не устанавливает также классы точности средств измерений, при применении которых в соответствии с их назначением необходимо для оценки погрешности измерений учитывать динамические характеристики.

Пояснение терминов, используемых в настоящем стандарте, приведено в приложении 4.

Стандарт полностью соответствует международной рекомендации МОЗМ N 34*.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Классы точности следует устанавливать в стандартах или технических условиях, содержащих технические требования к средствам измерений, подразделяемым по точности. Необходимость подразделения средств измерений по точности определяют при разработке этой документации.

1.1.1. Классы точности средств измерений конкретного вида следует устанавливать в стандартах общих технических требований (технических требований) или общих технических условий (технических условий).

1.1.2. Классы точности средств измерений конкретного типа следует выбирать из ряда классов точности для средств измерений конкретного вида, регламентированного в стандартах, и устанавливать в стандартах технических требований (условий) или в технической документации, утвержденной в установленном порядке.

1.1.3. В стандартах или технических условиях, устанавливающих класс точности средств измерений конкретного типа, следует давать ссылку на стандарт, которым установлен ряд классов точности на средства измерений данного вида.

1.2. Для каждого класса точности в стандартах на средства измерений конкретного вида устанавливают конкретные требования к метрологическим характеристикам, в совокупности отражающие уровень точности средств измерений этого класса. Для малоизменяющихся метрологических характеристик допускается устанавливать требования, единые для двух и более классов точности.

Независимо от классов точности нормируют метрологические характеристики, требования к которым целесообразно устанавливать едиными для средств измерений всех классов точности, например входные или выходные сопротивления.

Совокупности нормируемых метрологических характеристик должны быть составлены из характеристик, предусмотренных ГОСТ 8.009-84. Допускается включать дополнительные характеристики.

Примеры составления совокупности нормируемых метрологических характеристик, требования к которым устанавливают в зависимости от классов точности средств измерений, приведены в приложении 1.

1.3. Средствам измерений с двумя или более диапазонами измерений одной и той же физической величины допускается присваивать два или более класса точности (см. приложение 2, п.1).

1.4. Средствам измерений, предназначенным для измерений двух или более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины (см. приложение 2, п.2).

1.5. С целью ограничения номенклатуры средств измерений по точности для средств измерений конкретного вида следует устанавливать ограниченное число классов точности, определяемое технико-экономическими обоснованиями.

1.6. Средства измерений должны удовлетворять требованиям к метрологическим характеристикам, установленным для присвоенного им класса точности, как при выпуске их из производства, так и в процессе эксплуатации.

1.7. Классы точности цифровых измерительных приборов со встроенными вычислительными устройствами для дополнительной обработки результатов измерений следует устанавливать без учета режима обработки.

1.8. Классы точности следует присваивать средствам измерений при их разработке с учетом результатов государственных приемочных испытаний. Если в стандарте или технических условиях, регламентирующих технические требования к средствам измерений конкретного типа, установлено несколько классов точности, то допускается присваивать класс точности при выпуске из производства, а также понижать класс точности по результатам поверки в порядке, предусмотренном документацией, регламентирующей поверку средств измерений. При этом класс точности набора мер определяется классом точности меры с наибольшей погрешностью (см. приложение 2, п.3).

2. СПОСОБЫ НОРМИРОВАНИЯ И ФОРМЫ ВЫРАЖЕНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК

2.1. Требования следует устанавливать к каждой нормируемой характеристике отдельно.

2.2. Пределы допускаемых основной и дополнительных погрешностей следует выражать в форме приведенных, относительных или абсолютных погрешностей в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений конкретного вида (см. приложение 3). Пределы допускаемой дополнительной погрешности допускается выражать в форме, отличной от формы выражения пределов допускаемой основной погрешности.

Примечание. Выражение пределов допускаемой погрешности в форме приведенных и относительных погрешностей является предпочтительным, так как они позволяют выражать пределы допускаемой погрешности числом, которое остается одним и тем же (числами, которые остаются одними и теми же) для средств измерений одного уровня точности, но с различными верхними пределами измерений.

2.3. Пределы допускаемой основной погрешности устанавливают в последовательности, приведенной ниже.

2.3.1. Пределы допускаемой абсолютной основной погрешности устанавливают по формуле

(1)

, (2)

— значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале;

В обоснованных случаях пределы допускаемой абсолютной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.

Примечание. При применении формулы (1) или (2) для средств измерений, используемых с отсчитыванием интервалов между произвольно выбираемыми отметками шкалы, допускается указывать, что погрешность каждого отдельного средства измерений не должна превышать установленной нормы, оставаясь только положительной или только отрицательной.

2.3.2. Пределы допускаемой приведенной основной погрешности следует устанавливать по формуле

, (3)

— пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1);

— нормирующее значение, выраженное в тех же единицах, что и ;

Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.

При одном и том же показателе степени допускается устанавливать не более пяти различных пределов допускаемой основной погрешности для средств измерений конкретного вида.

2.3.3. Нормирующее значение для средств измерений с равномерной, практически равномерной или степенной шкалой (см. приложение 4), а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, следует устанавливать равным большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений.

Для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений нормирующее значение допускается устанавливать равным сумме модулей пределов измерений.

2.3.4. Для средств измерений физической величины, для которых принята шкала с условным нулем, нормирующее значение устанавливают равным модулю разности пределов измерений (см. приложение 2, п.4).

2.3.5. Для средств измерений с установленным номинальным значением нормирующее значение устанавливают равным этому номинальному значению (см. приложение 2, п.5).

2.3.6. Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины.

2.3.7. В случаях, не предусмотренных в пп.2.3.3-2.3.6, указания по выбору нормирующего значения должны быть приведены в стандартах на средства измерений конкретного вида.

2.3.8. Пределы допускаемой относительной основной погрешности устанавливают по формуле

, (4)

если установлено по формуле (1),

, (5)

— отвлеченное положительное число, выбираемое из ряда, приведенного в п.2.3.2;

— больший (по модулю) из пределов измерений;

;

В обоснованных случаях пределы допускаемой относительной основной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.

Соотношение между числами и следует устанавливать в стандартах на средства измерений конкретного вида.

2.4. Пределы допускаемых дополнительных погрешностей устанавливают:

в виде постоянного значения для всей рабочей области влияющей величины или в виде постоянных значений по интервалам рабочей области влияющей величины;

путем указания отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;

Источник