Что называется исходом испытания
Математика — онлайн помощь
Как любая наука, теория вероятностей имеет свои исходные понятия, через которые определяются другие понятия. К основным понятиям теории вероятностей относятся: испытание, событие, вероятность события.
Изучение явлений происходит путем наблюдений и опытов, проводимых при определенных условиях. Испытанием в теории вероятностей называется осуществление какого-либо комплекса условий, при котором наблюдается данное явление. Предполагается, что данный комплекс условий может быть воспроизведен сколь угодно большое число раз. Итак, в теории вероятностей вместо слов “произведено наблюдение при осуществлении определенного комплекса условий” говорят кратко “произведено испытание”.
Событием называется всякий факт, который может наступить в результате испытания.
События можно классифицировать по степени возможности их появления и по характеру взаимосвязи.
Достоверным называется событие, которое в данном испытании всегда наступает, его обозначают 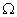
Невозможным называется событие, которое в данном испытании никогда не наступает, его обозначают 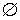
Случайным называется событие, которое в данном испытании может наступить, а может не наступить. Случайные события обозначают заглавными буквами латинского алфавита А, В, С,…
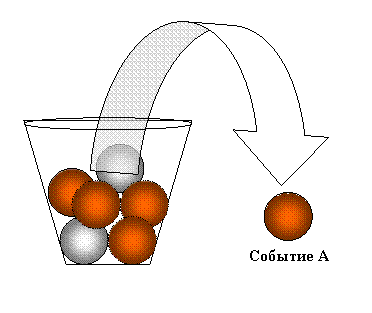
События называются несовместными, если появление одного из них исключает появление других событий в данном испытании. В противном случае события называются совместными. Примеры несовместных событий: появление герба и цифры при одном бросании монеты, попадание и промах при одном выстреле. Те же попадание и промах при двух выстрелах являются уже совместными событиями.
Несколько событий образуют полную группу событий, если в результате испытания обязательно наступит хотя бы одно из них. В частности, если события образуют полную группу и несовместны, то в результате испытания появится одно и только одно из этих событий.
Суммой событий 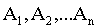
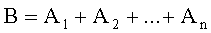
Произведением событий его обозначают 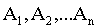
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Испытания и события
Основные понятия теории
Вероятностей
Испытания и события
Испытание (опыт, эксперимент) – реализация определенного комплекса условий, который может быть повторен неограниченное число раз. При этом комплекс условий включает в себя случайные факторы, реализация которых в каждом испытании приводит к неоднозначности исхода испытания.
Пример:
1. Подбрасывание монеты.
2. Стрельба по некоторой цели.
Событие – всякий факт, который в результате опыта может произойти или не произойти, или другими словами – это результат опыта независимо от его значения.
Пример:
1. При подбрасывании монеты событием может быть выпадение «герба», выпадение «цифры».
2. При стрельбе по некоторой цели событием может быть поражение цели, промах, поражение определенного сектора цели.
События относительно их появления подразделяется на три группы:
Достоверное событие – событие, которое всегда произойдет в результате испытания.
Пример:
1. При подбрасывании монеты выпадение «герба» или «цифры» есть событие достоверное.
2. При наблюдении за состоянием воды в сосуде при нормальном атмосферном давлении и температуре 20 0 С событие «вода в сосуде находиться в жидком состоянии» есть событие достоверное.
Невозможное событие – событие, которое никогда не произойдет в результате испытания.
Пример:
1. При подбрасывании монеты выпадение «герба» и «цифры» является событиями невозможным.
2. При наблюдении за состоянием воды при нормальном атмосферном давлении и температуре 20 0 С событие «вода в сосуде находится в твердом состоянии» является событием невозможным.
Случайное событие – событие, которое в результате испытания может произойти или не произойти, либо при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.
Пример:
1. При бросании игральной кости выпадение 6-ти очков есть событие случайное.
2. При стрельбе по цели поражение цели, попадание в определенный сектор цели являются случайными событиями.
События как объекты исследования разделяются на две группы:
Простое событие (элементарный исход) – один из возможных результатов опыта, исключающий появление других результатов. Другими словами простое событие – это результат одного и только одного опыта.
Пример:
2. При одновременном подбрасывании двух монет выпадение двух «гербов», выпадение двух «цифр» являются простыми событиями.
Сложное событие – событие, которое можно разложить на простые события. Другими словами сложное событие – это комбинация простых событий с помощью логических операций.
Пример:
1. При подбрасывании одной монеты выпадение «герба» или «цифры», а также выпадение «герба» и «цифры» есть сложные события.
2. При одновременном подбрасывании двух монет выпадение «герба» на любой из монет – это сложное событие.
События по отношению друг к другу подразделяются на :
7) образующие полную группу;
События называются несовместными,если появление одного из них исключает появление других событий в одном и том же испытании.
Пример:
2. Попадание и промах при одном выстреле – несовместные события.
3. Ни одного попадания, одно попадание, два попадания – несовместные события при двух выстрелах по мишени.
События называются совместными,если появление одного события не исключает появления других событий в данном испытании.
Пример:
2. При одновременном подбрасывании монеты и игральной кости события «выпадения 2-х очков» и «выпадение герба» являются совместными.
События в данном опыте называются равновозможными, если ни одно из них не является более возможным, чем другое.
Пример:
1. Выпадение «герба», выпадение «цифры» при бросании монеты один раз.
2. Появление 1, 2, 3, 4, 5, 6 очков при однократном бросании игральной кости.
3. Появление карты бубновой, червовой, трефовой, пиковой масти при вынимании карты из колоды.
Несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу попарно несовместны, то в результате испытания появится одно и только одно из этих событий.
Пример:
1. Выпадение «герба», выпадение «цифры» при бросании монеты образуют
полную группу событий.
2. Попадание, промах при выстреле – полная группа событий.
4. Появление не менее 3-х очков, появление не более 4-х очков при бросании игральной кости образуют полную группу событий.
Противоположными называются два несовместных события, образующих полную группу. Иногда говорят, событие 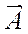
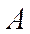
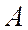
Пример:
1. Безотказная работа всех элементов технической системы, отказ хотя бы одного элемента – противоположные события.
2. Обнаружение не менее двух бракованных изделий в контрольной партии, обнаружение не более одного бракованного изделия – противоположные события.
Вероятность
Определение. Вероятность события – это численная мера степени возможности этого события.
Вероятность события 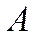

1.Вероятность достоверного события равна 1.
2.Вероятность невозможного события равна 0.
3. Вероятность случайного события есть положительное число между 0 и 1.

где 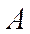
4. Вероятность любого события удовлетворяет двойному неравенству
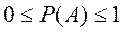
где 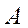
Дата добавления: 2015-11-18 ; просмотров: 3833 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Что называется исходом испытания
Событиями являются и результаты различных опытов, наблюдений и измерений.
1) из ящика с разноцветными шарами наугад вытаскивают белый шар;
2) на один из приобретенных лотерейных билетов выпал выигрыш;
3) при бросании игральной кости выпала цифра 6.
События делятся на достоверные, случайные и невозможные.
Достоверным называется событие, если оно обязательно произойдет в данном испытании.
Случайным называется событие, если оно может произойти, но может и не произойти в данном испытании.
Невозможным называется событие, если оно не может произойти в данном испытании.
За единицу принимают вероятность достоверного события, а вероятность невозможного события считают равной нулю. Тогда вероятность Р любого события А удовлетворяет неравенству:
Несовместными называются события, если появление одного из них
Пример. Опыт состоит в подбрасывании монеты, событие А – выпадение орла, событие В – выпадение решки. Эти события несовместны, равновозможны и единственно возможны.
Равновозможными называются события, если ни одно из них не является более возможным, чем другое.
Единственно возможными называются события, если в результате опыта хотя бы одно из них обязательно наступит. Говорят, что единственно возможные события образуют полную группу событий .
Рассмотрим классический метод определения вероятности некоторого случайного события. Пусть в результате некоторого опыта могут наступить события А1, А2, А3, …, Аn (элементарные исходы опыта), которые являются:
1)единственно возможными, т.е. в результате опыта хотя бы одно из них обязательно наступит;
2)несовместными, т.е. появление одного из них исключает появление всех остальных;
3)равновозможными, т.е. не существует никаких причин, в связи с которыми одно из событий появлялось бы чаще, чем остальные.
Пусть при появлении некоторых из этих событий наступает событие А. Обозначим число таких событий k (k≤n). А при появлении остальных (n-k) событий событие А не наступает. Говорят, что k событий (элементарных исходов), при которых появляется событие А, благоприятствуют событию А, а остальные (n-k) событий не благоприятствуют ему.
Вероятностью события А называется отношение числа k элементарных исходов, благоприятствующих этому событию, к общему числу элементарных исходов испытания n, если они равновозможны, несовместны и единственно возможны.
Основные понятия теории вероятностей
Что нужно знать
Это самая первая, вводная статья по теории вероятностей. Сама наука является достаточно самостоятельным разделом математики, и, чтобы понять её основы (а также для того, чтобы научиться решать простейшие задачи вроде задания 4 из ЕГЭ), нужно лишь уметь совершать арифметические действия с числами и дробями. Так что, если вам тяжело даются логарифмы и тригонометрия или совершенно непонятна производная, это никак не помешает вам разобраться в теории вероятностей.
Что вы узнаете
Что такое испытание и исход
Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание. Вообще говоря, эксперимент должен быть повторяемым. То есть, чтобы мы могли говорить о вероятности, у нас должна быть возможность провести эксперимент не один (а если совсем строго, то сколько угодно) раз.
Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: <выпало 6 6 6 > и <выпало не 6 6 6 >, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).
На столе лежит колода карт, а мы вытягиваем оттуда одну карту. Это пример случайного испытания. У этого испытания 5 2 52 5 2 исхода, так как мы можем вытянуть любую из 5 2 52 5 2 карт (в каждой из четырех мастей 1 3 13 1 3 карт от двойки до туза).
Бросок обыкновенного игрального кубика является классическим примером испытания. Сколько исходов возможно у этого испытания?
Важно понимать, что список возможных результатов мы очерчиваем сами (исходя из «здравого смысла»). Так, при броске монеты мы считаем «возможным», что она упадёт вверх аверсом («орлом») или вверх реверсом («решкой»), просто не рассматривая возможности того, что монета встанет на ребро, будет проглочена пролетающей птицей и т.п. В то же время мы считаем несущественным, упадёт монета на стол или на пол, со звоном или бесшумно и пр.; мы ограничили себя двумя интересующими нас исходами.
Рассмотрим чуть более сложный пример: мы одновременно подкинули монету и бросили игральный кубик. Сколько (и каких) исходов у этого испытания?
Для ответа на этот вопрос попробуем составить список результатов. Для монеты: Орёл (О) и Решка (Р). Для кубика: 1, 2, 3, 4, 5, 6. А теперь посмотрим, что может быть с кубиком, если монета выпала на Орла? Но ведь кубику в некотором смысле «всё равно», как выпала монета (в теории вероятностей это называется «независимые события», но об этом позже). То есть для него по-прежнему возможны все 6 вариантов. То же самое и если она выпала на Решку. Значит, можно перечислить все возможные исходы подряд, в виде «результат монеты» — «результат кубика». Сделаем это:
| О — 1 | О — 2 | О — 3 | О — 4 | О — 5 | О — 6 | всего 6 |
| Р — 1 | Р — 2 | Р — 3 | Р — 4 | Р — 5 | Р — 6 | всего 6 |
Представим следующее испытание: два игральных кубика бросают одновременно. Сколько исходов будет в этом случае?
Что такое случайное событие
Случайное событие — это подмножество множества исходов испытания.
Из скольки исходов состоит случайное событие «выпал дубль» (то есть одинаковые числа на кубиках) при испытании «бросание двух кубиков одновременно»?
Попробуйте ответить на вопрос посложнее:
Из скольки исходов состоит случайное событие «сумма очков на двух кубиках меньше 4»? Испытание то же — два кубика бросают одновременно.
Как считать вероятность события
Исходы, входящие в событие, называются благоприятными для этого события.
Прежде чем перейти к классическому определению вероятности, заметим, что для его применения требуется выполнение определённого условия — равновозможности всех исходов. Это условие может быть недостаточно строго определено, но интуитивно оно понятно. Например, если в качестве исходов при бросании монеты выбрать «орёл», «решка» и «ребро», то классическое определение вероятности применять нельзя, так как шансы на последний исход меньше, чем на первые два. А если выбрать только «орёл» и «решка», то можно — ведь нет никаких оснований считать один исход более частым, чем другой.
Итак, пусть у нас есть испытание с определённым набором равновозможных исходов. Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.
P < Событие A >= Число исходов, благоприятных для A Общее число исходов P\<\text<Событие >A\>=\frac <\text<Число исходов, благоприятных для >A><\text<Общее число исходов>> P < Событие A >= Общее число исходов Число исходов, благоприятных для A
Конечно, «в жизни» в основном встречаются ситуации, когда одни исходы встречаются чаще других, и тогда нужно использовать скорректированное определение вероятности. Но в школьных задачах исходы всегда одинаково ожидаемы, так что для нахождения вероятности нужно только правильно посчитать количество исходов, входящих в событие, и общее количество исходов испытания, после чего поделить одно на другое.
Рассмотрим пример. Из стандартной колоды карт (от двойки до туза) наугад вытащили одну карту. Какова вероятность, что эта карта — с цифрой?
Чему равна вероятность достоверного события?
Попробуйте решить несложную задачу, чтобы убедиться, что всё понятно.
В классе 21 человек, среди них 2 Саши. Классный руководитель назначил дежурной Настю и случайным образом выбирает ей напарника. Какова вероятность, что напарником окажется Саша? (Запишите ответ в виде десятичной дроби.)
Эту статью написал для вас Сергей Вальковский, учитель математики Центра образования «Пятьдесят седьмая школа», Москва.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
2. Определим еще несколько важных понятий теории вероятностей
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω=
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.
Статистическая вероятность события рассчитывается опытным путем.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов. Тогда вероятностью события А называется число
Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Примеры и разбор решения заданий тренировочного модуля
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.


