Что называется импульсом материальной точки

Импульс материальной точки – кратко формула и законы

При решении задач механического взаимодействия тел нередко возникает необходимость введения специальной величины, характеризующей количество, «объем» движения, называемой импульсом. Рассмотрим кратко это понятие.

Понятие импульса

Изучая законы механики на примере упругого столкновения движущегося и покоящегося тел (например, металлических шаров), можно легко убедиться, что результат такого столкновения зависит не только от скорости движущегося тела, но и от масс обоих тел. Чем больше масса движущегося тела, тем сильнее оно толкнет одно и то же покоящееся тело при равной скорости. Следовательно, необходимо ввести специальную величину, которая бы характеризовала эту особенность взаимодействия – количество движения или импульс.

Для вывода формулы импульса заметим, что ускорение, получаемое материальной точкой, изменяется по закону:

Это одна из записей Второго закона Ньютона. Ускорение в левой части формулы равно отношению изменения скорости ко время этого изменения. Подставляя, получим:

Преобразуя по свойству пропорции, имеем:

$$overrightarrow p= m overrightarrow v$$

Рис. 1. Импульс материальной точки.

Свойства импульса

Поскольку скорость – величина векторная, то и импульс – также векторная величина, и направлена она в том же направлении. Из этой формулы можно получить единицу измерения импульса. Масса в системе СИ измеряется в килограммах, а скорость в метрах в секунду. Значит, единица импульса – это килограмм-метр в секунду.

Если вернуться к мысленному эксперименту со столкновением покоящегося и движущегося тела, то интуитивно понятно, что если движущееся тело будет состоять из двух тел разной массы, то в результате столкновения покоящееся тело начнет двигаться вдвое быстрее, чем в случае, когда движущееся тело одно. Эксперименты подтверждают этот предположение.

Рис. 2. Упругое столкновение шаров.

Следовательно, импульс, как и сила, подчиняется принципу суперпозиции – импульс системы материальных точек равен векторной сумме отдельных импульсов каждой точки.

Импульс во Втором законе Ньютона

Заменив разность произведений масс и скоростей в формуле выше изменением импульса, получаем:

$$Δoverrightarrow p= overrightarrow F Δt$$

Изменение импульса материальной точки равно произведению силы, приложенной к этой точке на время приложения силы. Именно в таком виде второй закон Ньютона был первоначально сформулирован в труде «Математические начала натуральной философии». Измерение импульса тела проще, чем измерение ускорения, поэтому Ньютон исследовал влияние силы на тело именно по изменению импульса.

Рис. 3. Книга Ньютона Математические начала натуральной философии.

Что мы узнали?

Импульсом (или количеством движения) называется произведение массы материальной точки на ее скорость. Импульс – векторная величина, ее единицей является килограмм-метр в секунду. Импульс системы материальных точек равен векторной сумме отдельных импульсов материальных точек.

Источник

Импульс материальной точки

Всего получено оценок: 87.

Всего получено оценок: 87.

При решении задач механического взаимодействия тел нередко возникает необходимость введения специальной величины, характеризующей количество, «объем» движения, называемой импульсом. Рассмотрим кратко это понятие.

Понятие импульса

Изучая законы механики на примере упругого столкновения движущегося и покоящегося тел (например, металлических шаров), можно легко убедиться, что результат такого столкновения зависит не только от скорости движущегося тела, но и от масс обоих тел. Чем больше масса движущегося тела, тем сильнее оно толкнет одно и то же покоящееся тело при равной скорости. Следовательно, необходимо ввести специальную величину, которая бы характеризовала эту особенность взаимодействия – количество движения или импульс.

Для вывода формулы импульса заметим, что ускорение, получаемое материальной точкой, изменяется по закону:

Это одна из записей Второго закона Ньютона. Ускорение в левой части формулы равно отношению изменения скорости ко время этого изменения. Подставляя, получим:

Преобразуя по свойству пропорции, имеем:

$$\overrightarrow p= m \overrightarrow v$$

Рис. 1. Импульс материальной точки.

Свойства импульса

Поскольку скорость – величина векторная, то и импульс – также векторная величина, и направлена она в том же направлении. Из этой формулы можно получить единицу измерения импульса. Масса в системе СИ измеряется в килограммах, а скорость в метрах в секунду. Значит, единица импульса – это килограмм-метр в секунду.

Если вернуться к мысленному эксперименту со столкновением покоящегося и движущегося тела, то интуитивно понятно, что если движущееся тело будет состоять из двух тел разной массы, то в результате столкновения покоящееся тело начнет двигаться вдвое быстрее, чем в случае, когда движущееся тело одно. Эксперименты подтверждают этот предположение.

Рис. 2. Упругое столкновение шаров.

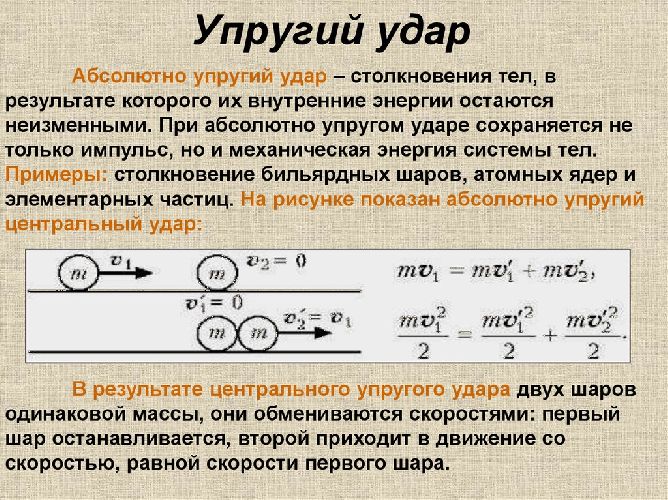
Следовательно, импульс, как и сила, подчиняется принципу суперпозиции – импульс системы материальных точек равен векторной сумме отдельных импульсов каждой точки.

Импульс во Втором законе Ньютона

Заменив разность произведений масс и скоростей в формуле выше изменением импульса, получаем:

$$Δ\overrightarrow p= \overrightarrow F Δt$$

Изменение импульса материальной точки равно произведению силы, приложенной к этой точке на время приложения силы. Именно в таком виде второй закон Ньютона был первоначально сформулирован в труде «Математические начала натуральной философии». Измерение импульса тела проще, чем измерение ускорения, поэтому Ньютон исследовал влияние силы на тело именно по изменению импульса.

Что мы узнали?

Импульсом (или количеством движения) называется произведение массы материальной точки на ее скорость. Импульс – векторная величина, ее единицей является килограмм-метр в секунду. Импульс системы материальных точек равен векторной сумме отдельных импульсов материальных точек.

Источник

Что называется импульсом материальной точки

В основе динамики материальной точки лежат законы (аксиомы) Ньютона. Напомним ключевые определения и законы.

Система отсчёта, в которой любая материальная точка, не взаимодействующая с другими телами (такая точка называется свободной), движется равномерно и прямолинейно или покоится, называется инерциальной.

инерциальные системы отсчёта (ИСО) существуют

в ИСО приращение импульса материальной точки пропорционально силе и происходит по направлению силы:

`Delta vec p = vec F * Delta t` (1)

Импульсом (или количеством движения) материальной точки называют физическую величину, определяемую произведением её массы на вектор скорости в данной системе отсчёта:

в ИСО приращение импульса материальной точки равно импульсу силы.

Отметим, что при изучении динамики второй закон Ньютона часто формулируют следующим образом:

в ИСО ускорение материальной точки прямо пропорционально сумме сил, действующих на неё, и обратно пропорционально её массе:

Если масса тела остаётся неизменной, то `Delta vec p = Delta (m vec v) = m Delta vec v`, и соотношение (1) принимает вид `m Delta vec v = vec F Delta t`. С учётом `vec a = (Delta vec v)/(Delta t)` приходим к эквивалентности соотношений (1) и (2) в рассматриваемом случае.

В настоящем Задании представлены задачи, для решения которых привлекается второй закон Ньютона (см.(1)), устанавливающий равенство приращений импульса материальной точки и импульса силы.

при взаимодействии двух материальных точек сила `vecF_(12)`, действующая на первую материальную точку со стороны второй, равна по величине и противоположна по направлению силе `vecF_(21)`, действующей со стороны первой материальной точки на вторую:

1) силы возникают парами и имеют одинаковую природу, они приложены к разным материальным точкам,

2) эти силы равны по величине,

3) они действуют вдоль одной прямой в противоположных направлениях.

Заметим, что согласно третьему закону Ньютона обе силы должны быть равны по величине в любой момент времени независимо от движения взаимодействующих тел. Другими словами, если в системе двух взаимодействующих тел изменить положение одного из тел, то это изменение мгновенно скажется на другом теле, как бы далеко оно ни находилось. На самом деле скорость распространения взаимодействий конечная; она не может превзойти скорость света в вакууме. Поэтому третий закон Ньютона имеет определённые пределы применимости. Однако в классической механике при малых скоростях взаимодействующих тел он выполняется с большой точностью.

Второй закон Ньютона (уравнение движения) можно представить в виде теоремы об изменении импульса материальной точки:

Скорость изменения импульса материальной точки в инерциальной системе отсчёта равна сумме сил, действующих на эту точку.

Напомним, что для решения задач динамики материальной точки следует:

привести «моментальную фотографию» движущегося тела, указать приложенные к нему силы;

выбрать инерциальную систему отсчёта;

составить уравнение (3);

перейти к проекциям приращения импульса и сил на те или иные направления;

решить полученную систему.

Рассмотрим характерные примеры.

На рис. 1 показаны ИСО и силы, действующие на тело в процессе разгона. По второму закону Ньютона

`(Delta vec p)/(Delta t) = M vec g + vec N + vecF_(«тр») + vec F`.

Переходя к проекциям на горизонтальную ось, находим элементарные приращения импульса в процессе разгона

и в процессе торможения `(F = 0)`

Просуммируем все приращения импульса тела от старта до остановки:

Далее рассмотрим пример, в котором одна из сил зависит от времени.

Так как `mg в импульсе силы можно интерпретировать как площадь элементарного прямоугольника со сторонами `F(t)` и `Delta t` на графике зависимости `F(t)`). Тогда импульс силы `F` за время удара равен

и в рассматриваемом случае не зависит от того, в какой именно момент времени сила достигает максимального значения (площадь треугольника равна половине произведения основания на высоту!). Далее находим импульс мяча в момент окончания действия силы

Отсюда находим начальную скорость полёта мяча

`v = (F_max * tau)/(2m) = (3,5 * 10^3 * 8 * 10^-3)/(2 * 0,5) = 28 sf»м/с»`

и максимальную дальность (старт под углом `alpha = pi/4`) полёта

В рассматриваемом модельном примере получен несколько завышенный по сравнению с наблюдениями результат.

На вступительных испытаниях и олимпиадах в вузах России регу­лярно предлагаются задачи динамики, в которых наряду с «традицион­ными» силами: силой тяжести, силой Архимеда и т. д., на тело дейст­вует сила лобового сопротивления. Такая сила возникает, например, при движении тел в жидкостях и газах. Вопрос о движении тел в жидкостях и газах имеет большое практическое значение. Знакомство с действием такого рода сил уместно начинать, как это принято в физике, с простейших модельных зависимостей, в которых сила сопротивления принимается пропорциональной скорости или её квадрату.

Мяч, брошенный с горизонтальной поверхности земли под углом `alpha = 60^@` к горизонту со скоростью `v = 10 sf»м/с»`, упал на землю, имея вертикальную составляющую скорости по абсолютной величине на `delta = 30 %` меньшую, чем при бросании. Найдите время по­лёта мяча. Считать, что сила сопротивления движению мяча пропорциональна его скорости.

Согласно второму закону Ньютона приращение импульса пропорционально силе и происходит по направлению силы:

Переходя к проекциям сил и приращения скорости на вертикальную ось, получаем

Заметим, что элементарное перемещение мяча по вертикали равно `Delta y = v_y * Delta t`, и перепишем последнее соотношение в виде:

Просуммируем все приращения вертикальной проекции импульса по всему времени полёта, т. е. от `t = 0` до `t = T`:

Переходя к конечным приращениям, получаем

Точки старта и финиша находятся в одной горизонтальной плоскости, поэтому перемещение мяча по вертикали за время полёта нулевое

Кубик, движущийся поступа­тельно со скоростью `v` (рис. 4) по гладкой горизонтальной поверхности, испытывает соударение с шероховатой вертикальной стенкой.

Коэффициент трения `mu` скольжения кубика по стенке и угол `alpha` известны. Одна из граней кубика параллельна стенке. Под каким углом `beta` кубик отскочит от стенки? Считайте, что перпендикулярная стенке составляющая скорости кубика в результате соударения не изменяется по величине.

Силы, действующие на кубик в процессе соударения, показаны на рис. 5.

По второму закону Ньютона

`Delta vec p = (m vec g + vecN_(«г») + vecF_(«тр») + vecN_(«в») ) * Delta t`.

Переходя к проекциям на горизонтальные оси `Ox` и `Oy`, получаем

Просуммируем приращения `Delta p_y = N_sf»в» Delta t` по всему времени `tau` соуда­рения, получим:

Источник

Что называется импульсом материальной точки

Роль законов сохранения в механике, да и в других разделах физики огромна.

Во-первых, они позволяют решать ряд практически важных задач, например, по первоначальному состоянию системы, не зная подробностей взаимодействия тел, определять её конечное состояние, зная скорости тел до взаимодействия, определять скорости этих тел после взаимодействия.

Во-вторых, и это главное, открытые в механике законы сохранения играют в природе огромную роль, далеко выходящую за рамки самой механики.

Они применимы как к телам обычных размеров, так и к космическим телам и элементарным частицам.

Вспомните, что такое импульс материальной точки.

С направлением какой из перечисленных величин совпадает направление импульса — силы, скорости или ускорения?

Второй закон Ньютона

m =

можно записать в иной форме, которая приведена самим Ньютоном в его главном труде «Математические начала натуральной философии».

Если на материальную точку действует постоянная сила, то постоянным будет и ускорение тела

где ₁ — начальное значение скорости материальной точки;
₂ — конечное значение скорости материальной точки.

Подставив это значение ускорения во второй закон Ньютона, получим

Импульс материальной точки — это физическая величина, равная произведению массы материальной точки на её скорость:

= m. (4.2)

Из формулы (4.2) видно, что импульс — векторная величина.
Так как m > 0, то импульс имеет такое же направление, как и скорость (рис. 4.1).

Обозначим через ₁ = m₁ импульс материальной точки в начальный момент времени, а через ₂ = m₂ — её импульс в конечный момент времени.

Δ = Δt.

Так как Δt > 0, то направления векторов Δ и совпадают.

Уравнение (4.3) показывает, что одинаковые изменения импульса могут быть получены в результате действия большой силы в течение малого интервала времени или малой силы за большой промежуток времени.

Произведение силы на время её действия называют импульсом силы.

Изменение импульса материальной точи равно импульсу действующей на нее силы.

Единица импульса не имеет особого названия, а её наименование получается из определения этой величины (см. формулу (4.2)):

1 ед. импульса = 1 кг • 1 м/с = 1 кг • м/с

Для нахождения импульса тела, которое нельзя считать материальной точкой, поступают так:
мысленно разбивают тело на отдельные малые элементы (материальные точки), находят импульсы полученных элементов, а потом суммируют их как векторы.

Поставьте на лист бумаги банку с водой.
Дёрните лист с большой силой так, чтобы он выскользнул из-под банки, а банка при этом осталась бы на месте.
Затем потяните лист так, чтобы банка двигалась вместе с листом.
Сравните время действия сил. Объясните, почему в первом случае банке не сообщается импульс, а во втором сообщается.

Импульс тела равен сумме импульсов его отдельных элементов.

Импульс системы тел равен векторной сумме импульсов каждого из тел системы:

Систему тел составляют взаимодействующие тела, движение которых мы рассматриваем.

Источник

Учебники

Журнал «Квант»

Общие

Содержание

Импульс материальной точки

Второй закон Ньютона \(

m \vec a = \vec F\) можно записать в иной форме, которая приведена самим Ньютоном в его главном труде «Математические начала натуральной философии».

Если на тело (материальную точку) действует постоянная сила, то постоянным является и ускорение

\vec \upsilon_2\) — начальное и конечное значения скорости тела.

Подставив это значение ускорения во второй закон Ньютона, получим:

В этом уравнении появляется новая физическая величина — импульс материальной точки.

Импульсом материальной точки называют величину равную произведению массы точки на ее скорость.

Обозначим импульс (его также называют иногда количеством движения) буквой \(

Из формулы (2) видно, что импульс — векторная величина. Так как m > 0, то импульс имеет то же направление, что и скорость.

Единица импульса не имеет особого названия. Ее наименование получается из определения этой величины:

Другая форма записи второго закона Ньютона

\vec p_1 = m \vec \upsilon_1\) импульс материальной точки в начальный момент интервала Δt, а через \(

\vec p_2 = m \vec \upsilon_2\) — импульс в конечный момент этого интервала. Тогда \(

Так как Δt > 0, то направления векторов \(

Согласно формуле (3)

изменение импульса материальной точки пропорционально приложенной к ней силе и имеет такое же направление, как и сила.

Именно так был впервые сформулирован второй закон Ньютона.

Произведение силы на время ее действия называют импульсом силы. Не надо путать импульс \(

Уравнение (3) показывает, что одинаковые изменения импульса материальной точки могут быть получены в результате действия большой силы в течение малого интервала времени или малой силы за большой интервал времени. Когда вы прыгаете с какой-то высоты, то остановка вашего тела происходит за счет действия силы со стороны земли или пола. Чем меньше продолжительность столкновения, тем больше тормозящая сила. Для уменьшения этой силы надо, чтобы торможение происходило постепенно. Вот почему при прыжках в высоту спортсмены приземляются на мягкие маты. Прогибаясь, они постепенно тормозят спортсмена. Формула (3) может быть обобщена и на тот случай, когда сила меняется во времени. Для этого весь промежуток времени Δt действия силы надо разделить на столь малые интервалы Δt_i, чтобы на каждом из них значение силы без большой ошибки можно было считать постоянным. Для каждого малого интервала времени справедлива формула (3). Суммируя изменения импульсов за малые интервалы времени, получим:

Символ Σ (греческая буква «сигма») означает «сумма». Индексы i = 1 (внизу) и N (наверху) означают, что суммируется N слагаемых.

Для нахождения импульса тела поступают так: мысленно разбивают тело на отдельные элементы (материальные точки), находят импульсы полученных элементов, а потом их суммируют как векторы.

Импульс тела равен сумме импульсов его отдельных элементов.

Изменение импульса системы тел. Закон сохранения импульса

При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которой мы изучаем, называется механической системой или просто системой.

Изменение импульса системы тел

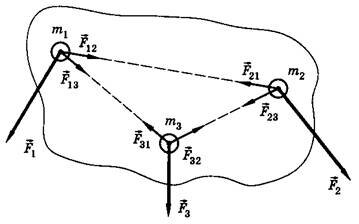
Рассмотрим систему, состоящую из трех тел. Это могут быть три звезды, испытывающие воздействие со стороны соседних космических тел. На тела системы действуют внешние силы \(

\vec F_i\) (i — номер тела; например, \(

\vec F_2\) — это сумма внешних сил, действующих на тело номер два). Между телами действуют силы \(

\vec F_\) называемые внутренними силами (рис. 1). Здесь первая буква i в индексе означает номер тела, на которое действует сила \(

Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в форме уравнения (3):

Здесь в левой части каждого уравнения стоит изменение импульса тела \(

\vec p_i = m_i \vec \upsilon_i\) за малое время Δt. Более подробно\[

\Delta (m_i \vec \upsilon_i) = m_i \vec \upsilon_ — m_i \vec \upsilon_\] где \(

\vec \upsilon_\) — скорость в начале, а \(

\vec \upsilon_\) — в конце интервала времени Δt.

Сложим левые и правые части уравнений (6) и покажем, что сумма изменений импульсов отдельных тел равна изменению суммарного импульса всех тел системы, равного

\Delta (m_1 \vec \upsilon_1) + \Delta (m_2 \vec \upsilon_2) + \Delta (m_3 \vec \upsilon_3) = m_1 \vec \upsilon_ <1k>— m_1 \vec \upsilon_ <1n>+ m_2 \vec \upsilon_ <2k>— m_2 \vec \upsilon_ <2n>+ m_3 \vec \upsilon_ <3k>— m_3 \vec \upsilon_ <3n>=\) \(

Но силы взаимодействия любой пары тел в сумме дают нуль, так как согласно формуле (5)

Поэтому изменение импульса системы тел равно импульсу внешних сил:

Мы пришли к важному выводу:

импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.

Уравнение (9) справедливо для любого интервала времени, если сумма внешних сил остается постоянной.

Закон сохранения импульса

Из уравнения (9) вытекает чрезвычайно важное следствие. Если сумма внешних сил, действующих на систему, равна нулю, то равно нулю и изменение импульса системы\[

\vec p_\) и в его конце \(

\vec p_\) один и тот же\[

Закон сохранения импульса формулируется так:

если сумма внешних сил, действующих на тела системы, равна нулю, то импульс системы сохраняется.

Тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется. Надо только помнить, что сохраняется векторная сумма импульсов, а не сумма их модулей.

Как видно из проделанного нами вывода, закон сохранения импульса является следствием второго и третьего законов Ньютона. Система тел, на которую не действуют внешние силы, называется замкнутой или изолированной. В замкнутой системе тел импульс сохраняется. Но область применения закона сохранения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю, импульс системы все равно сохраняется.

Полученный результат легко обобщается на случай системы, содержащей произвольное число N тел:

\vec \upsilon_\) — скорости тел в начальный момент времени, а \(

\vec \upsilon_\) — в конечный. Так как импульс — величина векторная, то уравнение (11) представляет собой компактную запись трех уравнений для проекций импульса системы на координатные оси.

Когда выполняется закон сохранения импульса?

Все реальные системы, конечно, не являются замкнутыми, сумма внешних сил довольно редко может оказаться равной нулю. Тем не менее в очень многих случаях закон сохранения импульса можно применять.

Если сумма внешних сил не равна нулю, но равна нулю сумма проекций сил на какое-то направление, то проекция импульса системы на это направление сохраняется. Например, система тел на Земле или вблизи ее поверхности не может быть замкнутой, так как на все тела действует сила тяжести, которая изменяет импульс по вертикали согласно уравнению (9). Однако вдоль горизонтального направления сила тяжести не может изменять импульс, и сумма проекций импульсов тел на горизонтально направленную ось будет оставаться неизменной, если действием сил сопротивления можно пренебречь.

Кроме того, при быстрых взаимодействиях (взрыв снаряда, выстрел из орудия, столкновения атомов и т. п.) изменение импульсов отдельных тел будет фактически обусловлено только внутренними силами. Импульс сис-темы сохраняется при этом с большой точностью, ибо такие внешние силы, как сила тяготения и сила трения, зависящая от скорости, заметно не изменяет импульса системы. Они малы по сравнению с внутренними силами. Так, скорость осколков снаряда при взрыве в зависимости от калибра может изменяться в пределах 600 — 1000 м/с. Интервал времени, за который сила тяжести смогла бы сообщить телам такую скорость, равен

Внутренние же силы давления газов сообщают такие скорости за 0,01 с, т.е. в 10000 раз быстрее.

Реактивное движение. Уравнение мещерского. Реактивная сила

Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела,

например при истечении продуктов сгорания из сопла реактивного летательного аппарата. При этом появляется так называемая реактивная сила, сообщающая телу ускорение.

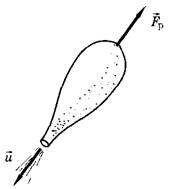
Наблюдать реактивное движение очень просто. Надуйте детский резиновый шарик и отпустите его. Шарик стремительно взовьется вверх (рис. 2). Движение, правда, будет кратковременным. Реактивная сила действует лишь до тех пор, пока продолжается истечение воздуха.

Главная особенность реактивной силы состоит в том, что она возникает без какого-либо взаимодействия с внешними телами. Происходит лишь взаимодействие между ракетой и вытекающей из нее струей вещества.

Сила же, сообщающая ускорение автомобилю или пешеходу на земле, пароходу на воде или винтовому самолету в воздухе, возникает только за счет взаимодействия этих тел с землей, водой или воздухом.

При истечении продуктов сгорания топлива они за счет давления в камере сгорания приобретают некоторую скорость относительно ракеты и, следовательно, некоторый импульс. Поэтому в соответствии с законом сохранения импульса сама ракета получает такой же по модулю импульс, но направленный в противоположную сторону.

Масса ракеты с течением времени убывает. Ракета в полете является телом переменной массы. Для расчета ее движения удобно применить закон сохранения импульса.

Уравнение Мещерского

Выведем уравнение движения ракеты и найдем выражение для реактивной силы. Будем считать, что скорость вытекающих из ракеты газов относительно ракеты постоянна и равна \(

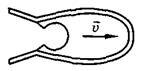
Пусть в некоторый момент времени скорость ракеты относительно инерциальной системы, связанной со звездами, равна \(

\vec \upsilon\) (рис. 3), а масса ракеты равна М. Через малый интервал времени Δt масса ракеты станет равной

где μ — расход топлива (расходом топлива называется отношение массы сгоревшего топлива ко времени его сгорания).

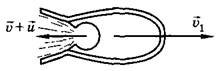
За этот же промежуток времени скорость ракеты изменится на \(

\Delta \vec \upsilon\) и станет равной \(

\vec \upsilon + \vec u\) (рис. 4), так как до начала сгорания топливо имело ту же скорость, что и ракета.

Запишем закон сохранения импульса для системы ракета — газ:

Раскрыв скобки, получим:

\mu \Delta t \vec \upsilon\) можно пренебречь по сравнению с остальными, так как оно содержит произведение двух малых величин (это величина, как говорят, второго порядка малости). После приведения подобных членов будем иметь:

Это одно из уравнений Мещерского для движения тела переменной массы, полученное им в 1897 г.

Если ввести обозначение \(

\vec u\) при расходе топлива μ. Реактивная сила космических ракет достигает 1000 кН.

Если на ракету действуют внешние силы, то ее движение определяется реактивной силой и суммой внешних сил. В этом случае уравнение (12) запишется так:

Реактивные двигатели

Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Применяются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-реактивными двигателями.

В космическом пространстве использовать какие-либо другие двигатели, кроме реактивных, невозможно: нет опоры (твердой, жидкой или газообразной), отталкиваясь от которой космический корабль мог бы получить ускорение. Применение же реактивных двигателей для самолетов и ракет, не выходящих за пределы атмосферы, связано с тем, что именно реактивные двигатели способны обеспечить максимальную скорость полета.

Реактивные двигатели делятся на два класса: ракетные и воздушно-реактивные.

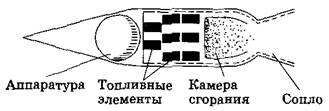
В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.

При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где расположено сопло. Вытекающие через сопло газы не встречают на своем пути стенку, на которую могли бы оказывать давление. В результате появляется сила, толкающая ракету вперед.

Суженная часть камеры — сопло служит для увеличения скорости истечения продуктов сгорания, что в свою очередь повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.

Применяются также ракетные двигатели, работающие на жидком топливе.

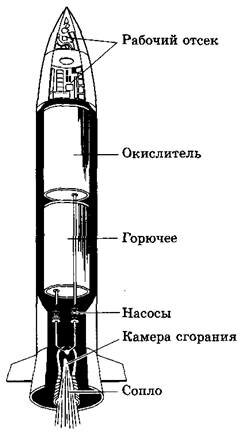
В жидкостно-реактивных двигателях (ЖРД) в качестве горючего можно использовать керосин, бензин, спирт, анилин, жидкий водород и др., а в качестве окислителя, необходимого для горения, — жидкий кислород, азотную кислоту, жидкий фтор, пероксид водорода и др. Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру, где при сгорании топлива развивается температура до 3000 °С и давление до 50 атм (рис. 6). В остальном двигатель работает так же, как и двигатель на твердом топливе.

Жидкостно-реактивные двигатели используются для запуска космических кораблей.

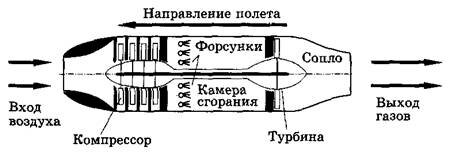
Воздушно-реактивные двигатели в настоящее время применяют главным образом на самолетах. Основное их отличие от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы. На рисунке 7 изображена схема воздушно-реактивного двигателя турбокомпрессорного типа. В носовой части расположен компрессор, засасы-вающий и сжимающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (обычно используется керосин) подается в камеру сгорания с помощью специальных форсунок.

Раскаленные газы (продукты сгорания), выходя через сопло, вращают газовую турбину, приводящую в движение компрессор. Турбокомпрессорные двигатели установлены в наших лайнерах Ту-134, Ил-62, Ил-86 и др.

Реактивными двигателями оснащены не только ракеты, но и большая часть современных самолетов.

Успехи в освоении космического пространства

Автором первого в мире проекта реактивного летательного аппарата для полета людей был русский революционер-народоволец Н.И. Кибальчич (1853—1881).

Основы теории реактивного двигателя и научное доказательство воз-можности полетов в межпланетном пространстве были впервые высказаны и разработаны русским ученым К.Э. Циолковским в работе «Исследование мировых пространств реактивными приборами».

К.Э. Циолковскому принадлежит также идея применения многоступенчатых ракет. Отдельные ступени, из которых составлена ракета, снабжаются собственными двигателями и запасом топлива. По мере выгорания топлива каждая очередная ступень отделяется от ракеты. Поэтому в дальнейшем на ускорение ее корпуса и двигателя топливо не расходуется.

Идея Циолковского о сооружении большой станции-спутника на орбите вокруг Земли, с которой будут стартовать ракеты к другим планетам Солнечной системы, еще не осуществлена, но нет сомнения в том, что рано или поздно такая станция будет создана.

В настоящее время становится реальностью пророчество Циолковского: «Человечество не останется вечно на Земле, но в погоне за светом и пространством сначала робко проникнет за пределы атмосферы, а затем завоюет себе все околосолнечное пространство».

Нашей стране принадлежит великая честь запуска 4 октября 1957 г. первого искусственного спутника Земли. Также впервые в нашей стране 12 апреля 1961 г. был осуществлен полет космического корабля с космонавтом Ю.А. Гагариным на борту.

Эти полеты были совершены на ракетах, сконструированных отечест-венными учеными и инженерами под руководством С.П. Королева. Большие заслуги в исследовании космического пространства имеют американские ученые, инженеры и астронавты. Два американских астронавта из экипажа космического корабля «Аполлон-11» — Нейл Армстронг и Эдвин Олдрин — 20 июля 1969 г. впервые совершили посадку на Луну. На космическом теле Солнечной системы человеком были сделаны первые шаги.

С выходом человека в космос не только открылись возможности исследования других планет, но и представились поистине фантастические возможности изучения природных явлений и ресурсов Земли, о которых можно было только мечтать. Возникло космическое природоведение. Раньше общая карта Земли составлялась по крупицам, как мозаичное панно. Теперь снимки с орбиты, охватывающие миллионы квадратных километров, позволяют выбирать для исследования наиболее интересные участки земной поверхности, экономя тем самым силы и средства- Из космоса лучше различаются крупные геологические структуры: плиты, глубинные разломы земной коры — места наиболее вероятного залегания полезных ископаемых. Из космоса удалось обнаружить новый тип геологических образований кольцевые структуры, подобные кратерам Луны и Марса,

Сейчас на орбитальных комплексах разработаны технологии получения материалов, которые нельзя изготовить на Земле, а только в состоянии длительной невесомости в космосе. Стоимость этих материалов (сверхчистые монокристаллы и др.) близка к затратам на запуск космических аппаратов.

Источник