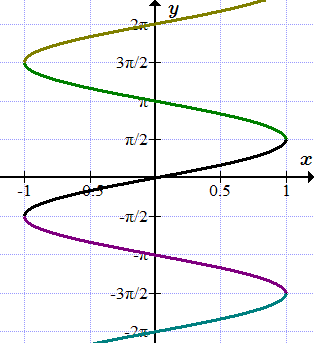Что называется функцией в математике
Что такое Функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
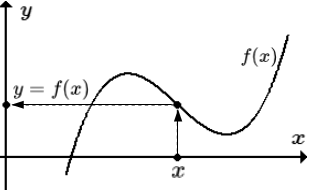
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Что такое функция
Понятие функции – одно из основных в математике.
На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.
Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.
1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.
Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.
2. Можно дать и другое определение.
Функция – это определенное действие над переменной.
Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.
3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.
Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.
Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.
А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:
Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.
Очень сложно было бы описать такое соответствие математически, не правда ли?
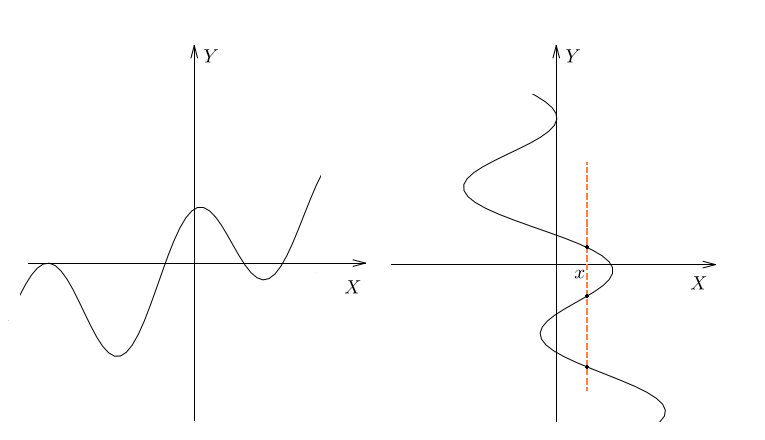
Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?
Ты нашел то, что искал? Поделись с друзьями!
Перечислим способы задания функции.
Это примеры функций, заданных формулами.
К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.
Что такое функция в математике
Понятие функции в математике появилось не просто так. Давайте разберемся, зачем придумали функцию и как с ней можно работать.
| Сколько времени двигается автомобиль | Сколько км проедет автомобиль |
|---|---|
| 1 час | 60 км |
| 2 часа | 120 км |
| 3 часа | 180 км |
Если внимательно изучить таблицу станет очевидно, что между временем автомобиля в пути и пройденным расстоянием есть четкая зависимость.
Обозначим за « x » время автомобиля в пути.
Обозначим за « y » расстояние, пройденное автомобилем.
Запишем зависимость « y » (расстояния) от « x » (времени в пути автомобиля).
Давайте убедимся, что мы правильно записали зависимость пройденного расстояния от времени в пути.
Теперь вместо « y » запишем обозначение « y(x) ». Такая запись означает, что « y » зависит от « x ».
Окончательная запись нашей функции, которая показывает зависимость пройденного автомобилем расстояния от времени в пути, выглядит следующим образом:
Функцией называют зависимость « y » от « x ».
Запись функции в виде « y(x) = 60x » называют формульным способом задания функции.
Конечно, нужно понимать, что функция « y(x) = 60x » — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.
Примеры других функций:
Единственное, что объединяет все функции, это то, что они показывают зависимость значения функция (« y ») от её аргумента (« x »).
Способы задания функции
Задание функции формулой
Через формульный способ задания функции всегда можно сразу по конкретному значению аргумента « x » найти значение функции « y ».
Например, рассмотрим функцию, заданную формульным способом.
Запишем расчет следующим образом.
Табличный способ задания функции
С табличным способом задания функции мы уже встречались, когда расписывали таблицу для функции, которая описывает движение автомобиля « y(x) = 60x ».
Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений « y » для произвольно выбранных значений « x ».
Будьте внимательны, когда подставляете значение « x » в функцию,
у которой перед « x » есть минус.
Нельзя терять знак минуса, который стоит перед « x ».
При подстановки отрицательного числа в функцию вместо « x » обязательно заключайте отрицательное число в скобки. Не забывайте использовать правило знаков.
Подставим в функцию « y(x) = −x + 4 » вместо « x » отрицательное число « −1 ».
Неправильно
Правильно
Запишем полученные результаты в таблицу. Таким образом мы получили табличный способ задания функции « y(x) = −x + 4 ».
| x | y |
|---|---|
| −1 | 5 |
| 0 | 4 |
| 1 | 3 |
Графический способ задания функции
Теперь давайте разберемся, что называют графиком функции и как его построить.
Прежде чем перейти к изучению графического способа задания функции обязательно вспомните, что называют прямоугольной системой координат.
Рассмотрим функцию « y(x) = −2x + 1 ».
Результаты запишем в таблицу.
| x | Расчет |
|---|---|
| −1 | y(−1) = −2 · (−1) + 1 = 2 + 1 = 3 |
| 0 | y(0) = −2 · 0 + 1 = 0 + 1 = 1 |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Назовем каждую полученную точку и запишем их координаты в новую таблицу.
| Имя точки | x | y |
|---|---|---|
| (·) A | −1 | 3 |
| (·) B | 0 | 1 |
| (·) C | 1 | −1 |
Соединим отмеченные точки прямой. Проведенная прямая будет графиком функции « y(x) = −2x + 1 ».
График функции — это объединение всех точек, координаты которых мы можем найти, подставляя в функцию произвольные числовые значения вместо « x ».
Другими словами можно сказать, что под графиком функции мы понимаем множество всех точек, координаты которых мы можем найти, подставляя в функцию любые числовые значения вместо « x ».
Полученный график функции « y(x) = −2x + 1 » это бесконечное множество точек, которые лежат на одной прямой.
При многократном увеличении графика функции мы увидим, что в самом деле вся прямая состоит из рядом стоящих точек.
Точки располагаются максимально близко к друг другу, поэтому по расчетам получается, что графиком функции будет являться прямая.
Функция (в математике)
Функция (в математике) — зависимость между двумя или большим количеством величин, при которой каждым значениям одних величин, называемых аргументами функции, ставятся в соответствие значения других величин, называемых значениями функции.
Например, функция сложения двух чисел ставит в соответствие слагаемым их сумму, то есть, к примеру, паре чисел 2 и 3 ставит в соответствие число 5.
Наиболее часто применяющиеся в математике функции относятся к так называемым однозначным функциям, то есть, каждому конкретному набору значений аргументов ставится в соответствие только одно значение. Отсюда и происхождение термина.
Такова, например, функция сложения двух чисел.
Каждая функция выражает некую закономерность, или даже закон, свойственную природе и проявляющуюся через измеряемые величины.
Например, Второй закон Ньютона выражается в виде функции
и дает нам значение ускорения, которое получит тело массы m, если к нему приложить силу F.
Это закон природы, все тела во Вселенной подчиняются ему! А выражается он такой простой функцией.
Когда какая-то величина зависит от других величин, говорят, что она является их функцией. Например, в случае закона Ньютона, ускорение является функцией массы и силы.
В зависимости от количества аргументов, от которого зависит функция, она может быть одно- или много- местной. Одноместная функция зависит от одного аргумента. Двухместная функция зависит от двух аргументов (таковы рассмотренные в этой статье функции) и так далее.
определена только для целых положительных значений x. При
определена для вещественных или комплексных значений x, модули которых меньше единицы. Ф. вида
Определение функции
Определение функции
Сложные функции
Действительные функции
В математическом анализе большую роль играют числовые функции.
Числовая функция – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция – это функция, значениями которой являются действительные числа.
Максимум и минимум
Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.
Верхняя и нижняя грани
Монотонные функции
Многозначные функции
Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.
Многозначная функция – это совокупность функций, определенных на некотором множестве.
Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.
Однозначная функция – это функция.
Сужение и продолжение функции
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.