Что называется действительной частью комплексного числа

Введение в комлексные числа

Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.

А школьники могут что-то новое узнать 😉
// Всех кого заинтересовал прошу под кат.

Итак, комплексные числа эта такие числа, которые можно записать как

Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство

x называется действительной частью, y — мнимой.

Это алгебраическая форма записи комплексного числа.

Существует также тригонометрическая форма записи комплексного числа z:

С введением, пожалуй, все.

Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.

У нас есть два таких комплексных числа:

Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:

Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число

Умножение выполняется вот так:

Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:

Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:

Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.

UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 😉

Источник

Что называется действительной частью комплексного числа

где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы

Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Числа z = x + iy и называются комплексно сопряженными.

Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.

Модуль r и аргумент φ можно рассматривать как полярные координаты вектора , изображающего комплексное число z = x + iy (см. рис. 7.1). Тогда из соотно­шений сторон в прямоугольном треугольнике получа­ем

Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле

Аргумент определяется из формул:

Используя формулу Эйлера

комплексное число можно записать в так назы­ваемой показательной (или экспоненциальной) форме

где r =| z | — модуль комплексного числа, а угол ( k =0;–1;1;–2;2…).

Пример 7.1. Записать комплексные числа в тригонометрической и показательной формах.

На множестве комплексны х чисел определен ряд операций.

Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,

Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:

(7.13) называется первой формулой Муавра.

Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:

На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби на число, сопряженное знаменателю, с дальнейшим применением равенства i 2 = –1 и формулы разности квадратов.

Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:

Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.

Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:

Пользуясь формулой (7.11), вычислим их произведение

На основании формулы (7.14) вычислим их частное

Решение. Используя (7.4) и (7.5), получаем:

Аналогично, для z ₂ можно записать:

По формулам (7.12) и (7.16) получим в тригонометрической форме:

Пользуясь формулами (7.14) и (7.17), получим в показательной форме:

в натуральную степень, определенному ранее формулой (7.13).

(7.18) называется второй формулой Муавра.

Пример 7.4. Найти все корни уравнения z 4 +16=0.

Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами

Приведем еще одну теорему, имеющую место над множеством комплексных чисел.

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.

Источник

Что такое комплексные числа

Первый урок по комплексным числам. Сегодня мы разберём:

Если же вас интересует тригонометрическая форма записи комплексного числа, либо извлечение корней из комплексных чисел — этим темам посвящены отдельные уроки.

Сегодня — лишь самое главное. Но не самое простое.:)

0. Краткая вводная

Когда-то нам хватало натуральных чисел:

Всё было прекрасно: «У тебя 5 бананов, у меня ещё 3 — итого у нас 5 + 3 = 8 бананов». Сумма двух натуральных чисел всегда даёт новое натуральное число (говорят, что операция сложения замкнута на множестве натуральных чисел).

Но вот на сцену выходит вычитание — и натуральных чисел стало недостаточно. Например разность 3 − 5 = −2 уже не будет натуральным. Так появились целые числа (натуральные, им противоположные и ноль):

Дальше к делу подключились операции умножения и деления. Да, произведение двух целых чисел всё ещё целое, но вот деление приводит к образованию дробей. Например, 1 : 2 или 5 : 4 уже нельзя записать целым числом. Так появилось множество рациональных чисел или множество дробей:

Это был настоящий триумф для древней математики, и в тот момент казалось, что ничего больше уже изобрести нельзя. Да и зачем?

Проблема пришла откуда не ждали. В какой-то момент классическое умножение «разрослось» до возведения в степень:

Тут-то и выяснилось, что возведение рационального числа в натуральную степень всё ещё будет рациональным числом. Но вот обратная операция — извлечение корня — выносит нас за пределы рациональных чисел:

\[\sqrt<2>=1,41421. \notin \mathbb\]

Так появилось множество действительных чисел — множество бесконечных десятичных дробей, которые могут быть периодическими (и тогда это обычное рациональное число) и непериодическими (такие числа называют иррациональными, и их неизмеримо больше).

Казалось бы: ну вот теперь точно всё! Что ещё нужно для счастья? Проблема в том, что на множестве действительных чисел нельзя извлечь даже самый простой квадратный корень из отрицательного числа:

Однако законы физики (особенно электродинамика и вообще всё, где есть слово «динамика») как бы намекали, что множество содержательных процессов протекает там, где привычные корни не извлекаются. А значит, следует расширить множество действительных чисел так, чтобы такие корни всё же извлекать.

И тут открылись врата в Ад.

1. Комплексная единица

Начнём с ключевого определения.

Однако в остальном это такое же число, как и все остальные. Комплексные единицы можно складывать, умножать, их можно комбинировать с «нормальными» числами:

2. Стандартная форма записи комплексных чисел

А теперь всё по-взрослому.

Определение. Комплексное число — это любое число вида

\[\begin & z=5+3i \\ & \operatorname\left( z \right)=5 \\ & \operatorname\left( z \right)=3 \\ \end\]

\[\begin & 5=5+0\cdot i \\ & x=x+0\cdot i\left( \forall x\in \mathbb \right) \\ \end\]

И напротив: существуют «чисто мнимые» числа, у которых вообще нет действительной части. Та же комплексная единица, например:

\[\begin i &=0+1\cdot i \\ 35i &=0+35\cdot i \\ \end\]

Таким образом, действительные числа являются частным случаем комплексных. Подобно тому как рациональные числа являются частным случаем действительных (в конце концов, рациональные числа — те же десятичные дроби, но с дополнительным условием: они периодические).

2.1. Равенство комплексных чисел

В самом деле, пусть некоторое число записано двумя способами:

Соберём все действительные слагаемые слева, а мнимые — справа:

Слева мы видим действительное число. Значит, справа тоже должно стоять действительное число. Единственная ситуация, в которой это возможно:

Получается, что справа от знака равенства стоит ноль. Следовательно, слева тоже ноль:

Следовательно, исходные записи совпадают.

Поэтому имеет смысл следующее определение.

Определение. Два комплексных числа равны друг другу тогда и только тогда, когда равны их действительные части, а также равны их мнимые части:

Если хотя бы одна из частей не равна, то и сами числа не равны.

Поскольку от перестановки слагаемых сумма не меняется (сложение чисел — настолько суровая операция, что какие-то там «комплексные единицы» никак не нарушают его коммутативности), мы можем записать:

А вот перестановка мнимой и действительной части (если эти части разные) немедленно ведёт к нарушению равенства:

К координатной плоскости мы ещё вернёмся. А пока определим правила сложения и вычитания комплексных чисел.

3. Сложение и вычитание комплексных чисел

Выше мы проводили аналогию между комплексными числами и многочленами. Идём по этому пути дальше и вспоминаем, что многочлены можно складывать, группируя слагаемые и приводя подобные:

Точно так же можно определить и сложение (да и вычитание) двух комплексных чисел. Всё просто:

Другими словами, при сложении комплексных чисел отдельно складываются их действительные части и отдельно — мнимые. То же самое для вычитания.

Не нужно учить эти формулы. Дальше будут формулы умножения и деления — они ещё сложнее. Нужно понять ключевую идею: мы работаем с комплексными числами точно так же, как с многочленами. С небольшим дополнением: все степени комплексной единицы выше первой «сжигаются» прямо по определению самой единицы:

Небольшое замечание. В отличие от математики 5—6 классов, в серьёзной «взрослой» алгебре нет такого понятия как «вычитание». Зато есть понятие противоположного элемента и алгебраической суммы:

Всё это в полной мере относится и к комплексным числам. Там тоже есть противоположные:

Есть ноль (нейтральный элемент по сложению):

\[\begin 0 & =0+0\cdot i \\ z & =a+bi \\ z+0 & =\left( a+0 \right)+\left( b+0 \right)\cdot i= \\ & =a+bi=z \end\]

В общем, множество комплексных чисел — это абсолютно «нормальное» множество с понятной операцией сложения. Буквально через пару минут мы определим и умножение, но сначала давайте всё-таки запишем определение самого множества комплексных чисел.

Записывается это так:

Не пугайтесь, когда увидите подобную запись где-нибудь в учебнике алгебры. По сути, это краткая запись всего того, о чём мы говорили выше. Ничего нового мы здесь не узнали.

А вот что действительно представляет интерес — сейчас узнаем.:)

4. Геометрическая интерпретация комплексных чисел

Такие упорядоченные пары удобно рассматривать как координаты точек. По горизонтали (ось абсцисс) мы будем отмечать действительную часть числа, а по вертикали (ось ординат) — мнимую.

Определение. Комплексная плоскость — декартова система координат, где по горизонтали отмечается действительная часть комплексного числа, а по вертикали — мнимая.

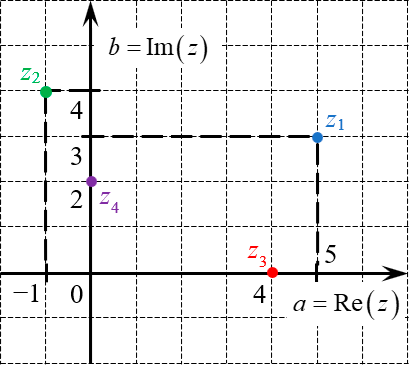
Рассмотрим несколько примеров. Отметим на комплексной плоскости числа:

4.1. Ещё раз о сложении и вычитании

Такое представление чисел — в виде точек на комплексной плоскости — называется геометрической интерпретацией. Числа в таком виде удобно складывать и вычитать. По сути, всё сводится к сложению обычных векторов.

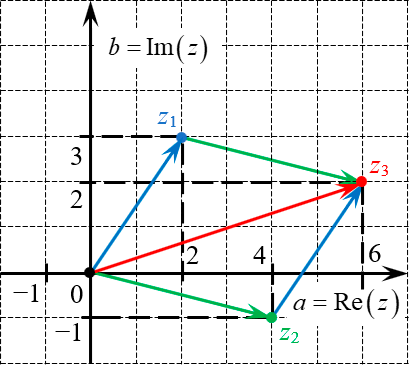
Допустим, мы хотим сложить два числа:

Отметим эти числа на комплексной плоскости, построим векторы из начала координат с концами в отмеченных точках, а затем просто сложим эти векторы (по правилу треугольника или параллелограмма — как пожелаете):

Координаты новой точки: (6; 2). Следовательно, сумма равна:

Аналогичный результат можно получить и алгебраически:

Как видим, алгебраические выкладки заняли гораздо меньше времени и места. Уже хотя бы потому что не потребовалось чертить систему координат.:)

Зачем же тогда нужна комплексная плоскость и геометрическая интерпретация? Всё встанет на свои места буквально через пару уроков, когда мы рассмотрим тригонометрическую форму записи комплексных чисел, а также будем извлекать из этих чисел корни.

А чтобы подготовиться к этим урокам, рассмотрим ещё два ключевых определения.

5. Комплексно-сопряжённые и модуль числа

Для начала вспомним школьную алгебру. Работа с многочленами, 7-й класс:

называется разностью квадратов и является одной из формул сокращённого умножения.

В математических классах с помощью сопряжённых искали обратные числа, чтобы затем решать сложные показательные и логарифмические уравнения:

Теперь настало время комплексных чисел. В них тоже можно ввести понятие сопряжённых.

5.1. Комплексно-сопряжённые

Комплексно-сопряжённые числа отмечаются чертой сверху.

Рассмотрим несколько примеров:

Видим, что комплексно-сопряжённое к «чисто мнимому» числу есть число, ему противоположное. А комплексно-сопряжённое к действительному числу есть само это число.

Зачем нужны комплексно-сопряжённые? Вспомним всё ту же формулу разности квадратов:

Итак, произведение числа на комплексно-сопряжённое даёт сумму квадратов действительной и мнимой части. Это ключевое свойство комплексно-сопряжённых, и оно позволяет нам рассмотреть следующее определение.

5.2. Модуль комплексного числа

Снова вспомним школьную алгебру. Модуль действительного числа определяют так:

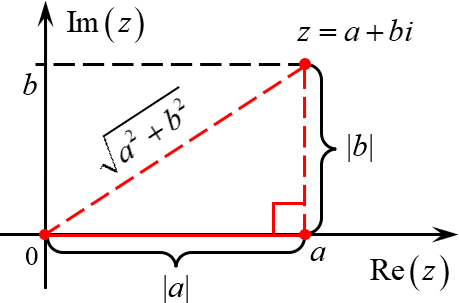
Ключевая идея: модуль числа — это всегда неотрицательная величина, равная расстоянию от точки, соответствующей этому числу, до начала отсчёта. Но всё это происходит на числовой прямой. На комплексной плоскости к делу подключается теорема Пифагора.

Вновь обратимся к геометрической интерпретации:

\[b=0\Rightarrow \left| z \right|=\sqrt<<^<2>>>\]

Получается, что на множестве комплексных чисел нельзя ввести привычные нам понятия «больше» или «меньше». Поскольку каждое число характеризуется двумя независимыми параметрами (действительной и мнимой частью), нет универсальной меры, нет отношения порядка.

Можно считать это фундаментальным законом природы. Когда мы держим в голове больше одного параметра, нет больше универсального критерия успеха:

Оценка одного и того же события будет меняться в зависимости от настроения и наших предпочтений.

Модуль числа нам пригодится в следующем уроке. А вот комплексно-сопряжённые мы будем применять уже сейчас.

6. Умножение и деление комплексных чисел

Комплексные числа можно не только складывать и вычитать, но даже умножать и делить друг на друга.

6.1. Умножение

С умножением ничего особенного.

\[\begin <_<1>>\cdot <_<2>> & =\left( a+bi \right)\left( c+di \right)= \\ & =ac+bc\cdot i+ad\cdot i+bd\cdot <^<2>>= \\ & =\left( ac-bd \right)+\left( ad+bc \right)\cdot i\end\]

Как видим, произведение комплексных чисел вновь даёт комплексное число.

Как и в случае со сложением, не нужно учить эти формулы наизусть. Лучше просто потренироваться и понять сам механизм:

Достаточно решить 10—15 таких примеров — и никакие специальные формулы и определения вам больше не понадобятся. То же самое и с делением.

6.2. Деление

Финальный бросок — попробуем разделить одно комплексное число на другое. Разумеется, делитель не должен быть нулём, иначе частное не определено.

Частное комплексных чисел вновь будет комплексным числом.

Саму формулу не нужно запоминать. Достаточно лишь отметить для себя, что мы умножили числитель и знаменатель дроби на комплексно-сопряжённое к знаменателю. Само деление можно выполнять напролом:

Тем не менее, даже после основательной тренировки умножение и особенно деление комплексных чисел остаётся трудоёмкой операцией, где можно допустить множество ошибок. Поэтому для таких операций (а также для кое-чего гораздо более серьёзного) математики придумали другую форму записи комплексных чисел — тригонометрическую. С ней мы и познакомимся на следующем уроке.:)

Источник

Комплексные числа

Известно, что квадратное уравнение с вещественными коэффициентами и отрицательным дискриминантом не имеет вещественных корней. В частности, уравнение
$$
z^2+1=0\nonumber
$$
не имеет корней на множестве \(\mathbb\). Возникает потребность расширить множество \(\mathbb\) так, чтобы на более широком множестве было разрешимо квадратное уравнение с любыми вещественными коэффициентами.

Определение комплексного числа.

Комплексными числами называют пары \((x,y)\) вещественных (действительных) чисел \(x\) и \(y\), для которых следующим образом определены понятие равенства и операции сложения и умножения.
Обозначим комплексное число \((x,y)\) буквой \(z\), то есть положим \(z=(x,y)\). Пусть \(z_1=(x_1,y_1)\), \(z_2=(x_2,y_2)\). Два комплексных числа \(z_1\) и \(z_2\) считаются равными тогда и только тогда, когда \(x_1=x_2\) и \(y_1=y_2\), то есть
$$
\<(x_1,y_1) = (x_2,y_2)\>\Leftrightarrow \\ \wedge\ \.\nonumber
$$

Сумма и произведение комплексных чисел \(z_1\) и \(z_2\) обозначаются соответственно \(z_1+z_2\) и \(z_1z_2\) и определяются формулами
$$
z_1+z_2=(x_1+x_2,y_1+y_2),\label
$$
$$
z_1z_2=(x_1x_2-y_1y_2,x_1y_2+x_2y_1).\label
$$

Из формул \eqref и \eqref следуют соотношения
$$
(x_1,0) + (x_2,0) = (x_1+x_2,0),\qquad (x_1,0)(x_2,0) = (x_1x_2,0),\nonumber
$$
которые показывают, что операции над комплексными числами вида \((x, 0)\) совпадают с операциями над действительными числами. Поэтому комплексное число вида \((x, 0)\) отождествляют с действительным числом \(x\), то есть полагают \((x,0) = x\).

Следовательно, любое комплексное число \(z= (x,y)\) можно записать в виде \(x + iy\), то есть
$$
z = x + iy.\label
$$

Запись комплексного числа \(z = (x,y)\) в виде \eqref называют алгебраической формой комплексного числа.

В записи \eqref число \(x\) называют действительной частью комплексного числа и обозначают \(Re\ z\), а число \(y\) — мнимой частью и обозначают \(Im\ z\), то есть
$$
Re\ z = x,\quad Im\ z = y. \nonumber
$$

Если \(x= 0\), то есть \(z = iy\), то такое комплексное число называют чисто мнимым.

Здесь и всюду в дальнейшем, если не оговорено противное, в записи \(x+iy\) числа \(x\) и \(y\) считаются действительными (вещественными).

Число \(\displaystyle\sqrt\) обозначают \(|z|\) и называют модулем комплексного числа \(z\), то есть
$$
|z|=|x + iy|=\sqrt.\label
$$
Заметим, что \(|z|\geq 0\) и \(\<|z| = 0\>\Leftrightarrow \\).

Комплексное число \(x-iy\) называют сопряженным комплексному числу \(z = x + iy\) и обозначают \(\overline\) то есть
$$
\overline = \overline= x-iy.\label
$$
Из равенств \eqref и \eqref следует, что
$$
|z| = |\overline|,\qquad z\overline=|z|^2,\label
$$
так как \(z\overline=(x+iy)(x-iy) = x^2 + y^2\).

Свойства операций.

Операции сложения и умножения комплексных чисел обладают свойствами:

Эти свойства вытекают из определения операций сложения и умножения комплексных чисел и свойств операций для вещественных чисел.

Из уравнения \eqref в силу правила равенства и определения суммы комплексных чисел следует, что
$$
z_1-z_2=(x_1-x_2)+i(y_1-y_2).\nonumber
$$

Деление на множестве \(\mathbb\) вводится как операция, обратная умножению, а частным от деления комплексного числа \(z_1=_1+iy_1\) на число \(z_2 = x_2 + iy_2\) называют такое число \(z\), которое удовлетворяет уравнению
$$
zz_2=z_1\label
$$
и обозначается \(z_1:z_2\) или \(\displaystyle \frac\).

Докажем, что уравнение \eqref для любых комплексных чисел \(z_1\) и \(z_2\), где \(z_2\neq 0\), имеет единственный корень.

\(\circ\) Умножая обе части уравнения \eqref на \(\overline_2\), получим в силу равенства \eqref уравнение
$$
z|z_2|^2 = z_1\overline_2,\label
$$
которое равносильно уравнению \eqref, так как \(\overline_2\neq 0\).

Эту формулу можно не запоминать — важно знать, что она получается умножением числителя и знаменателя на число, сопряженное со знаменателем.

Найти частное \(\displaystyle \frac\), если \(z_1=5-2i,\ z_2=3 + 4i\).

Источник