Что называется аргументом комплексного числа аргументом

Комплексные числа

Алгебраическая форма записи комплексных чисел

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Деление комплексных чисел, записанных в алгебраической форме

Изображение комплексных чисел радиус-векторами на координатной плоскости

Аргумент комплексного числа

Тригонометрическая форма записи комплексного числа

Формула Эйлера. Экспоненциальная форма записи комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Извлечение корня натуральной степени из комплексного числа

Алгебраическая форма записи комплексных чисел

Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле

Для произвольного комплексного числа z справедливо равенство:

а для произвольных комплексных чисел z₁ и z₂ справедливы неравенства:

Деление комплексных чисел, записанных в алгебраической форме

Деление комплексного числа z₁ = x₁ + i y₁ на отличное от нуля комплексное число z₂ = x₂ + i y₂ осуществляется по формуле

Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:

Деление на нуль запрещено.

Изображение комплексных чисел радиус-векторами координатной плоскости

Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Аргумент комплексного числа

Считается, что комплексное число нуль аргумента не имеет.

Тогда оказывается справедливым равенство:

(3)

(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.

Таблица 1. – Формулы для определения аргумента числа z = x + i y

y z

Расположение числа z	Знаки x и y	Главное значение аргумента	Аргумент	Примеры
Положительная вещественная полуось
Положительная мнимая полуось
Второй квадрант
Отрицательная вещественная полуось	Положительная вещественная полуось
Знаки x и y
Главное значение аргумента	0
Аргумент	φ = 2kπ
Примеры

Главное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримеры

x zТретий
квадрантЗнаки x и y

x zОтрицательная
мнимая
полуосьЗнаки x и y

y zЧетвёртый
квадрантЗнаки x и y

Положительная вещественная полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Положительная мнимая полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Отрицательная вещественная полуось

Отрицательная мнимая полуось

x z = x + i y может быть записано в виде

Формула Эйлера. Экспоненциальная форма записи комплексного числа

В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :

Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде

Из формулы (7) вытекают, в частности, следующие равенства:

а из формул (4) и (6) следует, что модуль комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

Действительно, умножение и деление двух произвольных комплексных чисел и записанных в экспоненциальной форме, осуществляется по формулам

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле

Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Извлечение корня натуральной степени из комплексного числа

Пусть — произвольное комплексное число, отличное от нуля.

Для того, чтобы решить уравнение (8), перепишем его в виде

следствием которых являются равенства

(9)

Из формул (9) вытекает, что уравнение (8) имеет n различных корней

(10)

то по формуле (10) получаем:

Источник

Модуль и аргумент комплексного числа

Пример №1 Найти модуль и аргумент числа и представить число в тригонометрической и показательной формах.

, поэтому прибавляем и берем , то есть то что нужно.

Кроме алгебраической формы записи комплексного числа имеются тригонометрическая и показательная формы записи. Модуль и аргумент числа нужны для остальных двух форм записи комплексных чисел. В тригонометрической форме записи число выглядит так:

а в показательной форме:

При переходе от показательной форме к тригонометрической используется формула Эйлера:

Зачем нужны три формы записи? Дело в том, что некоторые действия удобно производить с конкретно одной формой. Например, сложение удобно проводить с числами в алгебраической форме и неудобно с числами в двух других формах. Умножение и деление очень хорошо получается с числами в показательной и тригонометрической формах. Но одно важно: чтобы произвести арифметическое действие с комплексными числами нужно перевести их в одну форму. Приведем несколько примеров.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Источник

Модуль комплексного числа

Модуль комплексного числа

Модулем комплексного числа называется длина вектора, соответствующего этому числу: .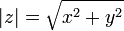
Модуль комплексного числа z обычно обозначается | z | или r.

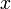
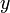
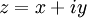
Пусть и — вещественные числа такие, что комплексное число (обычные обозначения). Тогда

Полезное

Смотреть что такое «Модуль комплексного числа» в других словарях:

модуль комплексного числа — kompleksinio skaičiaus modulis statusas T sritis fizika atitikmenys: angl. modulus of complex number vok. Betrag der komplexen Zahl, m rus. модуль комплексного числа, m pranc. module du nombre complexe, m … Fizikos terminų žodynas

МОДУЛЬ — (modulus) Величина числа с точки зрения его расстояния от 0. Модуль, или абсолютное значение реального числа х (обозначается |х|), является разностью между х и 0 независимо от знака. Следовательно, если х>0, то |х|=х и если х <0, то |х|=–х … Экономический словарь

МОДУЛЬ — комплексного числа см. Абсолютная величина. Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab … Большой Энциклопедический словарь

Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия

Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия

МОДУЛЬ — (в математике) мера для сравнения однородных величин и для выражения одной из них помощью другой; м. выражается числом. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. МОДУЛЬ (лат.). 1) число, которым множатся… … Словарь иностранных слов русского языка

МОДУЛЬ (в математике) — МОДУЛЬ комплексного числа, см. Абсолютная величина (см. АБСОЛЮТНАЯ ВЕЛИЧИНА). Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab … Энциклопедический словарь

Модуль — I Модуль (от лат. modulus мера) в архитектуре, условная единица, принимаемая для координации размеров частей здания или комплекса. В архитектуре разных народов в зависимости от особенностей строительной техники и композиции зданий за М.… … Большая советская энциклопедия

модуль — я; м. [от лат. modulus мера] 1. чего. Спец. Величина, характеризующая какое л. свойство твёрдого тела. М. сжатия. М. упругости. 2. Матем. Действительное число, абсолютная величина отрицательного или положительного числа. М. комплексного числа. М … Энциклопедический словарь

Источник

Что называется аргументом комплексного числа аргументом

VII .1. Формы записи комплексных чисел и действия над ними

где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы

Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Числа z = x + iy и называются комплексно сопряженными.

Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.

Модуль r и аргумент φ можно рассматривать как полярные координаты вектора , изображающего комплексное число z = x + iy (см. рис. 7.1). Тогда из соотно­шений сторон в прямоугольном треугольнике получа­ем

Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле

Аргумент определяется из формул:

Используя формулу Эйлера

комплексное число можно записать в так назы­ваемой показательной (или экспоненциальной) форме

где r =| z | — модуль комплексного числа, а угол ( k =0;–1;1;–2;2…).

Пример 7.1. Записать комплексные числа в тригонометрической и показательной формах.

На множестве комплексны х чисел определен ряд операций.

Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,

Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:

(7.13) называется первой формулой Муавра.

Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:

На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби на число, сопряженное знаменателю, с дальнейшим применением равенства i 2 = –1 и формулы разности квадратов.

Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:

Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.

Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:

Пользуясь формулой (7.11), вычислим их произведение

На основании формулы (7.14) вычислим их частное

Решение. Используя (7.4) и (7.5), получаем:

Аналогично, для z ₂ можно записать:

По формулам (7.12) и (7.16) получим в тригонометрической форме:

Пользуясь формулами (7.14) и (7.17), получим в показательной форме:

в натуральную степень, определенному ранее формулой (7.13).

(7.18) называется второй формулой Муавра.

Пример 7.4. Найти все корни уравнения z 4 +16=0.

Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами

Приведем еще одну теорему, имеющую место над множеством комплексных чисел.

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.

Источник