Что называется апертурой интерференции чем она определяется
Что называется апертурой интерференции чем она определяется
Световые волны когерентны, если они способны интерферировать. Оказывается, реальная световая волна не вполне когерентна сама себе. Две световые волны, полученные из одной методом деления амплитуды или методом деления волнового фронта, не обязательно интерферируют друг с другом. Есть две основные причины возможной некогерентности таких волн.
Квазимонохроматический свет.
Квазимонохроматический свет можно представить как суперпозицию монохроматических волн, частоты которых расположены в узком спектральном диапазоне.
При сложении двух волн с различающимися частотами интенсивность суммарного света равна сумме интенсивностей суммируемых волн, и в этом смысле волны разных частот не интерферируют друг с другом, если время усреднения в выражении для интенсивности устремить к бесконечности. При малом времени усреднения окажется, что волны разных частот интерферируют, но интерференционные полосы «бегут» по экрану, так что интенсивность света в каждой точке экрана гармонически осциллирует с частотой равной разности частот суммируемых волн. Такую интерференционную картину можно наблюдать при сложении излучения двух однотипных лазеров.
Если в задаче специально не оговорено время усреднения, то подразумевается, что оно бесконечно. В таком случае интенсивность в каждой точке экрана представляет собой сумму интенсивностей интерференционных картин монохроматических световых волн, составляющих квазимонохроматический свет. Правильный результат при решении задачи получится и в том случае, если считать, что частота света медленно «гуляет» в пределах ширины спектральной линии излучения, а интерференционная картина при этом «смазывается», так как положение полос меняется в зависимости от частоты света.
Если же полоса «бегает» заметно меньше, чем на ширину полос, то при усреднении по времени на фотопластине останутся четкие полосы.
На экране есть, или может быть, одна полоса, которая при изменении частоты света «не бегает» по экрану вовсе. Это светлая полоса, для которой оптическая разность хода равна нулю, так называемая нулевая полоса. Нулевая полоса «не смазывается» при любой спектральной ширине источника света, так как при нулевой разности хода для любой частоты света интерферирующие волны окажутся в одинаковой фазе и дадут светлую полосу.
Если одна из интерферирующих волн по дороге от источника света испытала отражение с потерей полуволны, то нулевая полоса будет темной.
Таким образом, при интерференции квазимонохроматического света на экране одна часть интерференционной картины «смазывается», другая остается с высоким контрастом (видностью) полос. Поэтому в задачах на тему «Интерференция квазимонохроматического света» часто ставится вопрос определения области на экране, где интерференционная картина «не смазывается». Либо по известным размерам этой области требуется найти параметры задачи, от которых эта область зависит. При рассмотрении этой области удобно использовать понятие «порядок интерференции».
Порядок интерференции.
Если порядок интерференции шумит на единицу ( ), то на единицу шумит и номер интерференционной полосы для выбранной точки экрана. Этому соответствует шумовое перемещение интерференционной картины на расстояние равное ширине полосы. При таком перемещении интерференционная картина полностью «смазывается». Найдем теперь, какое изменение частоты и длины волны света соответствует изменению порядка интерференции на единицу.
Область высокой видности интерференционной картины при квазимонохроматическом источнике света.
Из равенства с учетом получаем два новых условия границы «несмазанной» области интерференционной картины:
определяет границу области экрана, в которой хорошо различимы интерференционные полосы.
Временная когерентность.
Временная когерентность связана с когерентностью вдоль луча.
Эта формула часто используется при решении задач.
Подчеркнем, что условие «разность фаз шумит больше, чем на » не следует путать с условием «разность фаз больше, чем «.
Пространственная когерентность.
Видность интерференционной картины с протяженным источником света.
Будем считать, что источник света представляет собой полоску постоянной ширины и яркости.
Связь пространственной когерентности и углового размера источника света.
Перепишем теперь формулу для размера источника в виде
Апертура интерференции.
Перепишем последнюю формулу еще в одном виде
означает, что максимальная апертура интерференции равна отношению длины волны к размеру источника света. Если апертура больше, то нет интерференции.
Объем когерентности.
Рассмотрим две точки, через которые проходит свет. Если проекции этих точек на направление светового луча удалены друг от друга меньше, чем на длину продольной когерентности, и если их проекции на плоскость перпендикулярную лучу удалены друг от друга меньше, чем на радиус поперечной когерентности, то данные две точки принадлежат одному объему когерентности.
Рассмотрим еще раз схему опыта Юнга и проследим перемещение объема когерентности вдоль лучей.
После щелей получаются два объема одной когерентности, рис. 26в.
Совместное влияние временной и пространственной когерентности на интерференционную картину.
При равных интенсивностях интерферирующих волн зависимость видности интерференционной картины от номера полосы позволяет оценить порознь пространственную и временную когерентность света в месте расположения вторичных источников интерферирующего света, или оценить размер и немонохроматичность источника света.
Видность вблизи нулевой полосы определяется только пространственной когерентностью, а изменение видности с номером полосы определяется только временной когерентностью источника света.
Локализация интерференционной картины.
Интерференция света, отраженного от тонкой прозрачной пленки, является важным частным случаем получения интерференционной картины методом деления амплитуды. В случае протяженного источника света интерференционная картина может быть получена либо очень близко к поверхности пленки, либо очень далеко от пленки, как говорят, на бесконечности. Соответственно говорят об интерференционной картине локализованной на поверхности пленки и на бесконечности. Как показывает опыт, в промежуточных положениях экрана интерференционная картина оказывается размытой.
Удаленный объект отображается собирающей линзой в ее фокальной плоскости. Оказывается, интерференционную картину, локализованную на бесконечности, можно также наблюдать в фокальной плоскости линзы.
Линза позволяет наблюдать и кольца Ньютона локализованные в плоскости между плоской поверхностью стекла и соприкасающейся с ней выпуклой поверхностью линзы. Если экран физически поставить между соприкасающимися поверхностями, то до одной из них свет просто не дойдет, и интерференции не будет.
Линза отображает локализованную в плоскости касания интерференционную картину в виде колец Ньютона на экран по законам геометрической оптики:
Интерферируют те лучи, которые выходят из одной точки источника и попадают в одну точку плоскости локализации интерференционной картины. Не важно, что в этой плоскости нет экрана, и неважно, что после плоскости лучи расходятся. Линза собирает их на экране с той же разностью фаз, которую они имели в плоскости локализации интерференционной картины. Поэтому светлая полоса изображается в светлую, а темная в темную.
Есть, правда, некоторое отличие между наблюдением интерференционной картины на экране и интерференционной картины локализованной в пространстве.
На экране интерференционную картину можно рассматривать с разных сторон. Для наблюдения интерференционной картины локализованной в пространстве линзу окуляра (или глаз) можно поставить только по ходу лучей, причем через линзу должны проходить оба интерферирующих луча, как, например, на рис. 27. Если через линзу проходит только один из интерферирующих лучей (рис. 28), то изображения интерференционной картины не будет. Вместо полос будет серый фон освещения одним лучом.
Полосы равной толщины и полосы равного наклона.
Полосы равной толщины и равного наклона наблюдаются при интерференции волн, отраженных от двух границ прозрачной пленки или плоскопараллельной пластинки.
Полосы равного наклона локализованы на бесконечности.
Полосы равной толщины локализованы в плоскости отражающей пленки. В пределах ширины пленки можно считать, что интерференционная картина локализована там, где вам удобнее.
Методические указания к практическим занятиям по курсу общей физики
Главная > Методические указания
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Временная когерентность связана с когерентностью вдоль луча. Когерентность — это способность к интерференции. Рассмотрим две точки на одном луче как два возможных вторичных источника света для наблюдения интерференционной картины. При этом расстояние от каждой из точек до мысленного экрана предполагается одинаковым.
Возможный вариант оптической схемы приведен на рис. 23. Здесь A и B — две выбранные вдоль луча точки, в которые мысленно поместим полупрозрачные пластинки для получения интерференционной картины на экране C. По условию задачи AC = BC.
L || = 
Эта формула часто используется при решении задач.
Наряду с понятием «продольная когерентность», используется близкое ему понятие «временная когерентность». Фаза светового поля в точке A (см. рис. 23) в момент времени t равна фазе поля в точке B в момент t+, где — время распространения света от A до B. Следовательно, когерентность поля в точках A и B в один момент времени t точно такая же, как когерентность в одной точке B, но в два разных момента времени t и t+.
= L || 







Можно посмотреть на когерентность светового поля в точках A и B несколько иначе. Длина волны шумит. Следовательно, шумит число длин волн, которое укладывается на отрезке AB. Пропорционально шумит разность фаз в точках A и B. Результат интерференции зависит от разности фаз. Если разность фаз в точках A и B шумит больше, чем на 2, то поле в этих точках некогерентно, если меньше, то поле когерентно. В такой форме условие когерентности поля в точках A и B не требует расположения этих точек вдоль луча или рассмотрения поля в них в один момент времени.
Подчеркнем, что условие «разность фаз шумит больше, чем на 2» не следует путать с условием «разность фаз больше, чем 2».
Пространственная когерентность — это когерентность света в направлении, перпендикулярном лучу (поперек луча). Получается, что это когерентность разных точек поверхности равной фазы. Но на поверхности равной фазы разность фаз равна нулю и, казалось бы, не шумит. Это не совсем так. Реальный источник света не точечный, поэтому поверхность равных фаз испытывает шумовые повороты, оставаясь в каждый момент времени перпендикулярной направлению на излучающий в данный момент точечный источник света, расположенный в пределах реального источника света. Повороты поверхности равной фазы вызваны тем, что свет в точку наблюдения приходит то от одной, то от другой точки источника.
Видность интерференционной картины
с протяженным источником света
Рассмотрим оптическую схему опыта Юнга (рис. 24). Если источник света не точечный и имеет размер b поперек луча, то интерференционная картина несколько «смазывается», потому что каждый точечный источник, из которых состоит источник света, дает свою интерференционную картину, и эти картины несколько сдвинуты друг относительно друга.
Будем считать, что источник света представляет собой полоску постоянной ширины и яркости. Картина полностью «смажется», если интерференционные картины от крайних точек источника будут сдвинуты относительно друг друга ровно на одну полосу интерференции, что соответствует изменению разности хода на одну длину волны .
Из рис. 24 видно, что при переходе от одной точки источника света к другой разность хода может измениться только слева от экрана с двумя щелями. Выясним, какому перемещению b точечного источника на рис. 24 соответствует изменение разности хода на .
b = 
при котором интерференционные полосы полностью «смажутся».
Связь пространственной когерентности и
углового размера источника света
Если интерференционная картина на экране (см. рис. 24) «смазывается» при размере источника b, то L 2 — размер поперечной когерентности света в месте расположения экрана с двумя щелями. Действительно, две щели — это две точки на фронте волны, которые являются вторичными источниками света. Интерференционная картина пропадает, если вторичные источники света некогерентны. Они некогерентны, если расположены на расстоянии, большем или равном длине пространственной когерентности.
Перепишем теперь формулу для размера источника в виде соотношения


Перепишем последнюю формулу в следующем виде:


=
означает, что максимальная апертура интерференции равна отношению длины волны к размеру источника света. Если апертура больше, то нет интерференции. Свет из источника размером b выходит когерентно в любой угол /b.
Рассмотрим две точки, через которые проходит свет. Если проекции этих точек на направление светового луча удалены друг от друга меньше, чем на длину продольной когерентности, и если их проекции на плоскость, перпендикулярную лучу, удалены друг от друга меньше, чем на радиус поперечной когерентности, то данные две точки принадлежат одному объему когерентности.
Рассмотрим еще раз схему опыта Юнга и проследим перемещение объема когерентности вдоль лучей.
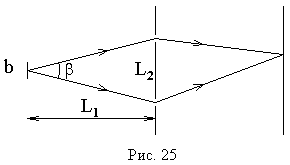
Сначала объем когерентности «распространяется» из источника света в угол /b (рис. 25,а).
Затем края этого объема «просачиваются» через две щели (рис. 25,б). Если объем когерентности не накрывает сразу обе щели, то не будет интерференционной картины на экране, так как в этом случае недостаточна пространственная когерентность на фронте, проходящем через две щели, и щели как вторичные источники света некогерентны.
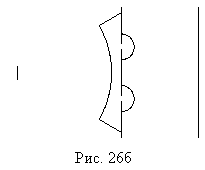
После щелей получаются два объема одной когерентности (рис. 25,в).
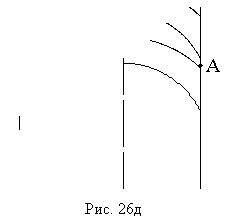
Эти два объема приходят в интересующую нас точку A экрана либо почти одновременно, заметно перекрываясь, как на рис.25,г, либо приходят по очереди, как на рис. 25,д. В первом случае в данной точке экрана интерференционная картина «не смазана», а во втором — «смазана». В этих двух вариантах видность картины определяется временной когерентностью, длиной объема когерентности вдоль луча.
Интерференция двух волн возможна тогда и только тогда, когда свет, пройдя двумя путями, попадает на экран так, что объем когерентности перекрывается сам с собой. Чем больше он перекрывается, тем больше видность интерференционной картины.
Совместное влияние временной и пространственной когерентности
на интерференционную картину
При равных интенсивностях интерферирующих волн зависимость видности интерференционной картины от номера полосы позволяет оценить порознь пространственную и временную когерентность света в месте расположения вторичных источников интерферирующего света или оценить размер и немонохроматичность источника света.
Видность вблизи нулевой полосы определяется только пространственной когерентностью, а изменение видности с номером полосы определяется временной когерентностью источника света.
Локализация интерференционной картины
Интерференция света, отраженного от тонкой прозрачной пленки, является важным частным случаем получения интерференционной картины методом деления амплитуды. В случае протяженного источника света интерференционная картина может быть получена либо очень близко к поверхности пленки, либо очень далеко от пленки, как говорят, на бесконечности. Соответственно говорят об интерференционной картине локализованной на поверхности пленки и на бесконечности. Как показывает опыт, в промежуточных положениях экрана интерференционная картина оказывается размытой.
Удаленный объект отображается собирающей линзой в ее фокальной плоскости. Оказывается, интерференционную картину, локализованную на бесконечности, можно также наблюдать в фокальной плоскости линзы.
Линза позволяет наблюдать и кольца Ньютона, локализованные в плоскости между плоской поверхностью стекла и соприкасающейся с ней выпуклой поверхностью линзы. Если экран физически поставить между соприкасающимися поверхностями, то до одной из них свет просто не дойдет, и интерференции не будет.
Линза отображает локализованную в плоскости касания интерференционную картину в виде колец Ньютона на экран по законам геометрической оптики:



Здесь f — фокусное расстояние линзы, a — расстояние от плоскости локализации интерференционной картины до линзы, b — расстояние от линзы до изображения интерференционной картины на экране. Интерференционная картина в плоскости локализации играет роль светящегося тела.
Интерферируют те лучи, которые выходят из одной точки источника и попадают в одну точку плоскости локализации интерференционной картины. Неважно, что в этой плоскости нет экрана, и что после плоскости лучи расходятся. Линза собирает их на экране с той же разностью фаз, которую они имели в плоскости локализации интерференционной картины. Поэтому светлая полоса изображается в светлую, а темная в темную.
Интерференционную картину можно наблюдать вообще без экрана. При этом хрусталик глаза играет роль линзы, а сетчатка — роль экрана. Интерференционную картину, локализованную на бесконечности, можно рассматривать в подзорную трубу, а локализованную в другой плоскости можно рассматривать через окуляр, как рассматривают близко расположенные мелкие предметы.
Есть, правда, некоторое отличие между наблюдением интерференционной картины на экране и интерференционной картины локализованной в пространстве.
На экране интерференционную картину можно рассматривать с разных сторон. Для наблюдения интерференционной картины, локализованной в пространстве, линзу окуляра (или глаз) можно поставить только по ходу лучей, причем через линзу должны проходить оба интерферирующих луча, как, например, на рис.26. Если через линзу проходит только один из интерферирующих лучей (рис. 27), то изображения интерференционной картины не будет. Вместо полос будет серый фон освещения одним лучом.
Полосы равной толщины и полосы равного наклона
Полосы равной толщины и равного наклона наблюдаются при интерференции волн, отраженных от двух границ прозрачной пленки или плоскопараллельной пластинки.
Полосы равного наклона локализованы на бесконечности.
Полосы равной толщины локализованы в плоскости, отражающей пленки. В пределах ширины пленки можно считать, что интерференционная картина локализована там, где вам удобнее.
Для наблюдения полос равной толщины отражающие поверхности не обязательно должны быть идеально плоскопараллельны. Пара отражающих плоскостей может образовывать тонкий клин. Могут быть соприкасающиеся поверхности, одна или обе из которых сферические (кольца Ньютона).
Более того, две отражающих поверхности могут быть расположены в разных местах, как в интерферометре Майкельсона (рис.28). Здесь S — источник света, P — экран для наблюдения интерференции отраженных волн от зеркал 1 и 2, 3 — полупрозрачная пластинка. Если зеркало 2 мысленно отразить в полупрозрачной пластинке 3, то его изображение примет положение 2′. Вместе с зеркалом 2 мысленно отобразим в полупрозрачной пластинке и все лучи, идущие справа от нее к зеркалу 2 и от него обратно к полупрозрачной пластинке. Тогда на экран P свет будет приходить, как бы отражаясь от двух плоскостей 1 и 2′. Если дополнить интерферометр двумя линзами, как это обычно делается (рис. 29), то, в зависимости от расстояния между линзой L 2 и экраном P, можно наблюдать полосы равной толщины (1/a 1 + 1/a 2 = 1/f 2 ) или полосы равного наклона (a 2 = f 2 ).
Дифракция — это огибание светом препятствий. Например, в опыте Юнга свет за каждой щелью распространяется не только в том направлении, в котором он распространялся до щели.
Возможность дифракции связана с тем, что свет за каждой щелью распространяется так, как если бы в плоскости щели находилась совокупность вторичных точечных источников света (принцип Гюйгенса). Правда, эти вторичные источники охотнее излучают в направлении, в котором свет распространялся до щели, чем в другие направления.
В произвольную точку за щелью свет от разных вторичных источников приходит в разных фазах. В каких–то направлениях при сложении этих волн в результате интерференции получаются колебания поля E с большой амплитудой, а в каких–то с малой амплитудой. В соответствии с этим говорят, что свет при дифракции на щели в одних направлениях распространяется, а в других — нет.










