Что можно сказать о взаимном расположении двух плоскостей которые имеют
Вариант 2.
1.Что можно сказать о взаимном расположении двух плоскостей, которые имеют три общие точки, не лежащие на одной прямой?
а) Пересекаются; б) ничего сказать нельзя; в) не пересекаются; г) совпадают; д) имеют три общие точки.
2. Какое из следующих утверждений верно?
а) Если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; б) прямая, лежащая в плоскости треугольника, пересекает две его стороны; в) любые две плоскости имеют только одну общую точку; г) через две точки проходит плоскость и притом только одна; д) прямая лежит в плоскости данного треугольника, если она пересекает две прямые, содержащие стороны треугольника.
3. Могут ли две различные плоскости иметь только две общие точки?
а) Никогда; б) могу, но при дополнительных условиях; в) всегда имеют; г) нельзя ответить на вопрос; д) другой ответ.
4. Точки K, L, M лежат на одной прямой, точка N не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось?
а) 1; б) 2; в) 3; г) 4; д) бесконечно много.
5. Выберите верное утверждение.
а) Через любые три точки проходит плоскость, и притом только одна; б) если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости; в) если две плоскости имеют общую точку, то они не пересекаются; г) через прямую и точку, лежащую на ней, проходит плоскость, и притом только одна; д) через две пересекающиеся прямые плоскость провести нельзя.
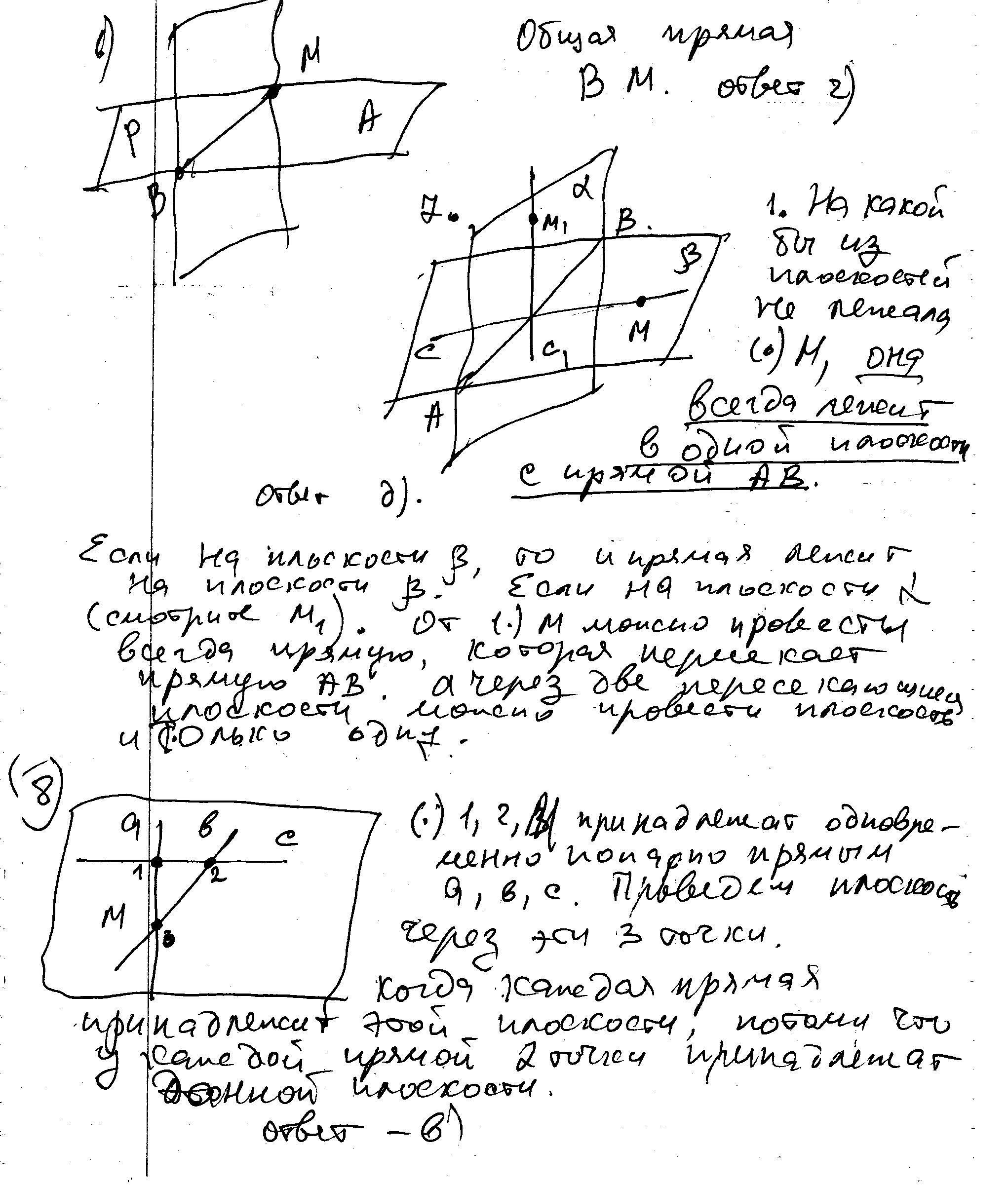
6. Назовите общую прямую плоскостей PBM и MAB.
а) PM; б) AB; в) PB; г) BM; д) определить нельзя.
7. Какую из перечисленных плоскостей пересекает прямая РМ (рис.1)?
а) DD1C; б) D1PM; в) B1PM; г) ABC; д) CDA.
В1 С1
8.Две плоскости пересекаются по прямой с. Точка М лежит только в одной из плоскостей. Что можно сказать о взаимном положении точки М и прямой с?
а) Никакого вывода сделать нельзя; б) прямая с проходит через точку М; в) точка М лежит на прямой с; г) прямая с не проходит через точку М; д) другой ответ.
9. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Что можно сказать о взаимном положении прямых а, b и c?
а) Все прямые лежат в разных плоскостях; б) прямые а и b лежат в одной плоскости; в) все прямые лежат в одной плоскости; г) ничего сказать нельзя; д) прямая с совпадает с одной из прямых: или с а, или с b.
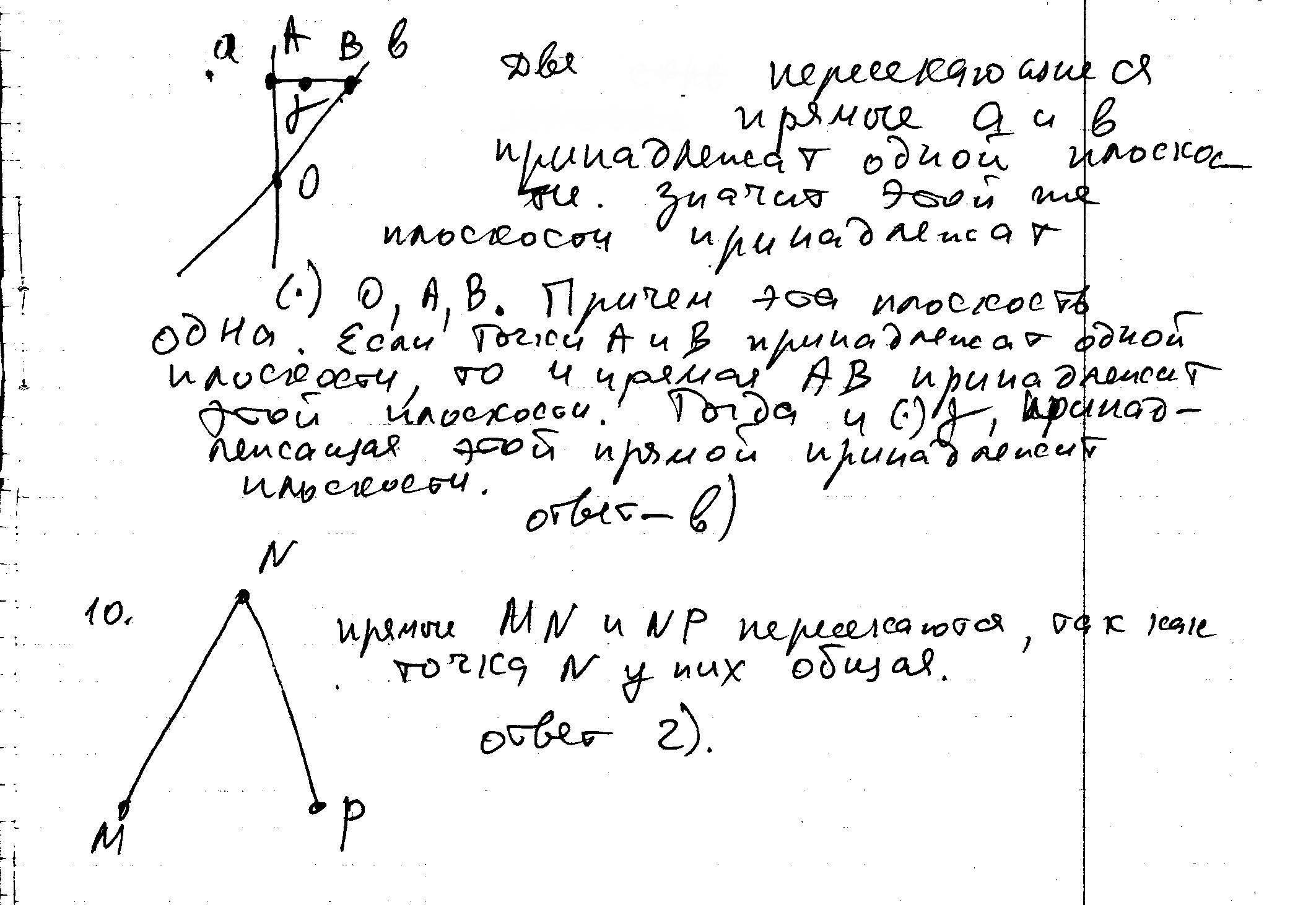
10. Прямые а и b пересекаются в точке О. A € a, B € b, Y € AB. Выберите верное утверждение.
а) Точки O и Y не лежат в одной плоскости; б) прямые OY и a параллельны; в) прямые a, b и точка Y лежат в одной плоскости; г) точки O и Y совпадают; д) точки Y и A совпадают.
1. Что можно сказать о взаимном расположении двух плоскостей, имеющих. Геометрия 10 класс Зив Б.Г. Математический диктант 1. Вариант 2
1. Что можно сказать о взаимном расположении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой?
1.
Что можно сказать о взаимном положении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой?
Решение: Совпадают.
3*. В указанной выше пирамиде найдите угол между гранями ВМС и DMC.
Опишите, пользуясь планом характеристики, химические элементы с атомными номерами 16 и 20.
Choose and read loud as quickly as you can the words on the topics “The Place We Live in” and “Furniture». Then see who is the ( Подробнее. )
1. Что можно сказать о взаимном расположении двух плоскостей, которые имеют три общие точки, не лежащие на одной прямой?
1. Что можно сказать о взаимном расположении двух плоскостей, которые имеют три общие точки, не лежащие на одной прямой?
А) Пересекаются ; б) ничего сказать нельзя ; в) не пересекаются ; г) совпадают ; д) имеют три общие точки.
2. Какое из следующих утверждений верно?
А) Если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости ; б) прямая, лежащая в плоскости треугольника, пересекает две его стороны ; в) любые две плоскости имеют только одну общую точку ; г) через две точки проходит плоскость и притом только одна ; д) прямая лежит в плоскости данного треугольника, если она пересекает две прямые, содержащие стороны треугольника.
3. Могут ли две различные плоскости иметь только две общие точки?
А) Никогда ; б) могут, но при дополнительных условиях ;
в) всегда имеют ; г) нельзя ответить на вопрос ; д) другой ответ.
4. Точки K, L, M лежат на одной прямой, точка N не лежит на ней.
Через каждые три точки проведена одна плоскость.
Сколько различных плоскостей при этом получилось?
А) 1 ; б) 2 ; в) 3 ; г) 4 ; д) бесконечно много.
5. Выберите верное утверждение.
А) Через любые три точки проходит плоскость, и притом только одна ; б) если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости ; в) если две плоскости имеют общую точку, то они не пересекаются ; г) через прямую и точку, лежащую на ней, проходит плоскость, и притом только одна ; д) через две пересекающиеся прямые плоскость провести нельзя.
6. Назовите общую прямую плоскостей PBM и MAB.
PB ; г) BM ; д) определить нельзя.
7. Две плоскости пересекаются по прямой с.
Точка М лежит только в одной из плоскостей.
Что можно сказать о взаимном положении точки М и прямой с?
А) Никакого вывода сделать нельзя ; б) прямая с проходит через точку М ; в) точка М лежит на прямой с ; г) прямая с не проходит через точку М ; д) другой ответ.
8. Прямые а и b пересекаются в точке М.
Прямая с, не проходящая через точку М, пересекает прямые а и b.
Что можно сказать о взаимном положении прямых а, b и c?
А) Все прямые лежат в разных плоскостях ; б) прямые а и b лежат в одной плоскости ; в) все прямые лежат в одной плоскости ; г) ничего сказать нельзя ;
д) прямая с совпадает с одной из прямых : или с а, или с b.
9. Прямые а и b пересекаются в точке О.
Выберите верное утверждение.
А) Точки O и Y не лежат в одной плоскости ; б) прямые OY и a параллельны ;
в) прямые a, b и точка Y лежат в одной плоскости ; г) точки O и Y совпадают ; д) точки Y и A совпадают.
10. Выясните взаимное расположение прямых MN и NP.
А) Параллельны ; б) скрещиваются ; в) определить нельзя ; г) пересекаются ; д) совпадают в любом случае.
Здесь все о взаимном расположении плоскостей, прямых и точек.
1а Через любые четыре точки, не лежащие на одной прямой, проходит плоскость и притом только однаДаНет2а Если три точки, принадлежащие прямой, лежат в плоскости, то все точки прямой лежат в этой плоско?
1а Через любые четыре точки, не лежащие на одной прямой, проходит плоскость и притом только однаДаНет2а Если три точки, принадлежащие прямой, лежат в плоскости, то все точки прямой лежат в этой плоскостиДаНет3а Через прямую и две точки, одна из которых лежит на прямой, а другая не лежит, проходит плоскость и притом только однаНетДа6в Если прямые EF и KL не лежат в одной плоскости, то прямые EK и LE не лежат в одной плоскостиДаНет7в Если две из четырех точек лежат на одной прямой, а две другие на прямой, пересекающей первую прямую, то все четыре точки лежат в одной плоскостиДаНет8в Если две хорды окружности лежат в плоскости, то и вся окружность лежит в этой плоскостиДаНет9в Через любые три точки круга, проходит плоскость и притом только однаДаНет10с Любая прямая, проходящая через точку пересечения медиан треугольника, имеет хотя бы одну общую точку с его сторонойДаНет11с Если два катета прямоугольного треугольника лежат в одной плоскости, то и весь треугольник лежит в этой плоскостиДаНет12с Если средняя линия трапеции лежит в плоскости, то и вся трапеция лежит в этой плоскостиДаНет.
1. Какое из следующих утверждений верно?
1. Какое из следующих утверждений верно?
А) любые четыре точки лежат в одной плоскости ; б) любые три точки не лежат в одной плоскости ; в) любые четыре точки не лежат в одной плоскости ; г) через любые три точки проходит плоскость ; д) через любые три точки проходит плоскость, и притом только одна.
2. Сколько общих точек могут иметь две различные плоскости?
А) 2 ; б) 3 ; в) несколько ; г) бесконечно много ; д) бесконечно много или ни одной.
3. Точки А, В, С лежат на одной прямой, точка D не лежит на ней.
Через каждые три точки проведена одна плоскость.
Сколько различных плоскостей при этом получилось?
А) 2 ; б) 3 ; в) 1 ; г) 4 ; д) бесконечно много.
4. Если три точки не лежат на одной прямой, то положение плоскости в пространстве они : а) не определяют в любом случае ; б) определяют, но при дополнительных условиях ; в) определяют в любом случае ; г) ничего сказать нельзя ; д) другой ответ.
5. Выберите верное утверждение.
6. Назовите общую прямую плоскостей AFD и DEF.
А) AD ; б) DE ; в) определить нельзя ; г) DF ; д) AF.
7. Какую из перечисленных плоскостей пересекает прямая EF (рис.
1)? а)ABC ; б) AA1D ; в) BB1C1 ; г) AEF ; д) B1C1C.
Рис. 1 B1 C1 A1 D1 E F В С А D 8.
Через точку М, не лежащую на прямой а, провели прямые, пересекающие прямую а.
9. Прямая а лежит в плоскости α и пересекает плоскость β.
Каково взаимное расположение плоскостей α и β?
А) Определить нельзя ; б) они совпадают ; в) имеют только одну общую точку ; г) не пересекаются ; д) пересекаются понекоторой прямой.
10. Точки A, B, C не лежат на одной прямой.
M € AB ; K € AC ; X € MK.
Выберите верное утверждение.
А) X € AB ; б) X € AC ; в) X € ABC ; г) точки Х и М совпадают ; д) точки Х и К совпадают.
Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости?
Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости.
В каком случае 3 точки в пространстве не определяют положение плоскости, проходящей через эти точки?
В каком случае 3 точки в пространстве не определяют положение плоскости, проходящей через эти точки?
Могут ли 2 различные плоскости иметь только одну общую точку?
Точка М не лежит на прямой а.
Лежат ли эти прямые в одной плоскости?
Помогите даны две различные прямые, пересекающиеся в точке А?
Помогите даны две различные прямые, пересекающиеся в точке А.
Докажите, что все прямые, пересекающие обе данные прямые и не проходящие через точку А, лежат в одной плоскости.
Какое из следующих утверждений верно?
Какое из следующих утверждений верно?
А) Если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости ; б) прямая, лежащая в плоскости треугольника, пересекает две его стороны ; в) любые две плоскости имеют только одну общую точку ; г) через две точки проходит плоскость и притом только одна ; д) прямая лежит в плоскости данного треугольника, если она пересекает две прямые, содержащие стороны треугольника.
Помогите пожалуйста34?
A) Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
B) В любом треугольнике каждая сторона больше суммы двух других сторон.
C) Если две различные прямые имеют общую точку, то через них можно провести множество плоскостей.
D) Через четыре точки не лежащие на одной прямой можно провести плоскость и притом только одну.
Прямые в пространстве параллельны если они лежат в одной плоскости и имеют две общие точки
b) Через точку пространства можно провести прямую параллельную данной и при том только одну.
C) Если две параллельные прямые пересекают третью, то все они параллельны
d) Если две прямые не пересекаются и не лежат в одной плоскости, то они скрещивающиеся.
Прямая и плоскость называются параллельными, если они имеют две общие точки.
C) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей не параллельна данной прямой.
D) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая пересекает эту плоскость.
B) Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны
c) Отрезки параллельных прямых заключенных между параллельными плоскостями пересекаются.
D) Две плоскости называются параллельными если они имеют общие точки.
38. Если одна из двух параллельных прямых перпендикулярна к третьей, то другая прямая
Перпендикулярна этой прямой
b) Параллельна этой прямой
Скрещивается с этой прямой
d) Не возможно определить.
39. Если две прямые перпендикулярны к плоскости, то они между собой :
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости
Пересекаются под острым углом
Расстояние между параллельными плоскостями в пространстве измеряют по
b) По проекции наклонной
d) Неважно как измерять.
Докажите что любые прямые пересекающие эти прямые и не проходящие через точку М, лежат в одной плоскости.
Прямые а в с имеют общую точку верноли что данные прямые лежат в одной плоскости ответ обьясните?
Прямые а в с имеют общую точку верноли что данные прямые лежат в одной плоскости ответ обьясните.
Плоскости альфа и бета пересекаются по прямой с.
Прямая а лежит в плоскости альфа и пересекается в плоскости бета.
Какоовзамное расположение прямых а и с ответ обьясните.
Взаимное расположение двух плоскостей.
Две различные плоскости в пространстве либо параллельны, либо пересекаются.
Параллельность двух плоскостей
Определение. Две плоскости в пространстве называются параллельными, если они не пересекаются.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.
Основные свойства параллельности плоскостей.
Пересечение двух плоскостей
Две плоскости пересекаются по прямой. Общая прямая двух плоскостей называется ребром двугранного угла, образованного при пересечении данных плоскостей. При пересечении двух плоскостей образуются четыре двугранных угла. Если все они равны, то плоскости называются перпендикулярными.
Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Из признака перпендикулярности плоскостей следует, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Угол между плоскостями — наименьший из двугранных углов, образованных при пересечении плоскостей.
Угловая величина двугранного угла — это величина линейного угла данного двугранного угла.
Чтобы найти линейный угол двугранного угла надо из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру. Все линейные углы двугранного угла равны друг другу.
Тренировочные задания
Дан куб 
. Найдите угол между плоскостями 
и 
.
Дан куб . Точка 
— середина ребра 
. Найдите угол между плоскостями 
и 
.
В кубе все рёбра равны 
. На его ребре 
отмечена точка так, что 
. Через точки и 
построена плоскость 
, параллельная прямой 
. Найдите угол наклона плоскости к плоскости грани 
.
Дана правильная треугольная призма 
, у которой сторона основания равна 
, а боковое ребро равно 
. Через точки 
, и середину 
ребра 
проведена плоскость. Найдите угол между плоскостью сечения и плоскостью ABC.
Все рёбра правильной треугольной призмы имеют длину 
. Точки 
и 
— середины рёбер 
и 
соответственно. Найдите угол между плоскостями 
и 
.
Основанием пирамиды 
является прямоугольник 
, в котором 
. Диагонали прямоугольника пересекаются в точке 
. Отрезок 
является высотой пирамиды . Из вершин 
и 
опущены перпендикуляры 
и 
на ребро 
. Найдите двугранный угол пирамиды при ребре , если 
.
В основании прямой призмы лежит квадрат со стороной 
, а высота призмы равна 
. Точка 
лежит на диагонали , причём 
. Найдите угол между плоскостью 
и плоскостью 
.