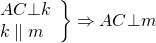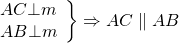Что можно сказать о четырехугольнике если серединные перпендикуляры пересекаются в одной точке
Серединные перпендикуляры к сторонам треугольника
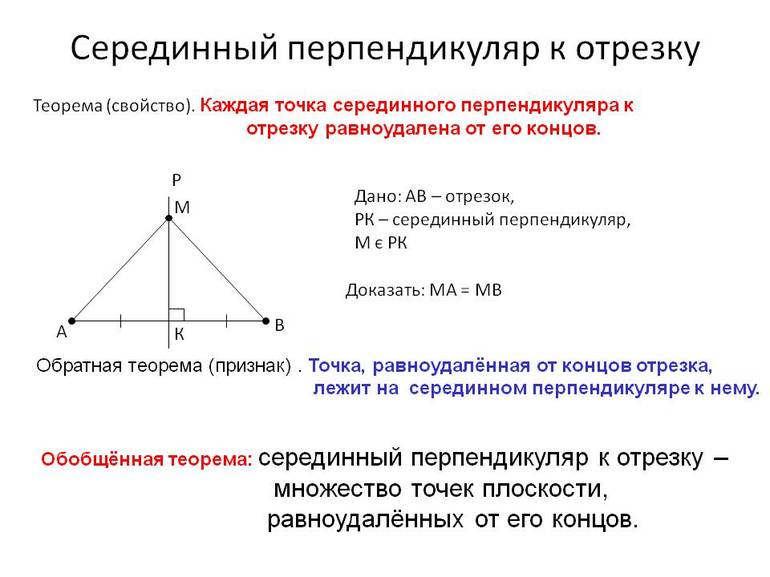
Свойство серединных перпендикуляров к сторонам треугольника
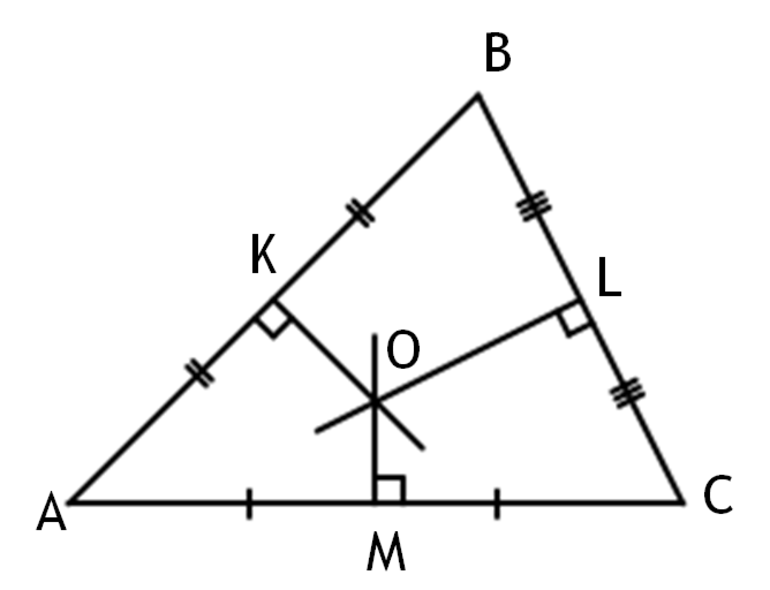
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
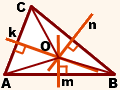
m, n, k — серединные перпендикуляры к сторонам AB, BC, AC
Доказать: m, n, k пересекаются в одной точке.
Сначала докажем, что серединные перпендикуляры к двум сторонам треугольника пересекаются в одной точке.
Предположим, что m и k не пересекаются. Тогда m ∥ k.
Но прямые AB и AC пересекаются в точке A. Пришли к противоречию. Следовательно, прямые m и k пересекаются.
Обозначим точку пересечения прямых m и k как O.
По свойству серединного перпендикуляра к отрезку AO=OC и AO=BO. Следовательно, и OC=BO. Значит, точка O равноудалена от концов отрезка BC, следовательно, лежит на серединном перпендикуляре n к этому отрезку. Таким образом, все три серединных перпендикуляра m, n, k к сторонам треугольника ABC пересекаются в одной точке O.
Что и требовалось доказать.
Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной около этого треугольника окружности
Точка пересечения серединных перпендикуляров к сторонам треугольника — одна из четырех замечательных точек треугольника.
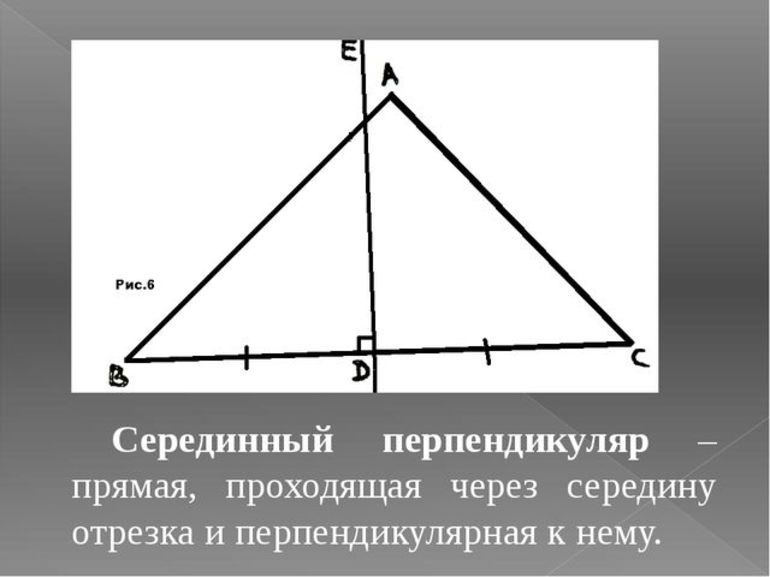
Серединный перпендикуляр
Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?
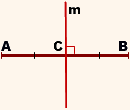
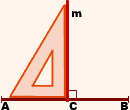
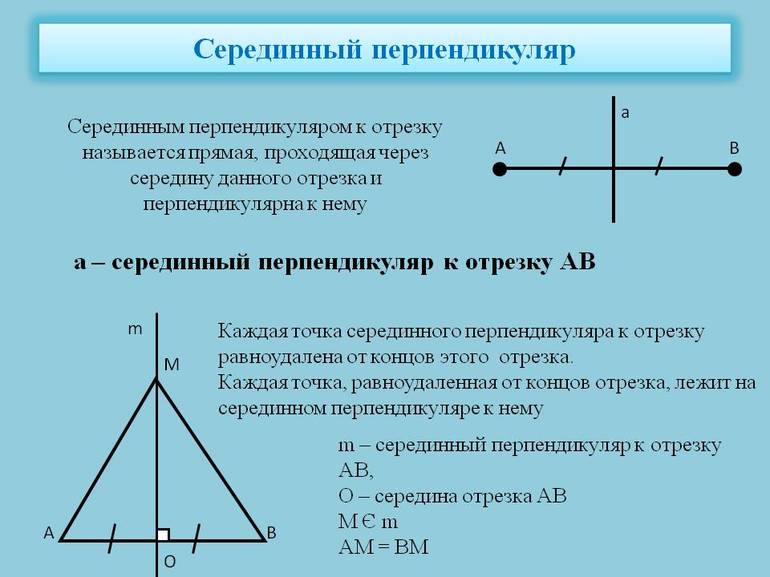
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
m — серединный перпендикуляр к отрезку AB, если
точка C — середина отрезка AB,
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:
1) найти середину отрезка;
2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):
Свойства серединного перпендикуляра.
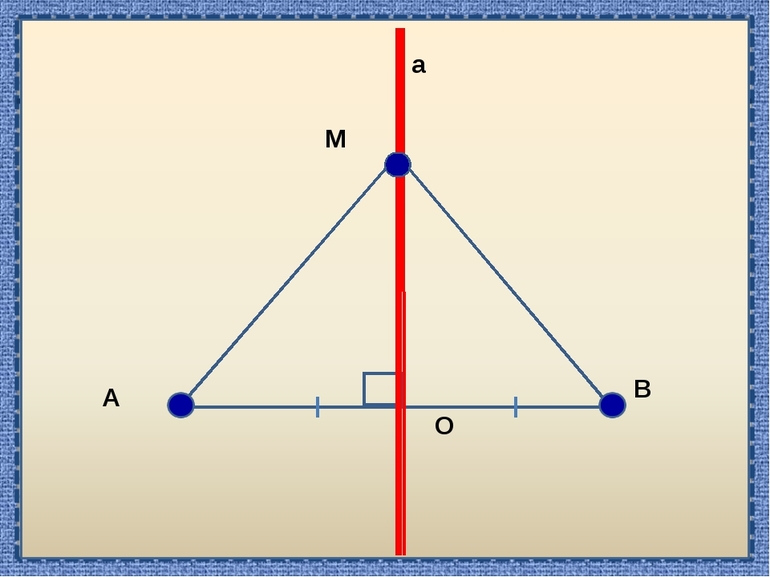
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
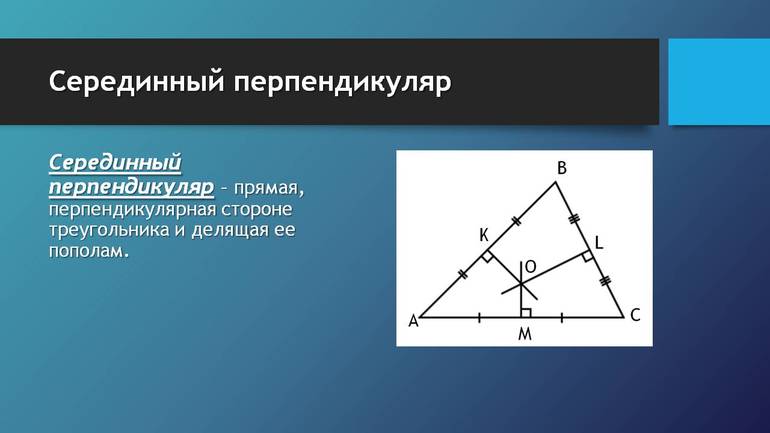
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Общие сведения
Серединным перпендикуляром отрезка называют прямую, которая проходит под прямым углом через среднюю точку, т. е. середину отрезка. Для полного понимания материала следует остановиться на базовых элементах геометрии.
Точка — единица, при помощи которой строятся прямые, отрезки, лучи и фигуры. Прямая — простая фигура в форме бесконечной линии, состоящей из множества точек, лежащих в одной плоскости. Луч — базовая геометрическая фигура в виде бесконечной линии с одной стороны и точки-ограничителя — с другой. Иными словами, луч имеет начало, но не имеет конца. Отрезок — некоторая часть прямой (луча или другого отрезка), ограниченная двумя точками.
Кроме того, в геометрии серединный перпендикуляр встречается в треугольниках. Из определения можно сделать вывод, что им может быть прямая, отрезок и даже луч.
Аксиомы геометрии Евклида
Евклидовой геометрией называется наука о фигурах на плоскости, основанная на аксиомах и теоремах. Аксиома — базовое утверждение, не требующее доказательства. Оно используется для доказательства каких-либо теорем. Математики выделяют пять аксиом:
Формулировка первой имеет такой вид: если существует в геометрическом пространстве плоскость, состоящая из множества точек, то через любые из них можно провести только одну прямую. Иными словами, можно взять произвольные две точки и провести через них одну прямую. Чтобы начертить еще одну прямую, следует взять две другие точки.
Следующее утверждение называется аксиомой порядка. Она гласит, что существует точка, которая лежит между двумя другими на прямой. Значение слова «конгруэнтность» не совсем понятно для новичка, однако нужно постепенно привыкать к терминологии. Оно обозначает «равенство». Третий геометрический факт формулируется таким образом: когда два отрезка или угла конгруэнтны третьему, тогда они равны между собой. Аксиома касается только отрезков и углов.
Чтобы убедиться в ее правильности, нужно разобрать следующий пример: длина первого отрезка составляет 10 см, второго — тоже, а третий равен первому. Необходимо доказать, что они равны между собой. Это делается очень просто:
Следует отметить, что данные действия оказались лишними — было потрачено время на понимание простой «истины». Параллельность прямых является также аксиомой и формулируется таким образом: если существует некоторая прямая на плоскости и точка, не лежащая на ней, то через последнюю можно провести только одну параллельную ей прямую.
И последняя аксиома называется Архимедовой. Ее формулировка имеет такой вид: для произвольных отрезков, лежащих на одной прямой, существует некоторая последовательность базовых элементов (точек), лежащих на одном и другом отрезках, таких, что заданные их части равны между собой. Иными словами, на одной прямой могут быть расположены равные между собой отрезки.
Информация о треугольниках
Треугольником является любая фигура, состоящая из трех вершин (точек) соединенных отрезками (сторонами), причем точки не лежат на одной прямой в одной плоскости. Они классифицируются по такому типу:
В первом случае фигуры делятся на остроугольные, тупоугольные и прямоугольные. Остроугольным называется треугольник, у которого все углы острые (меньше 90 градусов). У тупоугольного — один угол тупой (> 90), а в прямоугольном — один из углов равен 90 градусам. Следует отметить, что сумма градусных мер углов любого треугольника эквивалентна 180.
Когда стороны у треугольника неравны между собой, тогда его называют разносторонним. При равенстве двух боковых сторон он считается равнобедренным, у которого третья сторона — основание. Если все стороны равны, то значит, фигура является равносторонней или правильной.
У треугольника есть еще и другие параметры. Их называют медианой, биссектрисой и высотой. Первый параметр является отрезком, который проводится из любой вершины на среднюю точку стороны. Высота — часть прямой, которая проводится из произвольной вершины и перпендикулярна противоположной стороне. Биссектрисой называется прямая, делящая угол на две равные части.
Медиана, высота и биссектриса, проведенные из вершины к основанию, совпадают и эквивалентны серединному перпендикуляру в треугольниках равнобедренного и равностороннего типов. Это очень важно при решении задач. Еще одним признаком, по которому выполняется классификация — подобность треугольников. У них могут быть равными только углы и некоторые стороны. Они отличаются между собой по определенному параметру, который называется коэффициентом подобия. Последний влияет только на размерность сторон. Говорят, что фигуры подобны по определенному признаку (их всего три).
Основные теоремы
Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.
Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:
Первая теорема называется прямой о СП. Она показывает, каким свойством обладают точки серединного перпендикуляра. Ее формулировка следующая: произвольная точка, которая взятая на перпендикуляре, удалена на равные расстояния от конечных точек отрезка, ограничивающих его на плоскости.
Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.
Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.
Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.
Важные свойства
Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:
В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.
Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:
Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:
В основном по таким соотношениям и нужно определить площадь. Полупериметр вычисляется таким образом: р = (а + b + с) / 2.
Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.
Пример решения задачи
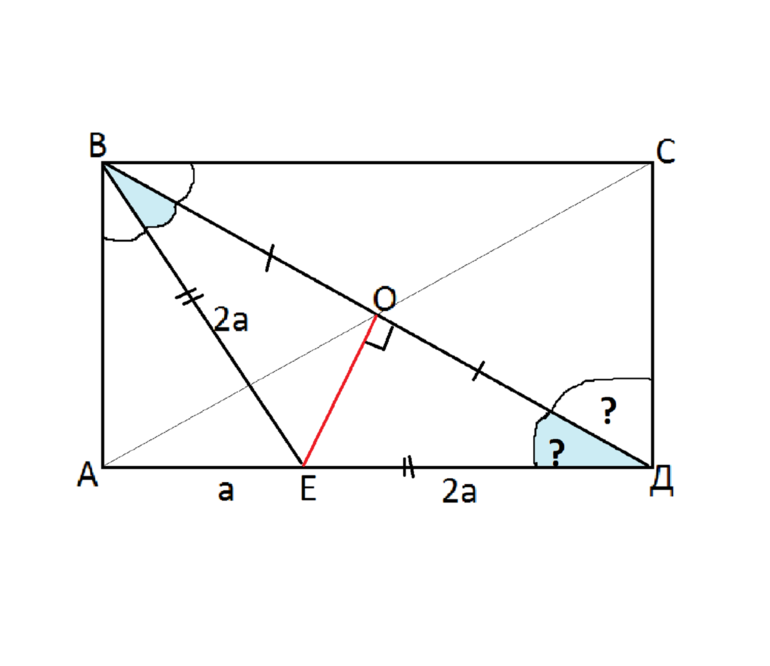
В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:
Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении
Рисунок 1. Чертеж для решения задачи.
Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:
Таким образом, нахождение серединного перпендикуляра позволяет значительно уменьшить объемы вычислений. Однако для этого нужно знать не только основные теоремы, но и его свойства.
Цикличный четырехугольник, работа учащейся 9 класса Ригонен Анастасии, представленная на сессию МАН, занявшая первое место
Министерство образования и науки, молодежи и спорта
Автономной Республики Крым
МАЛАЯ АКАДЕМИЯ НАУК ШКОЛЬНИКОВ КРЫМА «ИСКАТЕЛЬ»
Условия цикличности четырех точек
Работу выполнила: Ригонен Анастасия
(Симферопольский район, МБОУ
«Гвардейская школа-гимназия №2», 9 кл.)
Научный руководитель: Исаева Н. Н.,
учитель высшей категории
МБОУ «Гвардейской школы-гимназии №2»
Ригонен Анастасия Дмитриевна
Ученица 9-Б класса МБОУ «Гвардейская школа-гимназия №2»
Исаева Нина Николаевна, руководитель,
Учитель математики МБОУ «Гвардейская школа-гимназия №2»
Тема:Условия цикличности четырех точек
Цель: Выяснение практических областей применения четырех точек на окружности
Задачи: изучение информации о цикличных четырехугольниках в интернете, школьных пособиях и учебниках. Систематизация полученной информации и формулировка выводов по теме исследования.
Актуальность данного исследования связана с необходимостью обобщению теоретического материала по изучаемой теме, его практической ценностью для решения большого количества задач как базовой программы, так и повышенной сложности.
Предмет исследования : Четыре точки, лежащие на одной окружности
Мой личный вклад в работу заключается в исследовании школьной литературы и разных источников с целью обобщения и систематизации свойств цикличности, методов применения к решению задач.
Практическое значение работы : материал данной исследовательской работы можно в дальнейшем будет использовать на уроках геометрии, при подготовке к ГИА и олимпиадам.
Выводы: изучение представленного материала позволяет более детально изучить проблему, рассмотреть аналогию ее и определить место в логическом изложении школьной программы.
Окружность и четырехугольники
2.1 Вписанные четырехугольники………………………………………………9
2.2 Первое условие цикличности………………………………………………..9
2.2 Второе условие цикличности……………………………………………….10
2.3 Третье условие цикличности………………………………………………..11
2.4 Четвертое условие цикличности……………………………………………11
2.5 Пятое условие цикличности………………………………………………. 12
Применение условий на практике
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………………………..19
Темой представленной исследовательской работы является цикличный четырехугольник.
Целью данной работы было выяснение практического применения цикличного четырехугольника в решении задач.
Объектом исследования являются свойства четырех точек, лежащих на одной окружности.
В качестве методов исследования в работе были использованы:
Систематизация теоретического материала.
Анализ и синтез изучаемого материала.
Аналитический метод исследования.
Достижение поставленной цели осуществлялось через решение некоторых задач, таких как:
Сбор теоретического материала по теме и его систематизация
Изучение возможности практического применения теоретической база
Применение условий цикличного четырехугольника в задачах по геометрии
Оформление проработанной информации в виде проекта.
Актуальность изучаемой темы обусловлена возможностью применения условия цикличности для решения задач, так как установление факта описания окружности около четырехугольника часто является ключом к решению задачи.
Формы круга, окружности мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Математики стали изучать окружность и круг на плоскости очень давно.
Сотни лет астрономы считали, что планеты двигаются по окружностям.
Круглые тела тоже в древности заинтересовали человека. Так в Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Позже вместо бревен стали использовать их части – в виде колес, которые катились уже легче.
В Древней Греции, где все разрозненные знания привели в систему, “окружность” и “круг” получили свои названия. Там же многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны.
Современные определения круга и окружности следующие.
Окружность- это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Круг — это геометрическая фигура, которая ограничена окружностью.
Математиками были рассчитаны формулы, позволяющие определить ряд показателей круга и окружности.
Со школьных времен всем знакомы эти две формулы:
Формула площади круга
И формула длины окружности
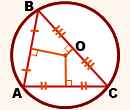
Как известно, около любого треугольника можно описать окружность. Теорем, доказывающих данное положение несколько. Одно из доказательств представлено ниже.
По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):
Так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, то точка A — центр описанной около треугольника CED окружности. Что и требовалось доказать.
По теореме, центр окружности будет находится на пересечении серединных перпендикуляров (ортоцентр). Эта точка может находиться как и в треугольнике, так и за его пределами.
Центр описанной окружности около остроугольного треугольника лежит внутри треугольника. У тупоугольного треугольника ортоцентр лежит вне его. У прямоугольного треугольника же центр описанной окружности лежит на середине гипотенузы. Замечу, что у правильного треугольника центр описанной и вписанной окружности совпадает.
Практическая значимость представленных свойств описанной окружности велика, так как можно вывести ряд формул, позволяющих рассчитать величины сторон треугольника по величинам элементов описанной вокруг него окружности.
Например, представим вычисление радиусов описанных окружностей для различных видов треугольников:
Произвольных треугольников (Применяя формулу Герона)
Произвольных треугольников (Применяя теорему синусов)
Равнобедренных треугольников (Применяя формулу Герона)
Прямоугольных треугольников (применяя теорему Пифагора)
В целом, всякий треугольник имеет одну описанную окружность, одну вписанную и три вневписанных. Но уже не всякий четырехугольник имеет вписанную и описанную окружность.
Окружность и четырехугольники
Итак, окружность можно описать вокруг любого треугольника, но не любого четырехугольника. Для того, чтобы четырехугольник мог быть вписан в окружность, необходимо и достаточно выполнение условий.
Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника. В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.
Четырехугольник же иногда называют cyclic quadrilateral, что в переводе означает «циклический четырехугольник».
Если в сложной геометрической задаче удается установить, что какие-то четыре точки лежат на одной окружности, то это зачастую оказывается существенным продвижением к решению. Поэтому нужно свободно владеть свойствами и признаками расположения четырех точек на окружности.
Первое условие цикличности
Если суммы противоположных сторон равны, то четыре точки лежат на одной окружности.
Из этого следует, что окружность около ромба можно описать только тогда, когда он является квадратом, а описание окружности около стандартного, так сказать, ромба, который мы привыкли видеть, и вовсе невозможно (2 условие цикличности).
Второе условие цикличности
Если сумма противоположных углов равна 180 градусов, то четыре точки лежат на одной окружности.
Это и есть самое главное условие. Его можно легко доказать.
Докажем теорему методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A, B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга.
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E, и соединим отрезком точку E с точкой A. Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180°. При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы. Отсюда вытекает, что угол ADC равен углу AEC. Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC, не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Из этого следует, что окружность можно описать около трапеции только если она равнобедренная.
У дельтоида же можно описать окружность только тогда, когда он состоит из двух одинаковых равнобедренных треугольников.
Параллелограмм имеет описанную окружность тогда, когда он прямоугольник.
Третье условие цикличности
Описать окружность можно около любого четырехугольника, у которого пересекаются в одной точке четыре серединных перпендикуляра.
Это условие следует из того, что центром описанной около четырехугольника окружности является точка пересечения серединных перпендикуляров.
Четвертое условие цикличности
Если произведение диагоналей четырёхугольника равно сумме произведений противоположных сторон, то четыре точки цикличны.
Данная теорема установлена Клавдием Птолемеем во втором веке нашей эры. Доказать, в свою очередь, ее очень легко. Я выбрала несколько доказательств, которые понравились мне. Первое доказательство будет в основном следовать доказательству самого Птолемея, приведенному им в книге «Альмагест». Используется подобие треугольников.
В то же время ABD = MBC (т. к. ABM = DBC), а BCA = BDA, как опирающиеся на одну хорду AB. Значит, AD/BD = MC/BC, или, перемножая крест на крест, MC ∙ BD = AD ∙ BC.
Складывая почленно равенства MA ∙ BD = AB ∙ CD и
MC ∙ BD = AD ∙ BC, получаем (MA + MC) ∙ BD = AB ∙ CD + AD ∙ BC, или AC ∙ BD = AB ∙ CD + BC ∙ AD, что и требовалось доказать.
2. Пусть ABC’ — произвольный треугольник. Проведём через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углуABD. Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Что и требовалось доказать.
Пятое условие цикличности
Называют ее второй теоремой Птолемея. Выглядит она так:
Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Применение условий на практике
В XVII веке в Японии возникла сильная математическая школа, связанная с многовековыми традициями китайской математики и не имевшая контактов с современной математикой Запада.
Метод открытия геометрических теорем, практиковавшийся японскими геометрами, основывался на интенсивной и продолжительной концентрации на рассматриваемом чертеже. Когда одного геометра спросили, как он получил свои замечательные теоремы об эллипсах, он ответил, что не размышлял ни над чем, кроме эллипсов, в течение последних десяти лет! Интересно, что когда японские геометры получили в свои руки китайский перевод «Начал» Евклида, они были очень сильно удивлены. «Зачем, — сказали они, — доказывать такие очевидные факты, когда есть ещё столько красивых и сложных геометрических теорем?»
Рассмотрим одну из таких типичных теорем.
Разбиение произвольного вписанного четырёхугольника диагоналями даёт четыре перекрывающих друг друга треугольника каждая диагональ создаёт два треугольника). Центры вписанных в эти треугольники окружностей образуют прямоугольник.
По результатам проделанной работе можно сделать ряд выводов:
-Окружность, как и треугольник, является одной из основных фигур геометрии, которые помогают в решении многих практических задач.
-Свойства окружности были открыты и описаны еще в древности.
-Не каждый четырехугольник можно вписать в окружность.
— Если в сложной геометрической задаче удается установить, что какие-то четыре точки лежат на одной окружности, то это зачастую оказывается существенным продвижением к решению.
— Изученные свойства описанных окружностей и свойства цикличности позволяют решать сложные геометрические задачи, то есть имеют широкий спектр методов практического использования.
Список использованной литературы:
Энциклопедический словарь юного математика/Сост. Э-68 А.П.Савин- М.: Педагогика, 1989.