Что можно считать первым инструментом для счета
От счетных палочек к арифмометру
Вначале люди учились считать, используя собственные пальцы. Затем в ход пошли мелкие предметы — камешки, ракушки, палочки и т.п. Когда же этого оказалось недостаточно, возникли простейшие счетные приспособления. Особое место среди них занял старинный вычислительный инструмент, получивший название «абак» от латинского слова «abacus» — «доска».
Считается, что впервые абак появился в Месопотамии около 3500 лет до н.э. Сделать его было совсем несложно — достаточно было разлинеить столбцами дощечку или просто нарисовать столбцы на песке. Каждому из столбцов присваивалось значение разряда чисел: единиц, десятков, сотен, тысяч. Числа обозначались набором камешков, раскладываемых по различным столбцам — разрядам. Добавляя или убирая из соответствующих столбцов то или иное количество камешков, можно было производить не только сложение или вычитание, но даже умножение и деление, многократно повторяя операцию сложения или вычитания соответственно.
Китайский суаньпань
В Древнем Китае для счета применяли инструмент, построенный по принципу абака — суаньпань. Он появился примерно в VI в. н.э. и представлял собой прямоугольную деревянную раму, в которой параллельно друг другу были протянуты проволоки или веревки. Они соответствовали десятичным разрядам. Обычно их число равнялось девяти, но для подсчета больших величин их могло быть и больше. По длине рамка суаньпань была разделена на две неравные части. В большом отделении, обозначавшем землю, на каждой проволоке было нанизано по пять шариков (косточек), в меньшем («небо») — по два.
Более совершенный соробан
Ориентировочно в XVI в. суаньпань из Китая попал в Японию. Здесь его несколько переделали и дали другое название — соробан. Японские счеты представляли собой прямоугольную раму, которая могла содержать несколько десятков вертикальных палочек. И чем больше их было, тем с большим числом разрядов цифр можно было проводить математические операции. На каждой палочке находилось по пять косточек, разделенных поперечной полосой — над полосой одна косточка, под полосой — четыре. Некоторые японцы настолько виртуозно владели соробаном, что по скорости счета могли поспорить даже с калькулятором.
Простой счетный прибор
По принципу действия очень похожи на абак традиционные русские счеты. Только роль столбцов в них выполняют горизонтальные направляющие из проволоки с нанизанными на них косточками. На Руси счеты были незаменимым инструментом торговцев, приказчиков, чиновников. Даже в конце прошлого века их активно использовали в магазинах для счета вместо калькулятора. А из России этот простой и полезный счетный прибор проник и в Европу.
Инструмент для сложных вычислений
К немеханическим счетным устройствам также относится логарифмическая линейка — инструмент для быстрого выполнения таких сложных математических операций, как умножение и деление, возведение в степень (чаще всего в квадрат и куб), вычисление логарифмов и тригонометрических функций. Считается, что первая логарифмическая линейка была изготовлена англичанином Робертом Биссакером (1620—?) в 1654 г. Она состояла из линейки с нанесенной на ней логарифмической шкалой и подвижного бегунка. Вычисления производились путем перемещения движка вдоль линейки, при этом результат отображался на ее шкале.
Современная логарифмическая линейка состоит из двух шкал в логарифмическом масштабе, способных передвигаться относительно друг друга. Более сложные ее варианты могут содержать дополнительные шкалы и прозрачный бегунок с несколькими рисками.
Простота арабских цифр
Мы привыкли к тому, что цифры 1,2, 3 и т.д., которыми мы пользуемся ежедневно, называются арабскими и придумали их арабы. На самом деле эти цифра возникли в Индии примерно в IV—V вв. Просто арабы принесли оттуда эту форму записи чисел, которая потом распространилась через Северную Африку, Испанию и в X в. попала в Европу.
Преимущество арабских цифр по сравнению с римскими не в их написании, а в гениальном изобретении, при котором «вес» цифры определяется ее положением. Так, например, 3 в числе 23 «весит» всего три единицы, а уже в числе 232 — три десятка единиц. Представьте, какие бы сложные вычисления нам пришлось производить, если бы до сих пор пользовались римскими числами. Чтобы понять это, попробуйте, например, перемножить XVII на СХХIII (17 на 123).
Считающие часы
Первый механический калькулятор, умевший выполнять различные арифметические действия, был построен немецким ученым Вильгельмом Шикардом (1592—1633) в 1623 г. Изобретатель назвал свою машину «Считающими часами». Вероятно, такое название она получила из-за того, что, как и в настоящих часах, работа ее механизма была основана на использовании звездочек и шестеренок.
«Считающие часы» Шикарда умели складывать и вычитать шестизначные числа и информировали пользователя о переполнении с помощью звонка. По некоторым данным, с помощью этого изобретения друг Шикарда, известный немецкий философ и астроном Иоганн Кеплер (1571—1630), рассчитывал сложнейшие астрономические таблицы.
К сожалению, сама машина и ее чертежи были потеряны в годы Второй мировой войны. Однако в 1960 г. группа энтузиастов построила точную копию этого вычислителя по обнаруженным древним записям и подтвердила его существование и работоспособность.
Счетная машина Паскаля
Более совершенное механическое счетное устройство удалось построить в 1642 г. выдающемуся французскому ученому Блезу Паскалю (1623—1662). Механический «компьютер», названный ученым «Паскалина», мог складывать и вычитать любые числа до одного миллиона.
Машина Паскаля представляла собой механическое устройство в виде деревянного ящика с многочисленными связанными одна с другой шестеренками и набором вертикально установленных колес с нанесенными на них цифрами от 0 до 9. Складываемые числа вводились в машину при помощи соответствующего поворота наборных колесиков. При полном обороте колесо сцеплялось с соседним и поворачивало его на одно деление. Ответ появлялся в верхней части металлического корпуса.
Примерно за 10 лет Паскаль построил около 50 экземпляров своей машины. Сложность и высокая стоимость «Паскалины» в сочетании с небольшими вычислительными способностями послужили препятствием ее широкому распространению. Но зато заложенный в основу машины Паскаля принцип связанных колес в дальнейшем использовался в большинстве создаваемых вычислительных устройств.
Устройство для умножения и деления
В 1673 г. немецкий математик и философ Готфрид Вильгельм Лейбниц (1646—1716) создал механическое счетное устройство, которое не только складывало и вычитало, но умножало и делило 12-разрядные числа. В основе механизма лежал изобретенный Лейбницем ступенчатый валик, представлявший собой цилиндр с нанесенными на нем зубцами различной длины. Ускорить повторяющиеся операции сложения позволяла специальная рукоятка, с помощью которой пользователь вращал цилиндр.
По некоторым данным один экземпляр счетной машины Лейбница был приобретен Петром I, который затем подарил его китайскому императору, желая удивить последнего европейскими техническими достижениями. Кстати, именно зубчатые колеса Лейбница в дальнейшем стали основой массовых счетных приборов — арифмометров, которыми широко пользовались вплоть до середины XX в.
Коммерческий успех и долгая жизнь
Производство счетных машин длительное время оставалось делом невыгодным. Лишь в 1820 г. французскому предпринимателю Шарлю-Ксавье Тома де Колмару (1785—1870) удалось создать первый механический счетный прибор, принесший своему изобретателю коммерческий успех.
В своей машине Колмар использовал принцип построения счетного механизма Лейбница, что позволяло быстро производить основные математические операции. Получив патент на свою машину, изобретатель запустил ее в массовое производство. Достаточно быстро она завоевала звание самой надежной счетной машины и не случайно занимала достойное место на столах счетоводов Европы. Кроме того, этот вычислитель поставил своеобразный мировой рекорд по продолжительности продаж: последняя модель была продана в начале XX в.
Прообраз компьютера
В середине XIX в. английский математик Чарльз Бэббидж (1792—1871) разработал «аналитическую машину», которая по своей конструкции напоминала современный компьютер. Она могла оперировать с 40-разрядными числами, а ее вычислительное устройство (процессор) имело два блока для хранения промежуточных результатов. Кроме того, в машину был встроен своеобразный банк данных (память), в котором могли храниться несколько десятков чисел. Информация (данные) и порядок выполнения операций (программа) в «аналитическую машину» Бэббиджа вводились с перфокарт, а результаты выводились на печатающее устройство (принтер).
По свидетельству очевидцев, такая машина складывала числа за 3 секунды, а операции умножения и деления занимали до 4 минут.
Популярность арифмометра
В первой половине XX в. большим спросом у работников, занимавшихся расчетами, пользовались настольные механические счетные устройства, действующие на основе сложения. Они назывались «арифмометры» — от греческого слова «число» — и выполняли операции сложения, вычитания, умножения и деления. Механизм арифмометра приводился в действие рычагом. Так, например, для сложения надо было выставить на рычажках первое слагаемое. Затем повернуть ручку арифмометра, при этом число на рычажках вводилось в счетчик суммирования. После этого на рычажках устанавливалось второе слагаемое, и ручка вновь поворачивалась. При этом число на рычажках прибавлялось к числу, находящемуся в счетчике суммирования, и на счетчике появлялся результат сложения.
В течение многих десятков лет арифмометр был самой распространенной вычислительной машиной. И только появление компактных электронных калькуляторов вытеснило его из всеобщего употребления.
Развитие счётных машин
с древних времён
до наших дней
Можно подумать, будто счётная машина — это современное явление. Однако человечество стало изобретать устройства для счёта задолго до того, как появились первые компьютеры.
Самыми первыми человеческими помощниками в счёте были пальцы. С их помощью наши далёкие предки указывали друг другу, сколько охотников нужно, чтобы окружить и загнать зверя. Добыча тоже требовала счёта — нужно было определить, сколько мяса получат члены племени. Так что скоро пяти пальцев стало не хватать. Поэтому древние люди начали считать с помощью камешков и костей, раскладывая их на песке в неверном свете костра.
Однако со временем количество палочек росло, и скоро понадобились обозначения для десятков и сотен. Счёт был нужен, чтобы высчитывать срок появления на свет детей, вести учёт отёла скота и знать, когда взойдут посевы, чтобы предсказывать солнечные и лунные затмения. Также исследователи уверены, что важной вехой в развитии счёта стала торговля. Как объяснить, что пять шкур равны десяти корзинам мяса? Или тридцати мешкам овощей? Появилась необходимость в универсальных обозначениях, а человеческое мышление совершило восхождение к абстракции, обратившись к идее чисел как таковых.
Какие же инструменты помогали человечеству?
Древние люди делали зарубки на костях и камнях и носили эти палочки с собой, либо оставляли чёрточки на стенах жилищ. Одно из самых старинных устройств, которое не так уж далеко ушло от костей на полу пещеры — это, конечно, счёты. По сути они представляют собой те же кости (деревяшки, камушки), только нанизанные на спицы, которые закреплялись в раме.
Их близкий родственник — счётная доска абак, которая появилась в Вавилоне около пяти тысяч лет назад. Очевидно, что её появлению мы обязаны бурной вавилонской торговле. Если классические счёты, какими их знают в России, опираются на позиционную десятичную систему счисления, то вавилонский абак использовал шестидесятеричную. Такой оригинальный способ счёта происходит, как и большинство систем счисления, от пропорций человеческого тела — если говорить точнее, от числа фаланг пальцев на одной руке (не считая большого).
Вариации счётных досок были во всех древних культурах. В Японии они называются соробан, в Китае — суньпань. Римляне делали счёты из металла, передвигая костяшки в пазах металлической доски, а ацтеки — из кукурузных зёрен. Инки использовали для подсчёта зёрен «многоэтажное» устройство под названием юпана.
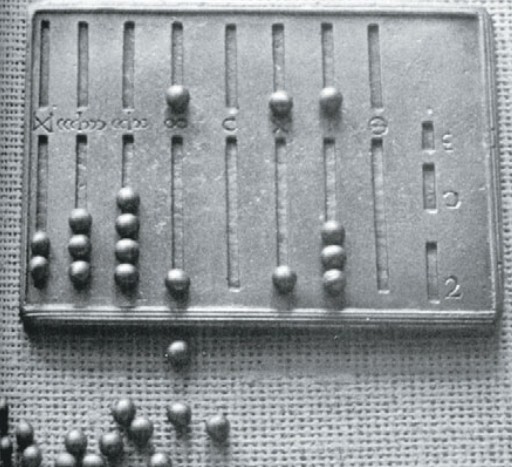
Самые первые помощники человечества в счете
Кость с зарубками, обнаруженная в Дольни-Вестонице. Её возраст — почти 30 000 лет.
Древнеримский абак. Реконструкция
Японские дети собирают соробаны на заводе. 1949 г.
Однако люди всегда стремились упростить себе жизнь, создавая всё более сложные устройства, которые бы взяли необходимость считать на себя. С ростом городов и развитием промышленности потребность в них только увеличилась. В XVII столетии появились логарифмические таблицы и линейки. Шотландский математик Джон Непер изобрёл счётный прибор, известный как палочки Непера. Снискав на время большую популярность, палочки Непера, однако, вскоре были заброшены. А вот арифмометр оказался перспективнее. Изобретённый ещё в античности, в эпоху Просвещения он был переоткрыт и получил заслуженное признание. Ранее схему похожего на арифмометр механизма изображал Леонардо да Винчи, который, как обычно, опередил своё время: тогда его идея успеха не имела.
Как развивались счётные машины?
В общем виде счётная машина представляет собой устройство, работающее на зубчатых колёсах и цилиндрах, которое производит четыре основных математических действия. Записывающие счётные машины также могут автоматически фиксировать результаты на ленте. Принцип счёта основан на поразрядном сложении и сдвиге суммы частных произведений. Свои версии арифмометра создали Блез Паскаль, спроектировавший в 1646 году суммирующую машину «паскалина», и Готфрид Вильгельм Лейбниц: в его арифмометре была ручка, вращение которой ускоряло повторяющиеся операции.
Также следует упомянуть вычислительную машину, разработанную Чарльзом Бэббиджем в XIX столетии. Она могла производить вычисления с точностью до двадцатого знака, подходила для операций с логарифмами и тригонометрическими функциями. Программа для неё была составлена Адой Лавлейс, первой женщиной-программистом, да и вообще первым программистом в мире. Именно ей принадлежат термины «цикл» и «рабочая ячейка».
Арифмометр Блеза Паскаля. 1642 г.
Арифмометр Лейбница. 1673 г.
Элемент аналитической машины Чарльза Бэббиджа. 1910 г.
Существовало множество моделей счётных машин. Например, карманный арифмометр Curta, выпущенный в 1948 году, был размером с человеческий кулак.
В конце XIX века изобретатель Уильям Берроуз запатентовал свой арифмометр и основал компанию по производству компьютерной техники Burroughs Corporation. Его сын продолжил дело, а вот внук, тоже Уильям Берроуз, интересовался литературой куда больше, чем вычислительными машинами, и стал одной из значимых фигур поколения битников.
Арифмометры выпускали марки Facit и Mercedes (не тот, что выпускает автомобили: производитель офисной техники судился с автоконцерном за название, договорившись в результате о том, что у каждой компании своя сфера деятельности). А в СССР самым популярным арифмометром был названный в честь Дзержинского «Феликс», который выпускался заводом «Счётмаш» до 1978 года.
Обладая характерной для механических устройств красотой, арифмометры всё-таки имели существенные недостатки. Порядок действий всегда задавался вручную, поэтому результат счёта сильно зависел от внимательности оператора, которому требовалось нажимать на клавишу для выполнения каждого действия. Арифмометры имели хождение вплоть до второй половины ХХ века, когда их окончательно вытеснили электронные счётные устройства.
Лихтенштейнский карманный арифмометр Curta. 1948 г.
Советский арифмометр «Феликс»
Уильям Берроуз, который любил печатные машинки гораздо больше, чем счётные. 1959 г., Париж. Loomis Dean—Time & Life Pictures/Getty Images
Электронный прорыв
Настоящий прорыв в развитии вычислительной техники случился в 60-х годах ХХ века.
В 1957 году японская компания Casio выпустила первый полностью электронный калькулятор 14-А. Событие было эпохальным, потому что открыло новую эру в мире счёта, но жизнь офисных работников и инженеров эта модель не изменила, ведь весил калькулятор целых 140 кг.
Первым компактным, а значит, массовым, калькулятором стал Anita, выпущенный английской компанией Bell в 1961 году. Он работал на газоразрядных лампах и был оснащён клавишами ввода числа и множителя. С тех пор функции калькуляторов становились всё более серьёзными, а сами калькуляторы — всё более лёгкими и умными.
Например, в 1965 году появился первый настольный электронный калькулятор со встроенной памятью Casio 001. Весил он всего 17 килограмм, что по тем временам для машины, способной запоминать операции, было вовсе не много, а два года спустя появился первый настольный программируемый калькулятор Casio AL-1000.
Однако пользователям калькуляторов было и этого мало, ведь счётное устройство куда удобнее держать в руке и носить с собой. Так появились калькуляторы Sharp и Canon, которые весили менее килограмма.
«Электроника»
Вот ещё несколько эпохальных инноваций от японской марки Casio, которые существенно изменили представления о том, на что способны калькуляторы.
Появился карманный калькулятор Casio Mini, продажи которого побили все рекорды. А через некоторое время компания выпустила миниатюрную версию, Casio Mini Card, размером с кредитную карту.
Компания выпустила калькулятор FX-7000G — первый в мире программируемый графический калькулятор, доступный широкой публике, с матричным дисплеем, имеющем разрешение 96×64 пикселя. Эта модель может отображать как встроенные графики, так и построенные пользователем. В дополнение к режиму графического отображения калькулятор имеет функцию программирования на языке Бейсик.
Пять лет спустя на прилавках появился калькулятор Casio CFX-9800G, в котором впервые появилась возможность делать графики в разных цветах. По сути, был добавлен цветной дисплей. В отличие от современных экранов, он был трёхцветным и работал на отражённом свете. Это дало возможность рисовать каждый график своим цветом, что делало графические отображения функций куда более наглядными.
Casio выпускает устройство CASIO ClassPad 300 — первый калькулятор с большим сенсорным экраном. Модель имела систему компьютерной алгебры (CAS), которая позволяет производить преобразования выражений в аналитической (символьной) форме.
появился калькулятор Casio FX-82ES с технологией Natural Display, позволяющий вводить выражения в естественном виде так, как они выглядят на бумаге. Например, вводить обыкновенные дроби, квадратные корни, экспоненты и логарифмы в виде, принятом в учебниках. В результате сокращается количество ошибок в вычислениях, время вычислений и повышается заинтересованность учеников.
Модель калькулятора Casio fx-CG20 PRIZM явилась развитием первой модели, выпущенной в 2010 году. В отличие от предшественников она имела полноцветный экран высокого разрешения. Модель, несмотря на экран с подсветкой, не потеряла в энергоэффективности и способна месяцами работать на одном комплекте батарей.
Сейчас калькуляторы не только стали компактными и лёгкими, но и освоили массу функций, которые могут быть полезны всем, кому требуются точные и сложные расчёты. Сейчас существуют научные калькуляторы, которым под силу производить вычисления с дробями, считать векторы и матрицы, совершать метрические преобразования и решать уравнения, графические калькуляторы, позволяющие создавать таблицы и строить графики по картинке, а также финансовые калькуляторы, которые справляются с расчётом облигаций и другими нуждами финансиста.
На сегодняшний день флагманская графическая модель — калькулятор Casio FX-CG50 с цветным экраном высокого разрешения, возможностью строить 3D графики, режимом программирования, а также поддержкой векторных и матричных вычислений.
Casio 001. 1965 г.
Casio Mini. 1972 г.
Дисплей калькулятора Casio fX-7000G. 1985 г.
Casio FX-CG50
Так счётное устройство прошло эволюцию от доски с костяшками до маленького мощного компьютера, сохранив, тем не менее, главное свойство — способность облегчать жизнь человеку, освобождая его разум для стратегических решений.
Как человечество считало деньги
Приглашаем в исторический экскурс. Следуй за нами, читатель, и ты узнаешь, как зародились, эволюционировали и ассимилировались с происходящими социальными процессами счетные системы.
На пальцах
Первые счетные системы человек, вероятно, начал использовать в эпоху позднего палеолита (40–12 тысяч лет назад). Простейшими инструментами для этого служили пальцы. Счет на пальцах широко применялся в Древнем мире и Средневековье, постепенно совершенствуясь и усложняясь.
Естественное распределение пальцев на руках и ногах привело к использованию нескольких разрядов при счете и появлению нескольких систем счисления. Десятеричная система возобладала у народов Евразии. Пятеричная долгое время применялась в Китае, Древней Греции (аттическая система счисления, вытесненная затем десятеричной ионической), Древнем Риме и среди племен тропической Африки. Двадцатеричная система была у ацтеков и майя. Использование при счете четырех пальцев двух рук (большой палец не считался) привело к появлению восьмеричной системы счисления.
В древнем Шумере возникла двенадцатеричная система счисления, в которой счет велся по фалангам четырех пальцев руки. Элементы этой системы еще длительное время использовались в различные периоды истории во многих странах. Так, в Древнем Риме либра (мера веса) равнялась 12 унциям. Введенное денежной реформой Карла Великого (VIII век) соотношение «1 шиллинг = 12 денариев» просуществовало в денежных системах различных государств много столетий. Последними странами, отказавшимися от унаследованного от каролингской реформы соотношения (1 фунт = 20 шиллингов = 240 пенсов), были Великобритания (1971 год) и Нигерия (1973 год). В Древней Руси счет «дюжинами» (большим пальцем руки по фалангам остальных четырех пальцев) применялся в торговле, особенно в Новгороде в XII–XV веках, а традиция считать некоторые товары (носовые платки, карандаши и другие) дюжинами сохранялась до начала XX века.
Ловкость рук и никакого мошенничества
В период Римской республики активная международная торговля, в которую были вовлечены Средиземноморье и Ближний Восток, дала толчок развитию пальцевого счета. С его помощью можно было показывать числа до 10 000, а с использованием других частей тела — до миллиона. Римский ритор Квинтилиан (I век) писал, что необразованного человека выдает неумение правильно показать числа на пальцах.
В различных районах мира применялись системы пальцевого счета, отличные от римской. Так, арабские торговцы, знакомые с описанной Бедой Достопочтенным системой счета, применяли и отличавшийся от нее арабско-восточноафриканский метод. Собственная система счета, с помощью которой можно было показать числа до 100 миллионов, существовала в Китае.
Посчитать предметно
Счет на пальцах имел множество достоинств: простота, компактность, «счетные приспособления» всегда при себе. Но были у него и недостатки: для фиксирования результатов приходилось прибегать к иным средствам. Использование для счета других предметов (камней, раковин, костей, палочек и так далее) позволяло устранить этот недостаток. Счет мог вестись с помощью одновременно как пальцев, так и предметов.
Считать большие числа с помощью предметов было затруднительно, поэтому, например, при счете на палочках могли использоваться либо палочки разного цвета, либо различное положение палочек (горизонтальное или вертикальное) для обозначения разных разрядов.
В Древнем Китае возникшая в эпоху Сражающихся царств (V век до нашей эры) система счета на палочках использовалась до эпохи династии Мин (XIV–XVII века). Наибольшее развитие китайские счетные палочки получили в период династий Сун (X–XIII века) и Юань (XIII–XIV века). Применение китайских счетных палочек позволяло оперировать огромными числами и производить различные действия (сложение, вычитание, умножение, деление, действия с дробями и отрицательными числами, извлечение квадратного и кубического корня). Китайский математик Чжу Шицзе (1249–1314 годы) описал также способы решения с помощью палочек алгебраических уравнений.
Заруби себе на носу
Для фиксации результатов счета стали широко применяться отметки на различных предметах: зарубки (насечки), нанесение полос краской, завязывание узелков. Известно довольно много находок костей с нанесенными на них зарубками: предметы, относящиеся к эпохе мустьерской культуры (около 50 тысяч лет назад, департамент Дордонь во Франции), кости с нарезками из Дольни-Вестонице (около 30 тысяч лет назад, Чехия), браслеты с насечками, относящиеся к мезинской культуре (около 25–30 тысяч лет назад, Черниговская область) и другие. Нет единой точки зрения, имеют ли эти зарубки декоративный или счетный характер.
В Англии использование бирок было узаконено около 1100 года при короле Генрихе I (1068–1135 года) и отменено только в 1826 году. Вплоть до конца XVIII века бирки служили для учета уплаты налогов.
Законодательством Российской империи предусматривалось применение бирок для различных целей. Так, Местное Великороссийское Положение допускало учет с помощью бирок отработанных крестьянами в пользу помещика дней, а Устав торгового судопроизводства 1887 года признавал бирки особым родом доказательств, применяемых в торговом быту.
Узелок завяжется, узелок развяжется
Различные системы для счета с помощью узелков существовали у разных народов — китайцев, персов, индийцев и других. Эта система упоминается в трудах греческого историка Геродота (V век до нашей эры). Древнекитайский философ Лао-цзы (VI–V век до нашей эры) писал об употреблении веревок и узлов для счета как об основательно забытом обычае.
Наивысшей степени развития узелковое письмо достигло в Южной Америке в эпоху расцвета государства инков (XV век). Система инков, называвшаяся «кипу», представляла собой сложные веревочные сплетения и узлы, которые могли содержать различное количество свисающих нитей — от нескольких штук до более полутора тысяч.
С помощью кипу не только проводились арифметические вычисления, но и велось исчисление времени, делались картографические описания, записывались законы и генеалогические сведения, передавались донесения, велся бухгалтерский учет. Читали кипу специально подготовленные профессионалы — «кипукумайоки».
Через полвека после уничтожения государства инков конкистадорами (1532–1533 годы) колониальные власти запретили кипу, но использование этой счетной системы в некоторых районах продолжалось до начала XX века.
Взвешенное решение
С древности своеобразным счетным устройством служили человеку весы (древнейшие весы были обнаружены археологами в Месопотамии и относятся к V тысячелетию до нашей эры). Их применяли для определения количества однородных предметов путем взвешивания вместо пересчета. Неслучайно названия некоторых денежных единиц как в период античности (мина, либральный асс), так и в более позднее время (фунт, французский ливр, итальянская лира) происходят от единиц измерения веса. Чеканившиеся в СССР с 1926 по 1991 годы монеты в 1, 2, 3 и 5 копеек имели вес соответственно в 1, 2, 3 и 5 граммов, что позволяло определять сумму большого числа монет простым взвешиванием.
Важным этапом развития в древности стало появление счетных досок, получивших общее название «абак». Происхождение этого термина не установлено. Возможно, греческое слово ἄβαξ происходит от общесемитского корня слов со значением «пыль». Такое название могло быть связано с тем, что для вычислений использовались доски с углублениями и линиями, на которых в определенном порядке раскладывались однородные предметы (камешки, кости и другие), а чтобы они не скатывались с доски, она покрывалась слоем песка. Считается, что раньше, чем в Греции, абак стали применять в Вавилоне, Египте и Финикии, но археологических подтверждений этому пока не обнаружено. Пифагор (VI век до нашей эры) полагал, что счет с помощью абака должен входить в курс математики.
В Древнем Риме абак появился, вероятно, в V–VI веках и назывался calculi и abaculi (abacus). Римские абаки изготавливались из различных материалов (бронза, слоновая кость, цветное стекло). Бронзовый римский абак, хранящийся в Национальном археологическом музее Неаполя, представляет собой доску с прорезанными в ней щелями, в которых перемещаются костяшки. Семь длинных щелей с четырьмя костяшками, одна — с пятью, над каждой длинной щелью — короткая с одной костяшкой. Над длинными щелями помечены значения разрядов: миллионы, сотни тысяч, десятки тысяч, тысячи, сотни, десятки, единицы, унции (то есть двенадцатые части). В щели, помеченной « », — пять костяшек (то есть 5/12). В правой части абака — щели с пометками, означающие 1/2, 1/4 и 1/6 унции.
Распад и падение Римского государства прервали развитие счетной техники. Абак в Европе был надолго забыт.
В Китае аналог абака — суаньпань — появился в VI веке и постепенно вытеснил традиционную систему счета на палочках. Со временем его устройство менялось, современный вид он приобрел в XVII веке. Суаньпань представляет собой прямоугольную раму, разделенную на две части. В большом отделении («Земля») на каждой проволоке — 5 шариков, в меньшем («Небо») — 2 шарика. Проволоки соответствуют десятичным разрядам, каждый шарик большего поля — единице, меньшего — пяти. На суаньпане можно не только производить четыре арифметических операции, но и извлекать квадратные и кубические корни.
В XV–XVI веках суаньпань был завезен в Японию, где получил название «соробан». В Японии он был модифицирован (последний раз — в 1930 году).
Абак, забытый в Европе после распада Римской империи, вновь получил распространение в X веке благодаря монаху Герберту Орильякскому (938–1003), ставшему впоследствии римским папой Сильвестром II. Герберт во время путешествия в Кордовский халифат познакомился с арабской системой цифр и с абаком.
В XV веке в Англии появилась новая форма абака — «счет на линиях», — распространившаяся в XV–XVI веках по континентальной Европе. Для счета на линиях использовались горизонтально разлинованная доска и металлические жетоны, которые в Германии назывались счетными пфеннигами, в других странах — фишками. Жетоны при счете выкладывались не только на линиях, но и между ними. Разрядность повышалась снизу вверх. Правила счета на линиях излагались во многих учебниках, изданных в XV–XVII веках, счет упоминается в созданных в то время пьесах Шекспира и Мольера.
Лечь костьми
Немецкий физик, математик и философ Готфрид Лейбниц (1646–1716 годы) предпочитал счет на линиях счету на бумаге. Постепенно первый уступал последнему, применяясь все реже. Дольше всего он сохранялся в Германии и Австрии — до конца XVIII века.
Счетные приборы, аналогичные абаку, существовали в Америке. Так, в государстве инков применялись несколько видов устройства, называвшегося «юпана». Для вычислений применялись зерна, которые раскладывались по ячейкам.
В России существовал аналогичный счету на линиях способ, называвшийся «счет костьми». Он описан в рукописных книгах XVI века, объединенных общим названием «Цифирная счетная мудрость», но возник задолго до этого. Свое название способ получил из-за использования для счета сливовых или вишневых косточек. Внешне приспособление напоминало европейскую доску для счета на линиях. Горизонтальные линии служили разделителями разрядов. Косточки на линиях обозначали единицы разряда, кость над линиями — пять единиц разряда. Иногда для счета служили металлические жетоны («пенязи», что дало второе название — «счет пенязями»). Для вычисления налогов на досках применялись добавочные разделения для подсчета трети (1/3), полутрети (1/6) и так далее до «малой чети» (1/32).
В XVI веке на смену счету костьми пришел более удобный «дощаный счет». Его полное описание содержится в списке «Счетной мудрости» 1691 года. Первоначально устройство для дощаного счета представляло собой два соединенных ящика, каждый из которых был разделен на два отделения. Наличие четырех отделений позволяло не только сохранять условие задачи, но и фиксировать промежуточные расчеты. В каждом отделении было натянуто по 14 веревочек с нанизанными на них костяшками. На верхних десяти было по 9 костяшек (иногда — по 10), они предназначались для операций с целыми числами. На нижних рядах, содержащих 3, 4, 5 или 6 косточек, производились операции с дробями. Ряды с одной или двумя костяшками представляли половину той дроби, под которой они находились.
Постепенно устройство дощаного счета совершенствовалось, в нем стали применяться только две части вместо четырех, и только нижние ряды, для работы с дробями, имели четыре отделения. Затем исчезли ряды, содержащие по одной костяшке.
В XVII веке меняется название прибора, в 1658 году «счоты» впервые упоминаются в «Переписной книге домовой казны патриарха Никона». В начале XVIII столетия дощаный счет в России окончательно трансформируется в «счеты», в дальнейшем претерпевая только незначительные внешние изменения. В XIX веке русские счеты стали известны в Западной Европе, однако использовались там только для обучения в начальной школе. В России они применялись в торговле и бухгалтерском учете до конца XX века, пока не были окончательно вытеснены калькуляторами. В начальной школе для обучения счету они служили до конца 1980-х годов.
В счетах применяется позиционная десятичная система счисления. Каждый ряд костяшек представляет собой числовой разряд, возрастающий от единиц до сотен тысяч, а вниз — уменьшающийся от десятых до тысячных. Прут с четырьмя костяшками служит разделителем целых и дробных частей, а также для счета полушками (1/4 копейки).
Палочки на новый лад
Палочки неоднократно пытались усовершенствовать. Первую попытку предпринял сам Непер. В приложениях к «Рабдологии» он дал описание прибора, состоящего из 200 палочек, и счетной доски. Однако эти его изобретения были чрезвычайно сложны и не нашли практического применения.
Более удачными усовершенствованиями палочек Непера были предложенные русским изобретателем Г. К. Иоффе в 1881 году («бруски Иоффе») и французскими инженером А. Женаем и математиком Э. Люка в 1891-м («бруски Женая — Люка»). Бруски Женая — Люка позволяли выполнять умножение любого натурального числа на любое натуральное число, при этом пользователь, представляя перенос графически, мог считывать результат умножения без промежуточных расчетов. Принцип действия брусков Иоффе был основан на теореме Слонимского и позволял производить умножение быстрее. Популярность брусков для вычислений оказалась недолгой: вскоре они были вытеснены механическими вычислительными устройствами.
Механические расчеты
В связи с распространением торговых операций и океаническим судоходством возникла потребность в автоматических вычислениях. В двухтомном собрании рукописей итальянского ученого Леонардо да Винчи (XV–XVI век) содержится описание 13-разрядного суммирующего устройства, состоящего из стержней, на которые крепятся два зубчатых колеса: с одной стороны — большее, с другой — меньшее. Суммирующая машина Леонардо да Винчи, однако, так и осталась одним из нереализованных его проектов.
В 1623 году немецкий ученый Вильгельм Шиккард (1592–1635) разработал машину, названную им «счетные часы» и предназначенную для суммирования и умножения шестизначных чисел. Машина Шиккарда состояла из суммирующего устройства, множительного устройства и устройства для записи промежуточных результатов. Устройство было шестиразрядным, в каждом разряде на оси имелись закрепленная шестеренка с десятью зубцами и колесо с одним «пальцем», служившим для передачи десятка в следующий разряд. Были изготовлены два экземпляра машины Шиккарда, однако оба они сгорели во время пожара.
Машины Леонардо да Винчи и Шиккарда были забыты, поэтому длительное время считалось, что создателем первой арифметической машины является французский ученый Блез Паскаль (1623–1662). В 1960-х годах были изготовлены машины Леонардо и Шиккарда, доказавшие свою работоспособность.
Первая модель суммирующей машины Паскаля была создана в 1642 году. В дальнейшем изобретатель неоднократно ее совершенствовал, экспериментируя с материалами и формой деталей. Всего Паскаль создал более 50 моделей машины, названной «Паскалина», из них сохранилось восемь. Машина представляла собой небольшой ящичек с восемью круглыми отверстиями и нанесенной вокруг них круговой шкалой. Шкала крайнего правого отверстия была разделена на 12 частей, соседнего с ним — на 20, остальных — на 10. Такая градуировка была связана с тем, что Паскаль создавал свою машину в помощь отцу, сборщику налогов, и поэтому она соответствовала тогдашней монетной системе (1 ливр = 20 су = 240 денье). В отверстиях располагались зубчатые колеса, число зубьев колеса соответствовало числу делений шкалы данного отверстия. Один из зубцов каждой шестерни был немного удлинен и задевал соседнее колесо. «Паскалина» не получила широкого распространения в связи с ее высокой стоимостью, а также с незначительными вычислительными способностями — в частности, с неудобством выполнения операций вычитания.
В 1673 году Готфрид Лейбниц создал «ступенчатый вычислитель». В основе арифмометра Лейбница лежит ступенчатый валик (или колесо Лейбница), который впоследствии использовался в конструкции вычислительных машин на протяжении трехсот лет. Ступенчатый валик представлял собой цилиндр с зубцами разной длины, которые взаимодействуют со счётным колесом. Передвигая колесо вдоль валика, его вводили в зацепление с необходимым числом зубцов и обеспечивали установку определённой цифры. Механизм ввода слагаемых находился на подвижной каретке. Конструкция арифмометра включала две вращающиеся рукоятки: одна — для сдвига подвижной каретки, другая — для вращения ступенчатого колеса, что позволяло ускорить повторяющиеся операции сложения, при помощи которых выполнялись умножение и деление. Машина работала с 12-разрядными числами, позволяла производить операции сложения, вычитания, умножения, деления и извлечения квадратного корня.
Появившиеся в XVII–XVIII веках модели арифмометров не нашли широкого распространения, оставшись в основном в виде демонстрационных моделей.
Век арифмометров
В ходе промышленной революции XIX столетия потребность в механизации счетных работ стала возрастать. В 1820 году появляется «арифмометр Томаса», ставший первым серийно производимым арифмометром. Французский предприниматель Шарль Ксавье Тома де Кольмар (1785-1870) создает свой арифмометр, основанный на принципе Лейбница. Де Кольмар неоднократно выставлял свой арифмометр на различных международных выставках, и хотя его прибор не получил ни одной награды, он намного превзошел по продажам устройства всех остальных изобретателей. Арифмометр продавался в количестве 300–400 экземпляров в год (для того времени — довольно массовый выпуск) вплоть до начала прошлого столетия, то есть почти 90 лет.
В конце XIX века предпринимались также попытки выпуска арифмометра Томаса под иными марками, с внесенными в конструкцию изменениями. В 1874 году шведско-русский инженер Вильгодт Теофил Однер создал новую модель, основанную на применении «колеса Однера» — зубчатки с переменным числом зубцов. В его конструкции колесо имеет 9 выдвижных спиц. Количество выдвинутых спиц определяется углом поворота установочного рычажка до соответствующей цифры на шкале. Колесо Однера оказалось настолько удачным, что без принципиальных изменений применялось во многих последующих моделях арифмометров. В 1877 году на заводе Нобеля был выпущен первый арифмометр Однера, а в 1890 году его производство началось на фабрике Однера — Гиля в Петербурге. В 1897-м Однер стал единоличным владельцем фабрики, после его смерти производство продолжила фирма под названием «Наследники Однера». После Октябрьской революции завод был национализирован, а производство арифмометров прекращено. В 1925 году оно возобновилось на Сущевском заводе имени Дзержинского под прежней маркой «Однер», а с 1931 по 1978 год — «Феликс». Наследники Однера, эмигрировавшие после революции в Швецию, создали там новое производство и стали выпускать арифмометры под маркой «Оригинал-Однер».
Счетные машины типа Однера имели определенные недостатки: постановка рычажков на нужные цифры, обратная их перестановка, движение каретки и вращение барабана производились вручную. В XX веке появились вычислительные машины с электроприводом, в которых вращение барабана и передвижение каретки производилось электродвигателем, а набор чисел выполнялся нажатием клавиш. Это позволяло существенно повысить скорость вычислений по сравнению со счетом на арифмометрах с ручным приводом. Результаты вычислений фиксировались в виде цифр на барабанах, а в некоторых моделях (счетно-записывающих машинах), кроме того, печатались на бумажной ленте, причем могли воспроизводиться не только окончательные, но и промежуточные результаты.