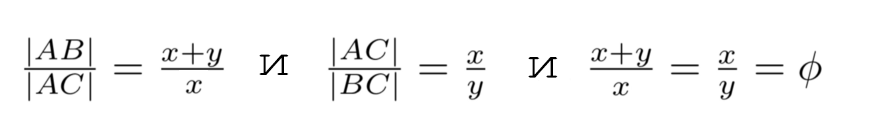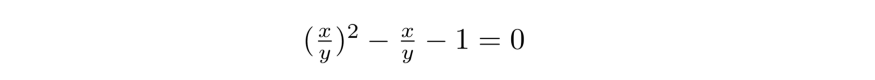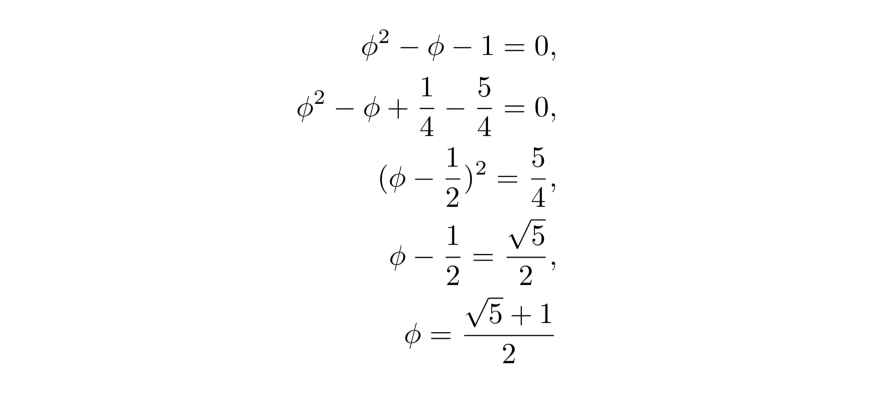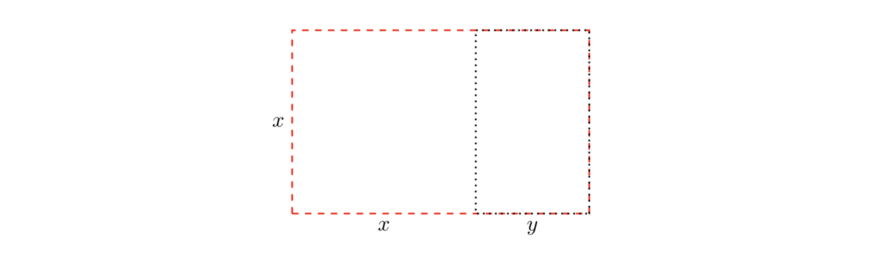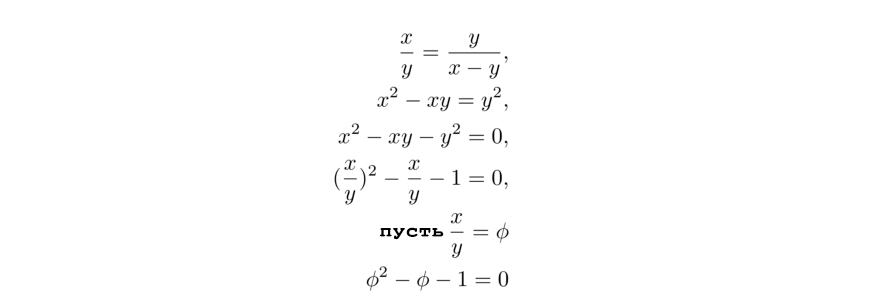Что можно что нельзя объяснить числами
Философия и числа
( конструктивная философия)
1. Философия – наука, которая занимается наиболее общими вопросами. Число – самое обобщенное научное понятие. Интересно найти между ними связь, то общее, что их объединяет.
Первично разделение единой природы на материю и сознание, они одновременны. Они взаимодействуют в рамках единого энергоинформационного поля, а их разделение необходимо методически в рамках философии (мысль нематериальна). Но мысль должна иметь материальный носитель (например, ячейка памяти), а строгое следование материи определенным законам (например, законам Ньютона ) можно рассматривать, как элемент самосознания.
3. Следующий этап познания – сравнение. В конструктивной философии постулируется, что сравнивать можно только числа. Поэтому на первом этапе сравнения надо получить числовой эквивалент того, что сравнивается. Получение числового эквивалента, по сути является измерением. Таким образом, чтобы сравнить, надо сначала измерить. Числовые эквиваленты для сравнения следует вычитать, а не делить, чтобы не возникало проблемы деления на ноль. Следует отметить, что сравнение по типу больше, меньше также является измерением, причем в качестве единицы измерения выступает один из сравниваемых объектов.
4. В результате измерения получается числовой эквивалент, но не просто число, а число, имеющее размерность единицы измерения. Сравнивать можно только числовые эквиваленты, имеющие одинаковую размерность. Например, единица измерения длины – метр, а времени – секунда.
5. Для конструктивной философии важно, что измерять можно только тогда, когда есть единица измерения.
Физические величины имеют физические единицы измерения, а философские понятия для сравнения должны иметь философские единицы измерения. В некоторых случаях философская и физическая единицы измерения могут совпадать.
Физической единицей для сознания может служить бит информации, а для материи – единица энергии или массы. Трудно сказать, что представляют собой философские единицы для материи и сознания, но принципиально важно, что это разные единицы, поскольку в философском плане мысль нематериальна. Следовательно, в принципе не может быть одной и той же единицы измерения для сознания и материи.
Философская единица измерения аналогична кванту в квантовой механике, поэтому не может быть дробных долей в результат измерения. В частном случае в качестве философской единицы измерения может выступать физическая единица измерения, но результат измерения в философских единицах должен быть целым числом.
Чтобы получить единицы измерения для каких-либо бесконечномерных понятий, например, добро или зло, можно применить метод раскрытия неопределенностей вида бесконечность, деленная на бесконечность. В этом случае
в качестве единицы измерения берется другое бесконечномерное понятие, а их отношение оказывается конечным числом.
Например, в фигурном катании бесконечномерная величина – выступление фигуриста оценивается с помощью другой бесконечномерной величины – мнения судьи. В результате отношения судьи к выступлению фигуриста появляется оценка, то есть конечное число, выраженное в баллах. Другой очевидный пример – школьные оценки – баллы успеваемости.
При таком подходе зло можно оценить сроком, предусмотренным приговором суда. Добро можно оценить временем, в течение которого его помнят. И в том и в другом случае результат будет выражен в годах.
Но баллы, годы – это искусственные приемы, конструктивная философия постулирует, что единица измерения существует объективно и формируется в процессе диалектического развития. Принцип тезис – антитезис – синтез можно отнести и к процессу формирования единицы измерения, но диалектика – это отдельная область.
6. Следует отметить, что не все числа можно сравнивать. Например, для комплексных чисел отсутствует понятие больше или меньше. Комплексное число содержит две составляющие – действительную и мнимую, у которых нет общей единицы измерения, поэтому в целом комплексные числа нельзя сравнивать.
По аналогии с комплексными числами философские числа для материи можно считать действительными, а для сознания – мнимыми. В этом случае любому явлению или понятию должно соответствовать некоторое комплексное число. Физической основой двух видов чисел может служить наличие в природе двух видов движения: поступательного ( действительные числа ) и вращательного ( мнимые ).
7. Конструктивная философия рассматривает развитие, как движение по натуральному ряду чисел в сторону увеличения. Процесс развития, как и время, однонаправлен. В процессе непрерывного развития единица измерения сохраняется, и этим движение по натуральному ряду напоминает движение во времени.
Но движение по натуральному ряду – это не стремление к “дурной бесконечности”. В процессе развития встречаются простые числа. Появление простого числа означает качественное изменение. Простые числа чаще встречаются в начале натурального ряда, поэтому в начале качественные изменения чаще и жить, как говорится, интереснее. Периодическое появление одних и тех же сомножителей соответствует развитию по спирали.
Кроме того, в принципе возможны революционные скачки, вызванные изменением единицы измерения. Изменение единицы измерения связано с процессами в единой природе, которые не учитываются при разделении на материю и сознание. Философский постулат состоит в том, что невозможно объять необъятное. Весь вопрос в том, как это учесть, выработав алгоритм познания.
Предлагается принципиально допустить возможность изменения единицы измерения. Существенно, что старая и новая единицы измерения несоизмеримы, поэтому состояния до и после скачка нельзя сравнивать. Область, в которой происходит скачок, обычно ограничена, например, областью какой–либо науки, либо жизнью одного человека : детство, зрелость, старость.
Но конструктивная философия допускает скачки в любой области познания даже самой широкой. Следовательно, возможны скачки в развитии материи или в развитии сознания.
Примером физического процесса, который следует натуральному ряду, может служить расширение Вселенной. С точки зрения философии оно ничем не ограниченно, так как нет самого большого числа. С точки зрения физики оно может смениться сжатием. В рамках философии такой переход будет означать скачок и изменение единицы измерения. Причина смены расширения на сжатие, конечно, физическая, а философия определяет методику изучения этого процесса.
Поскольку в натуральном ряде нет наибольшего числа и нет наибольшего простого числа, то возможно развитие без “ дурной бесконечности” и без изменения единицы измерения, то есть без революции. Но бесконечность природы проявляет себя в неожиданных скачках, с этим же связан вероятностный характер физических процессов. Вероятность и революция – диалектическая противоположность движению по натуральному ряду.
8. Придание числам философского смысла известно со времен Пифагора. В практической жизни некоторые числа прочно ассоциируются с определенными понятиями.
Специально рассмотрим число ноль. Это не отсутствие числа, а именно число. Значит, как число, оно должно нечто обозначать. Предположим, что ноль обозначает нечто, не имеющее единицы измерения, как остальные числа. Для чисел натурального ряда единица измерения – это просто единица натурального ряда. Кроме того, каждое число можно считать единицей измерения самого себя, поскольку при делении числа самого на себя получается единица так же, как при делении единицы измерения самой на себя. Если число содержит несколько сомножителей, то любой из них можно считать единицей измерения этого числа.
Ноль не может быть единицей измерения для других чисел, поскольку делить на ноль нельзя, важно отметить, что ноль также нельзя делить на ноль, и поэтому ноль не может быть единицей измерения самого себя. Таким образом, запрет деления на ноль имеет абсолютный приоритет. Если бы можно было делить ноль на ноль, то это отношение должно было равняться единице, поскольку ноль – число. Раскрытие неопределенности вида ноль, деленный на ноль, к натуральному ряду не относится, так как в нем только целые числа. При делении числа на единицу измерения этого числа должно обязательно получаться только целое число, нецелые числа не являются членами натурального ряда. Конструктивная философия также рассматривает только целые числа, используя свойства натурального ряда для философских построений.
Известно, что единица, деленная на ноль, часто обозначается знаком бесконечность, но поскольку делить на ноль нельзя, то не может быть никакого числового результата. Поэтому бесконечность не является числом, а только знаком для обозначения дроби вида единица, деленная на ноль. Такой подход логичен еще и потому, что не существует самого большого числа, а бесконечность ассоциируется с чем-то самым большим.
Физическим аналогом нуля является вакуум, это не отсутствие материи, а по современным представлениям среда, в которой образуются виртуальные частицы и которая обладает огромным энергетическим потенциалом.
9. Важный философский вопрос – это вопрос о существовании бога. Если учесть, что бог един, то он должен объединять сознание и материю, тогда в качестве бога можно принять единую природу, которую в начале познания надо разделять на сознание и материю. При таком подходе разделение на сознание и материю в принципе не может быть полным, следовательно, всегда остается возможность чуда. С другой стороны, любое чудо может быть в принципе объяснено. Кратко можно сформулировать так. Бог есть, но он равен нулю, причем ноль – это число, а не отсутствие числа, “ делить ” на бога нельзя, его надо “ уважать “.
10. Чем конкретно может быть полезна конструктивная философия? Прежде всего, она дает алгоритм познания: разделение, измерение, сравнение. Вместо того чтобы спорить о вечных истинах и выяснять, что первично материя или сознание, конструктивная философия направляет познание в русло конкретных измерений. К сожалению пока неясно, как объективно определить философскую единицу измерения и философское число (не путать с философским камнем). Для конкретных наук философскими числами могут служить установившиеся понятия. Например, в химии это может быть номер элемента в таблице Менделеева. Философские числа должны быть только целыми.
Но основным методом получения философских чисел пока остается метод баллов. Несмотря на свою субъективность, он позволяет выявлять несоизмеримые величины и понятия. Если какие-то понятия нельзя оценить с помощью одного и того же балла, то они несоизмеримы, и, следовательно, их нельзя сравнивать так же, как, например, действительные и мнимые числа.
Принципы конструктивной философии аналогичны принципам конструктивной математики. Это, а также обращение к числам, дает шанс на решение некоторых философских задач с помощью компьютера.
Явления, которые не может объяснить математика
Думаете, математика поможет решить все задачи и вопросы? А вот и нет! Смотрите, как она не справляется с толкованием некоторых вещей.
Даже математика не в силах объяснить отдельные невероятные явления. Предпочитаю называть эти вещи «Абракадаброй математики». В разработке тоже встречаются подобные загадки.
Изложенная информация будет наиболее интересна фронтендерам и заядлым любителям математики 😉
Любимое число
Давайте посмотрим на один такой трюк. Предположим, что вы учитесь в классе с численностью не менее 25 студентов, а я преподаватель. Даю каждому чистый лист бумаги и прошу написать цифру от 0 до 9 включительно. Когда вы справитесь и свернёте листок, соберу бумаги. Само собой, я не в курсе, что вы придумали. Тем не менее гарантирую, что буду знать число, которое встречается чаще других в ответах аудитории.
Теперь утверждаю, что большинство студентов выбрали цифру 7. Если учащийся придёт, посмотрит все листки и проверит, то скажет: «Вы правы! Но как?»
К сожалению, нет никакого объяснения такой закономерности, хотя она железная. Большинство людей всегда делают выбор в пользу цифры 7. Я мог сыграть в эту игру свыше 100 раз, и никогда бы не ошибся.
О данном фокусе мне рассказал один любимый профессор, Али Несин, 10 лет назад. Чтобы попробовать трюк, соблюдайте некоторые условия. Перво-наперво нужно как минимум 25 человек. В противном случае будет рискованно. Вы подумаете, что речь идёт о вероятности, но на самом деле это не так. Поскольку в задании 10 цифр, вероятность выбора любой составляет 1/10 для каждого учащегося. Итак, математическое толкование не работает здесь. Думаю, что это объясняется физиологией или социологией.
Красота
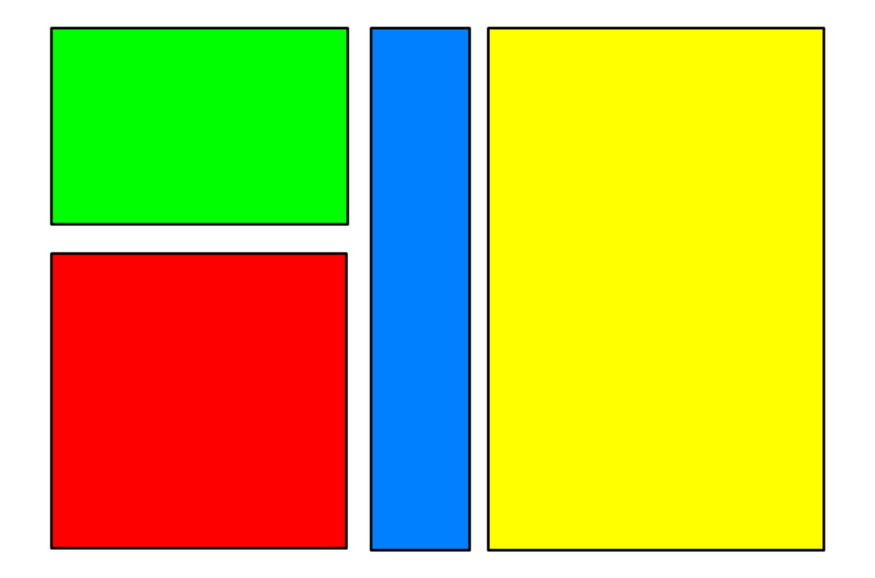
А также математика не способна истолковать другую чрезвычайно занимательную вещь. Здесь 4 разных прямоугольника. Спросите людей, какой красивее, и 70–80% выберут зелёный.
При этом не получится объяснить положение с использованием только математики, потому что в ней нет определения красоты, и этот факт математически непостижим. Впрочем, маркетологи использовали данную информацию вовсю. Когда поняли, что основная масса людей предпочитает определённый дизайн.
Спустя много лет мы так и не нашли ответ, почему люди выбирают число 7, но академик Адриан Беджан разобрался в причине выбора зелёного прямоугольника. Профессор обнаружил, что «человеческий глаз способен интерпретировать изображение на основе золотого сечения быстрее, чем любое другое».Таким образом, благодаря гармоничному делению прямоугольник зелёного цвета и выглядит красивее остальных фигур.
Вероятно, вы слышали об Евклиде. Этот математик написал книгу под названием «Элементы». Однозначно рекомендую вам купить том. В труде Евклид определил золотое сечение следующим образом:
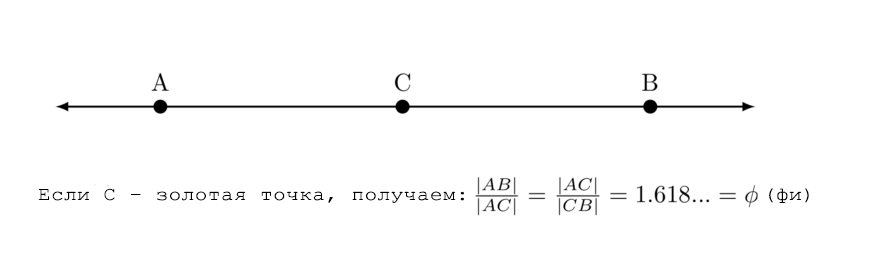
Разделите прямую линию в крайнем и среднем отношении так, чтобы целая линия относилась к большему отрезку, как больший к меньшему.
Другими словами, Евклид говорил: на отрезке стоит точка, назовём её золотой, которая идеально разделяет линию. Он утверждал уверенно, но также и правдиво.
Уверен, что эта специальная пропорция вызывает море любопытства, и вам не терпится узнать, как Евклид получил значение золотого сечения? Давайте попробуем понять вместе.
Пока что работали над отрезком. До сих пор готовимся показать, почему люди выбирают зелёный прямоугольник выше и на каком основании Евклид назвал его золотым.
Золотой прямоугольник отличает свойство, которого нет ни у одного прямоугольника. В чём исключительность: если вырезать из него квадратную часть, оставшийся прямоугольник также золотой. Пусть это будет вам в качестве упражнения!
Непревзойдённый треугольник
Это ещё куда ни шло. Теперь попробуем другую задачу. Например, найти золотой треугольник, если такой существует.
Сначала решим, какой тип нужен для работы. Помните, когда удаляем квадратную часть из золотого прямоугольника, по-прежнему остаётся золотой прямоугольник. Нужно то же свойство для треугольников. Думаю, очевидно, что равносторонний не подходит, потому как при вырезании равностороннего треугольника из равностороннего треугольника остальная часть не будет такой же фигурой.
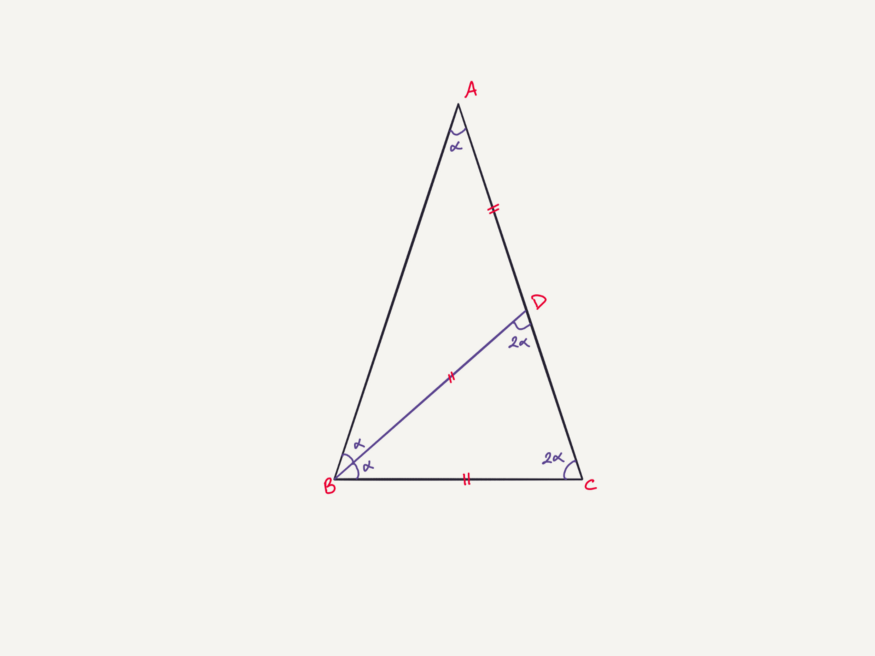
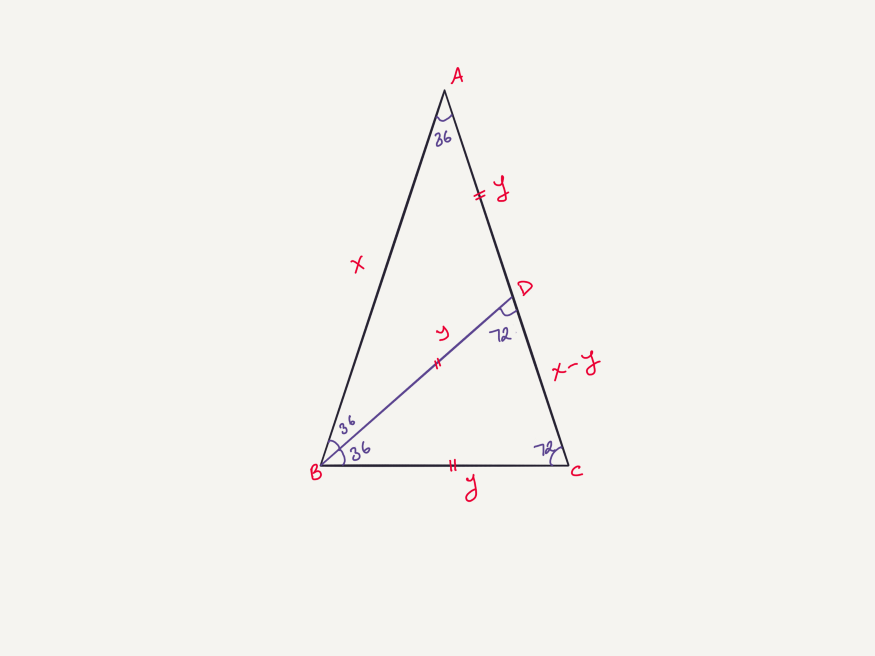
Тем не менее порадую тем, что возьмём равнобедренный треугольник. Шаги понятны. Берём его, а затем вырежем ещё один равнобедренный треугольник из нашего исходного, и проверим, будет ли оставшийся похож на первоначальный или нет. Если да, сделаем попытку назвать его золотым. А попробуем, потому что следующим шагом будет поиск соотношения сторон, равного золотому сечению.
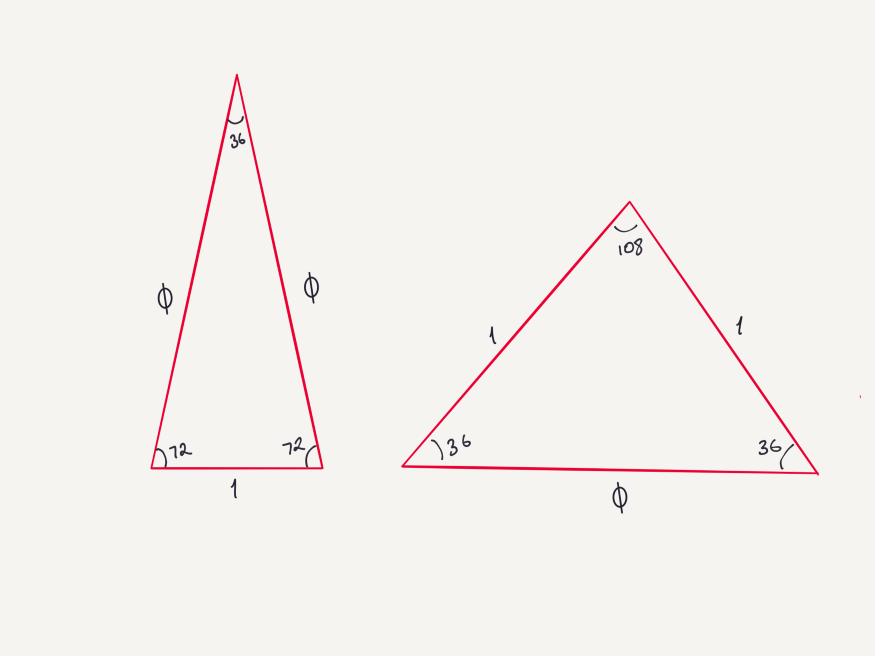
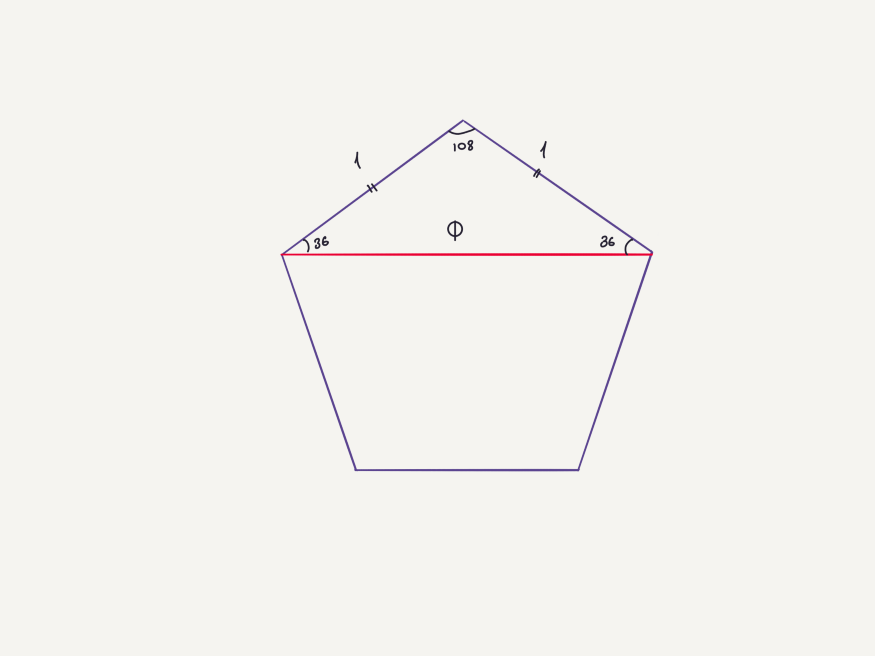
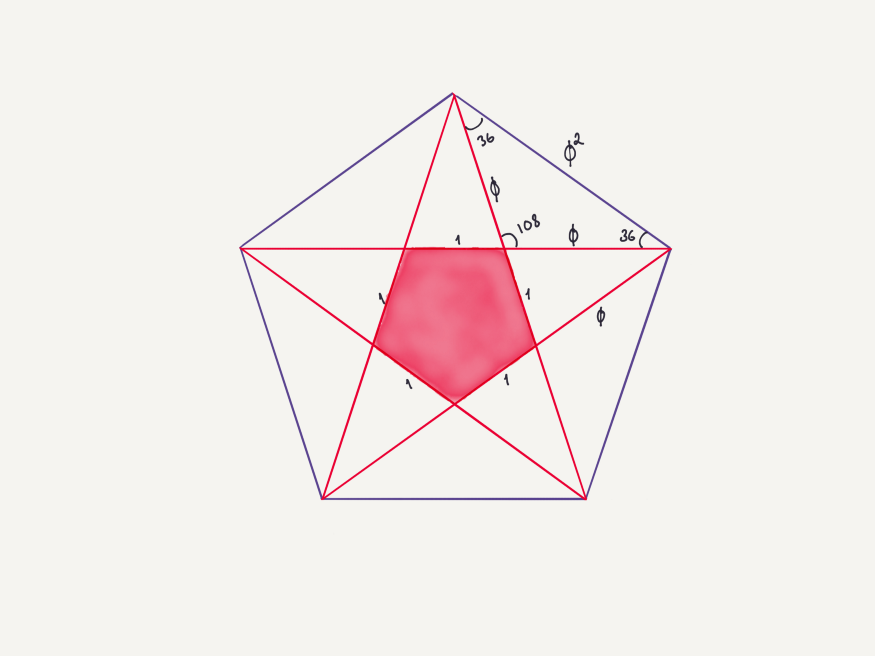
Как видите, получаем то же квадратное уравнение в конце. Таким образом, треугольник с углами 36–72–72 заслуживает названия «золотой». Кстати, когда продолжите углубляться, вы увидите, что 108–36–36 – также золотой треугольник. Эта информация будет полезна при работе с пятиугольником.
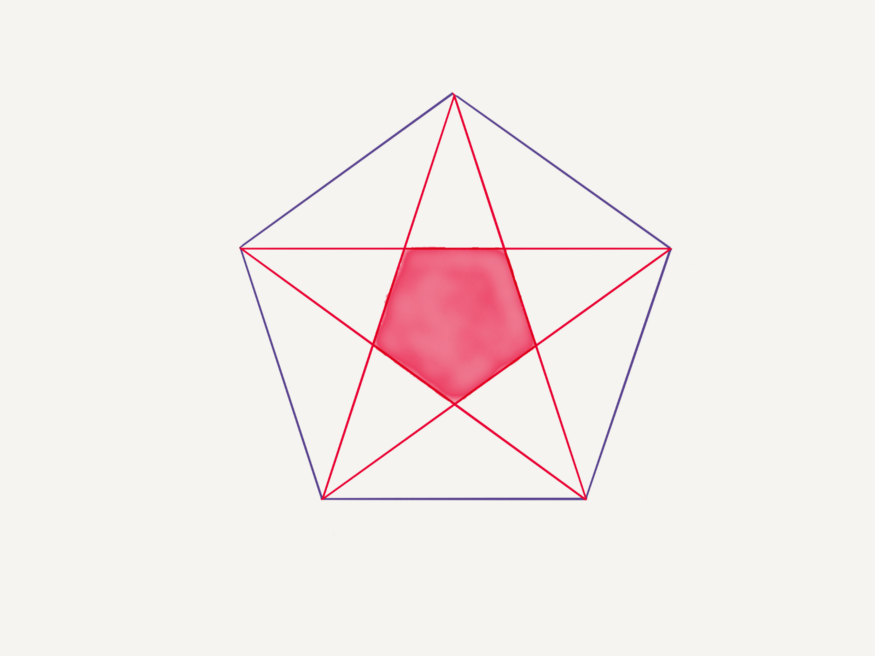
Исключительный пятиугольник
Мы решили сложный вопрос без математики. Когда не знаем о золотом сечении, приходится справляться с кучей линий, квадратными уравнениями и подобным.
Удивительное качество φ
А также отметим ещё одно отличительное свойство φ. Вернитесь и вспомните квадратное уравнение φ.
φ – единственное число, квадрат которого равен сумме самого себя и 1. Нет такого действительного числа, чтобы при добавлении к нему 1 вы увидели квадрат этого числа. И что любопытно, получаем такое:
Вот примечательные постоянные числа. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,… Они не случайные, а происходят из ряда Фибоначчи, где каждый член – сумма двух предыдущих.
Связь между последовательностью Фибоначчи и золотой пропорцией беспрецедентна. Отношение двух идущих друг за другом чисел из ряда приобретает золотое сечение через некоторое время. Вы получите эту пропорцию из каждой цифры, когда возьмёте большое число из последовательности.
Продолжайте вычислять и получите новое число с φ.
Данная информация полезна, потому что помогает легко найти sin 18 или cos 36 без калькулятора. Это тоже упражнение для вас!
Что можно что нельзя объяснить числами
1. В чем состоит проблема многого и единого?
2. «Все состоит из материальных субстанций». Какие достоинства и какие недостатки вы видите в этом суждении?
3. Что можно и что нельзя объяснить числами? Рассмотрите соответствующие примеры.
4. Догонит ли быстроногий Ахилл черепаху? Пока Ахилл добежит до черепахи, она успеет отодвинуться от первоначального места и так бесконечное число раз.
5. Рассказывают такую легенду. Диоген объяснял своему ученику, почему элеаты не соглашались признать факт движения. Дело было на берегу моря, ученик сидел на песке, а учитель расхаживал перед ним. Вдруг ученик захлопал в ладоши. Он сказал Диогену, что видит его движение, что движение, в данном случае Диогена, очевидно, глаза не могут обмануть. Диоген побил ученика палкой. За что?
6. Атомизм принято считать концепцией физики. Объясните, почему атомизм является философской концепцией.
Высокий интеллектуализм Сократа, Платона, Аристотеля
7. Почему Сократ не удовлетворился натурфилософией?
8. На какой вопрос трудно ответить в рамках этики Сократа?
9. Опишите три этапа диалектики Сократа.
10. Как объяснял Сократ свою приверженность философии ненасилия?
11. Как можно прийти к идее «студент»?
12. Что активно по Платону — идея, материя или демург?
13. Видите ли вы какие-либо изъяны в концепции любви Платона?
14. Почему по Аристотелю в единстве материи и формы именно форма играет ведущую роль?
15. Какие добродетели вы цените выше всего?
16. Александр Македонский учился у Аристотеля. Учеником какого философа античности хотели бы быть вы? Почему?
Философия раннего эллинизма
17. За что греки были благодарны киникам?
18. Как вы относитесь к цинизму?
19. Какая связь существует между физикой и этикой эпикуреизма?
20. Какая связь существует между физикой и логикой стоиков?
21. Какая связь существует между логикой и этикой скептицизма?
22. Имея в виду кинизм, эпикуреизм, стоицизм и скептицизм, дайте характеристику своим знакомым и себе самому.
23. Что является, согласно Плотину, сущностью всего мироздания, в том числе человека и общества?
24. Как вы относитесь к мистике? Дайте обоснование своей точке зрения.
2. Средневековая философия
Философские идеи в средние века чаще всего были облачены в религиозные одежды. Строго говоря, религия не является философией. Религия — это богопослушание, сверхъестественная связь человека с богом. Для религии характерны чудеса, безудержная вера в догматы. В философии то и другое ставится под сомнение. В то же время нельзя не видеть и определенное сходство религии и философии. Как мы видели на примере анализа воззрений Платона и Аристотеля, тема бога не является чуждой для философии. Поиски единого очень часто приводят к теме бога. В религиозных воззрениях, равно как и в любых других воззрениях, всегда содержатся философские идеи. Именно с этих позиций рассмотрим христианство. Нас интересуют новые философские принципы, развитые в средние века.
Средневековая философия выдвинула плеяду выдающихся философов: Августин, Ансельм, Абеляр, Фома Аквинский. Но даже на этом фоне выделяется величественная фигура Иисуса Христа. Многие считают его великим философом. Величие это видят в том, что он выдвинул философию не для избранных мудрецов, а для всех, образно говоря, даже для нищих духом, например для детей.
Греческое слово «Библиа» означает «книги», они составляют Ветхий и Новый Заветы. Завет — это договор Бога с родом человеческим. В случае, если речь идет о божественной личности, слово бог пишется с большой буквы — Бог. Для удобства читателя мы пронумеруем основные библейские идеи философской значимости.
1. Монотеизм. Бог един и уникален (монос по-гречески означает одно, единое). Античному признанию существования многих богов, т. е. политеизму, приходит конец. Не только христианство, но и иудаизм и ислам настаивают на единобожии. Каков же философский смысл монотеизма? Надо полагать, отнюдь не случайно философия приобретает монотеистический вид. В чем состоят жизненные корни монотеизма? Прежде всего в усилении субъективного, человеческого начала. Платон и Аристотель называли божественными космос, звезды, т. е. неличностное. В библии божественным является только сам Бог. Монотеизм — это результат более глубокого, чем в античности, понимания субъективного.
2. Теоцентризм (центральное положение Бога, на греческий слово «бог» переводится как теос). В соответствии с принципами теоцентризма источником всякого бытия, блага и красоты являлся Бог. Античная философия была космоцентрична, а не теоцентрична. Теоцентризм по сравнению с космоцентризмом опять же усиливает личностное начало.
3. Креационизм (латинское созидание). Креационизм — учение о сотворении мира Богом из ничто. В философии не считают, что из ничто можно сделать нечто. В креационизме философы ценят развитие идеи творения, творчества. Демург Платона — мастеровой, но не творец. Бог Аристотеля также не творит, он лишь созерцает сам себя. Креационизм содержит в себе идею творчества. Этой философской идее всегда обеспечивается яркая жизнь.
4. Вера. Библия возвышает веру над интеллектом, в то время как в античности разум сводился к интеллекту, который считался враждебным вере. Вера — слово итальянских корней и буквально означает «то, что обеспечивает истину». Веры бывают разные, в том числе и несостоятельные. Для нас важны сейчас не различия в вере, а сам факт их наличия, необходимость их философского осмысления. Каждый человек верит, он что-то считает истинным. Вера — это личностное самоопределение человека, составная часть его внутреннего мира. Именно средневековая философия впервые разработала проблематику веры.
5. Добрая воля. Только тот человек соблюдает библейские заветы, который обладает доброй волей, кто способен за счет собственных усилий исполнить то, чего хочет Бог. Греки считали, вспомним Сократа, что добро совершается посредством интеллекта и только. Христианство открыло горизонт воли.
6. Этика долга, морального закона. Греки считали, что моральный закон — это закон самой природы, который и на стороне бога и человека выступает как добродетель. Христиане считают, что моральный закон дает Бог, человек ответственен перед Богом. Христианская этика — это по преимуществу этика долга перед Богом.
7. Совесть. Нравственность самого человека есть прежде всего совесть. Совесть — это познание, сопровождающее связь человека с Богом, это со-весть. В Ветхом Завете слово совесть не встречается, а в Новом Завете оно используется около 30 раз. Ветхий Завет создавался до нашей эры, а Новый Завет — после. Мы приводим этот факт, ибо он показывает, что совесть — это новое изобретение. Благодаря совести человек открывает свою греховность, а значит, и пути ее преодоления.