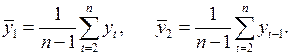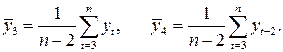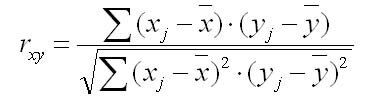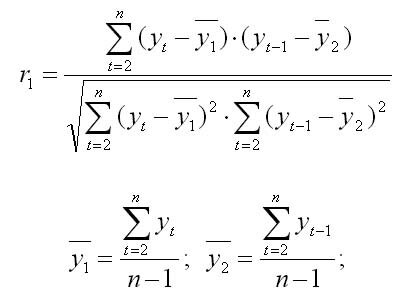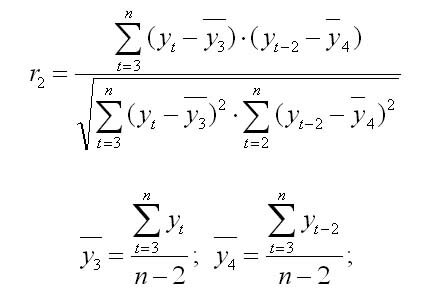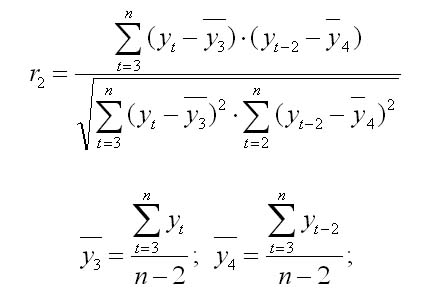Что измеряет коэффициент автокорреляции
Автокорреляция, коэффициент автокорреляции



При обработке временных рядов необходимо учитывать наличие автокорреляции и авторегрессии, при которых значения последующего уровня ряда зависят от предыдущих значений.
Автокорреляция – явление взаимосвязи между рядами: первоначальным и этим же рядом сдвинутым относительно первоначального положения на h моментов времени.
Авторегрессия – регрессия, учитывающая влияние предыдущих уровней ряда на последующие ряды.
Количественно автокорреляцию можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Формула для расчета коэффициента автокорреляции имеет вид:
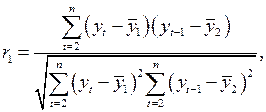
Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда 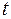
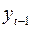
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями 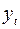
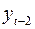
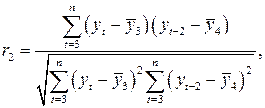
Сдвиг между соседними уровнями или сдвинутыми на любое число периодов времени называют временным лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше 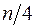
Свойства коэффициента автокорреляции.
1. Коэффициент корреляции строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т.е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка 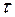
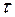
Пусть имеются некоторые условные данные (таблица 11) об общем количестве поступившей товарной продукции на склад предприятия.
Таблица 11 – Общее количество поступившей товарной продукции на склад.
| Год | Квартал | 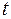 | Количество поступившей товарной продукции, 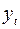 |
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV |
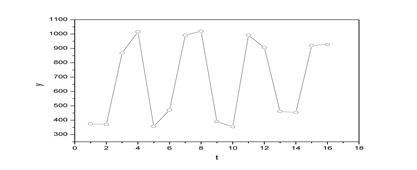
Построим поле корреляции (рисунок 4).
Рисунок 4 – Поле корреляции
Из графика видно, что значения 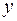
Таблица 12 – Первая вспомогательная таблица.
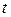 | 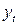 | 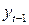 | 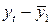 | 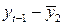 | 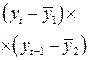 | 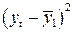 | 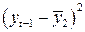 |
| – | – | – | – | – | – | ||
| -328,33 | -288,13 | 94601,72 | 107800,59 | 83018,90 | |||
| 169,67 | -292,13 | -49565,70 | 28787,91 | 85339,94 | |||
| 315,67 | 205,87 | 64986,98 | 99647,55 | 42382,46 | |||
| -342,33 | 351,87 | -120455,66 | 117189,83 | 123812,50 | |||
| -228,33 | -306,13 | 69898,66 | 52134,59 | 93715,58 | |||
| 292,67 | -192,13 | -56230,69 | 85655,73 | 36913,94 | |||
| 320,67 | 328,87 | 105458,74 | 102829,25 | 108155,48 | |||
| -309,33 | 356,87 | -110390,60 | 95685,05 | 127356,20 | |||
| -344,33 | -273,13 | 94046,85 | 118563,15 | 74600,00 | |||
| 292,67 | -308,13 | -90180,41 | 85655,73 | 94944,10 | |||
| 205,67 | 328,87 | 67638,69 | 42300,15 | 108155,48 | |||
| -238,33 | 241,87 | -57644,88 | 56801,19 | 58501,10 | |||
| -245,33 | -202,13 | 49588,55 | 60186,81 | 40856,54 | |||
| 220,67 | -209,13 | -46148,72 | 48695,25 | 43735,36 | |||
| 227,67 | 256,87 | 58481,59 | 51833,63 | 65982,20 | |||
| Сумма | 9,05 | 0,05 | 74085,16 | 1153766,39 | 1187469,73 | ||
| Среднее значение | 699,33 | 663,13 | – | – | – | – | – |
Вычисляем коэффициент автокорреляции первого порядка
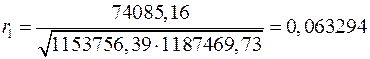
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка (таблица 13).
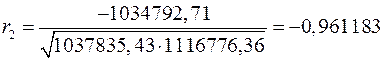
Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу (таблица 14).
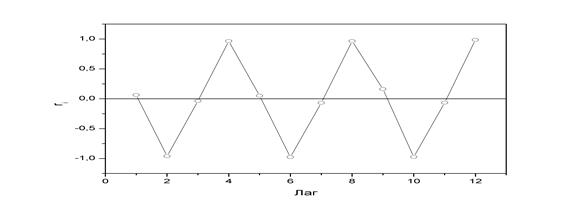
Анализ коррелограммы (рисунок 5) и графика исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
Рисунок 5 – Коррелограмма
Таблица 13 – Вспомогательная таблица.
| Лаг | Коэффициент автокорреляции уровней |
| 0,063294 | |
| –0,961183 | |
| –0,036290 | |
| 0,964735 | |
| 0,050594 | |
| –0,976516 | |
| –0,069444 | |
| 0,964629 | |
| 0,162064 | |
| -0,972918 | |
| -0,065323 | |
| 0,985761 |
Таблица 14 – Сводная таблица расчетных показателей.
Автокорреляция (Autocorrelation)
Автокорреляция (последовательная корреляция) – сила взаимосвязи Наблюдений (Observation) во Временном ряду (Time Series). Коррелограммы – графики автокорреляции и частичной автокорреляции, широко используются при анализе и прогнозировании временных рядов.
Пример. Используем Датасет (Dataset) минимальных суточных температур за 10 лет (1981–1990) в г. Мельбурн, Австралия. Единицы измерения – градусы Цельсия, всего 3650 наблюдений. Для начала импортируем необходимые библиотеки:
Получим токен Google Cloud SDK, чтобы использовать Google-таблицу:
Загрузим набор данных:
Визуализируем данные, чтобы увидеть сезонные колебания:

Температуры в данном случае – серия Pandas, и создается линейный график временного ряда.
Корреляция и автокорреляция
Статистическая корреляция отображает силу взаимосвязи между двумя переменными.
Мы можем предположить, что распределение каждой переменной соответствует распределению Гаусса (кривая колокола). В этом случае мы можем использовать Коэффициент корреляции Пирсона (Pearson Correlation Coefficient), чтобы суммировать корреляцию между переменными.
Мы можем вычислить корреляцию для наблюдений временного ряда, используя n-ное и (n-1)-е наблюдения. Последние еще называют лагами. Поскольку корреляция наблюдений временного ряда вычисляется со значениями того же ряда в предыдущие моменты времени, это еще называется последовательной корреляцией.
График автокорреляции временного ряда (AutoCorrelation Function – ACF) иногда называют коррелограммой. Давайте построим такой с помощью функции plot_acf() библиотеки statsmodels:

При исполнении кода ячейки создается двухмерный график, демонстрирующий корреляцию между двумя временными рядами – исходным и сдвинутым на один день назад. Мы ограничили количество значений по оси x до 35, чтобы улучшить читаемость графика.
Поскольку температурная разница между 1 и 2-м июля, очевидно, небольшая, то и корреляция будет стремиться к единице (второй столбец графика слева). Но когда мы исследуем разницу температур между 1 июля и 4 августа (35 дней разницы – крайний столбец слева), коэффициент корреляции очевидно будет меньше.
Если вы хотите ознакомиться с пошаговой последовательностью построения графика автокорреляции, посмотрите обучающее видео от Brandon Rohrer.

Доверительные интервалы изображены в виде полупрозрачного голубого конуса. По умолчанию установлен доверительный интервал 95%. Если голубая точка каждого из 35 коэффициентов лежит за пределами этой фигуры, то является статистически значимой единицей.
Частичная автокорреляция
Частичная автокорреляция (Partial Autocorrelation – PACF) – это сводка отношений между наблюдением во временном ряду с наблюдениями на предыдущих временных шагах с удаленными взаимосвязями промежуточных наблюдений. Частичная автокорреляция при лаге k возникает после устранения влияния любых корреляций с более короткими лагами.
Автокорреляция для наблюдения и наблюдения на предыдущем временном шаге состоит как из прямой корреляции, так и из косвенной корреляции. Эти косвенные корреляции являются линейной функцией корреляция наблюдения с наблюдениями на промежуточных временных шагах.
Именно эти косвенные корреляции пытается устранить функция частичной автокорреляции. Построим такой график для нашего температурного датасета:
При выполнении примера создается двухмерный график частичной автокорреляции для первых 50 лагов:

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автокорреляция, Коэффициент автокорреляции
При наличии во временном ряде тренда и сезонных колебаний значения любого последующего уровня ряда зависят от предыдущих. Корреляционная зависимость между последовательными уровнями временного ряда в эконометрике называется автокорреляцией уровней рада.
Количественно ее можно найти с помощью коэффициента корреляции между уровнями начального временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов по времени.
Определим коэффициент корреляции между рядами уt и yt-1.
Формула для расчета коэффициента корреляции можно представить в виде:
Коэффициент автокорреляции
В качестве переменной X рассматривают ряд у2, у3, …, у6 в качестве переменной у — ряд у1, у2, …, у5. Тогда приведенная формула для расчета коэффициента корреляции примет вид
Эта величина — коэффициент автокорреляции первого порядка, так как он определяет зависимость между соседними уровнями ряда t и t-1
Аналогично определяют коэффициенты автокорреляции второго и более высоких порядков.
Число периодов, по которым определяется коэффициент автокорреляции, называют лаг автокорреляции. С ростом лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается что лаг должен определяться отношением n/4 — количество наблюдений деленных на 4.
Свойства коэффициента автокорреляции
По коэффициенту автокорреляции судят о наличии линейной тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (степенную функцию или экспоненту), коэффициент автокорреляции может быть меньше 0,7.
По знаку коэффициента автокорреляции нельзя делать судить о возрастающем или убывающем направлении связи в ряду.
Коррелограмма
Последовательность коэффициентов автокорреляции уровней первого, второго и других порядков называется автокорреляционной функцией временного ряда. График значений коэффициентов автокорреляции разных порядков называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет найти лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями временного ряда наиболее тесная.
Анализ коэффициентов автокорреляции
Если максимальным оказался коэффициент автокорреляции первого порядка, временной ряд содержит только тенденцию (тренд).
Если максимальным оказался коэффициент автокорреляции порядка n, ряд содержит циклические колебания с периодичностью в n моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым (близок к 0), можно сказать, что либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит нелинейную тенденцию, для выявления которой проводят дополнительный анализ.
Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
Для перехода на страницу выполнения контрольных по эконометрике жмите сюда
Корреляционная зависимость между уровнями взаимосвязанных рядов динамики
При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней 2-х или более рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования:
Коэффициент вычисляется по непосредственным данным рядов динамики, когда фактические уровни одного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период, принимаются в качестве результативного признака (этот сдвиг называется лагом). Коэффициент рассчитывается на основе формулы коэффициента корреляции для парной зависимости:
Примечание: во избежание путаницы, следует обратить внимание на порядок, по которому будет производиться сдвиг уровней, а именно, вниз или вверх. Соответственно и в формулах по разным источникам, ряд со сдвигом отображают либо так y t-1 либо y t+1
Формула для расчета коэффициента уровней ряда 1-го порядка:
Формула для расчета коэффициента уровней ряда 2-го порядка:
Для суждения о наличии или отсутствии в исследуемом ряду, фактическое значение коэффициента сопоставляют с табличным для 5% или 1% уровня значимости (т. е. по величине вероятности допустить ошибку при принятии гипотезы о независимости уровней ряда). Если расчетное значение меньше табличного, то гипотеза об отсутствии принимается и, наоборот, в противном случае, отвергается.
Последовательность коэффициентов 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов от величины лага (порядка коэффициента ) называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты. Так, если наиболее высоким оказался коэффициент первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени. Если же ни один из коэффициентов не является значимым, то можно сделать одно из двух предположений:
Необходимо подчеркнуть, что линейные коэффициенты характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому, по коэффициентам можно судить только о наличии или отсутствии линейной зависимости (или близкой к линейной). Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент уровней исходного ряда может приближаться к нулю. По знаку коэффициента нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную уровней, однако, при этом могут иметь убывающую тенденцию.
Для проверки ряда на наличие нелинейной тенденции рекомендуется вычислить линейные коэффициенты для временного ряда, состоящего из логарифмов исходных уровней. Отличные от нуля значения коэффициентов будут свидетельствовать о наличии нелинейной тенденции.
Пример расчета:
Коэффициент 1 порядка
Расчет коэффициента 1-го порядка
Коэффициент автокорреляции. Их свойства



Аналогично определяют коэффициенты автокорреляции второго и более высоких порядков.
В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом:
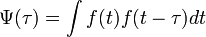
и показывает связь сигнала (функции ) с копией самого себя, смещённого на величину τ.
Свойства коэффициента автокорреляции
По коэффициенту автокорреляции судят о наличии линейной тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (степенную функцию или экспоненту), коэффициент автокорреляции может быть меньше 0,7.
По знаку коэффициента автокорреляции нельзя делать судить о возрастающем или убывающем направлении связи в ряду.
Коррелограмма
Последовательность коэффициентов автокорреляции уровней первого, второго и других порядков называется автокорреляционной функцией временного ряда. График значений коэффициентов автокорреляции разных порядков называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет найти лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями временного ряда наиболее тесная.
Анализ коэффициентов автокорреляции
Если максимальным оказался коэффициент автокорреляции первого порядка, временной ряд содержит только тенденцию (тренд).
Если максимальным оказался коэффициент автокорреляции порядка n, ряд содержит циклические колебания с периодичностью в n моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым (близок к 0), можно сказать, что либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит нелинейную тенденцию, для выявления которой проводят дополнительный анализ.