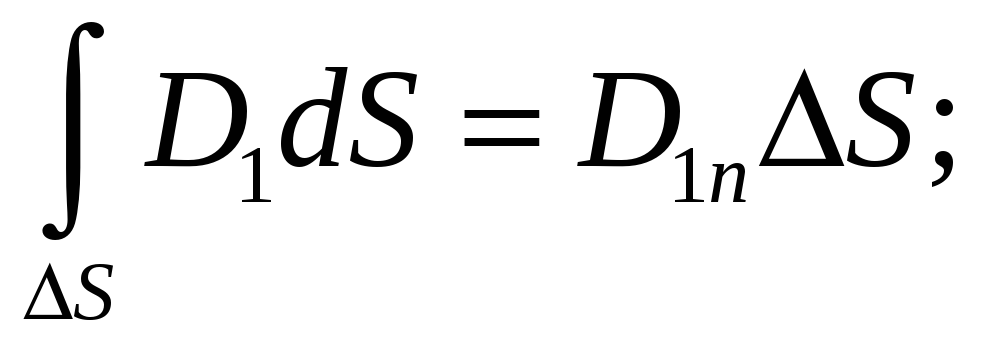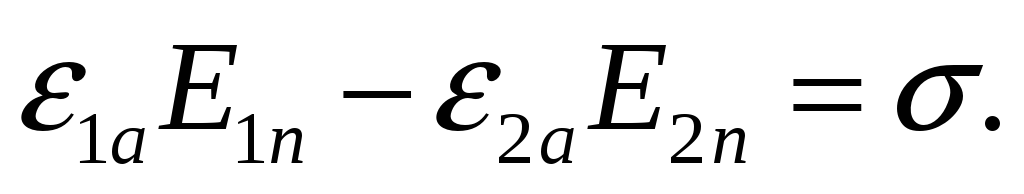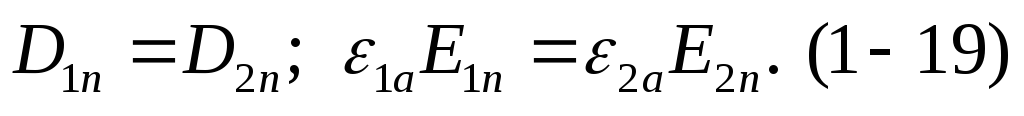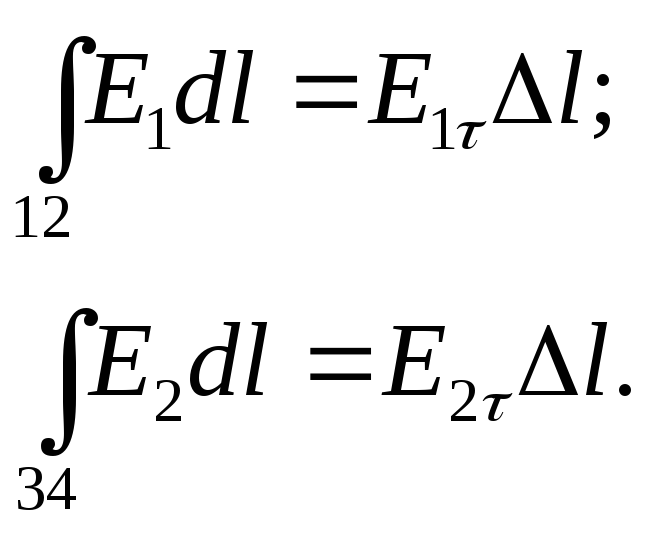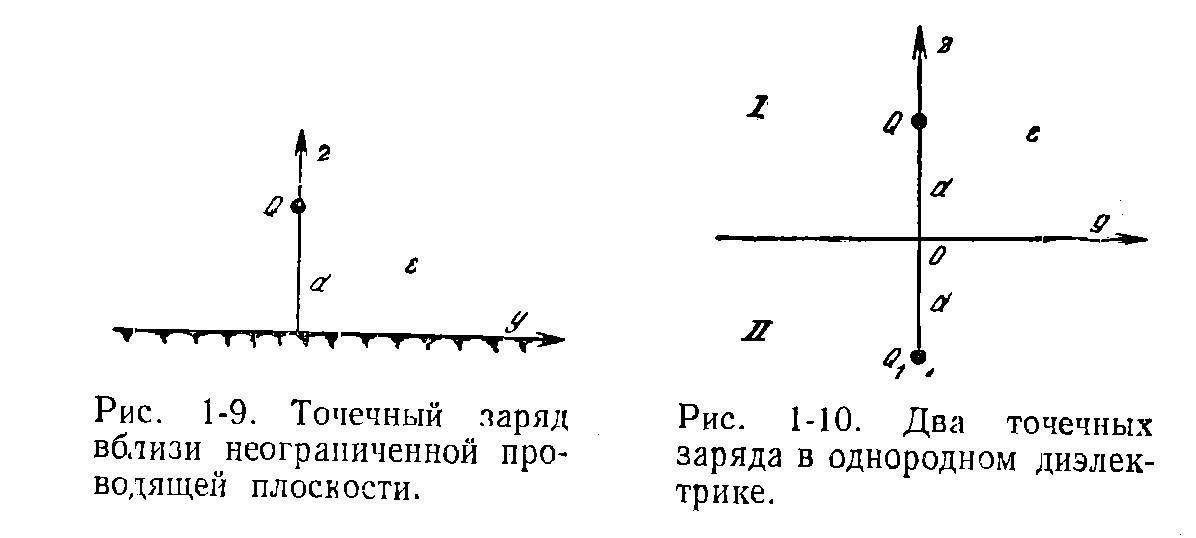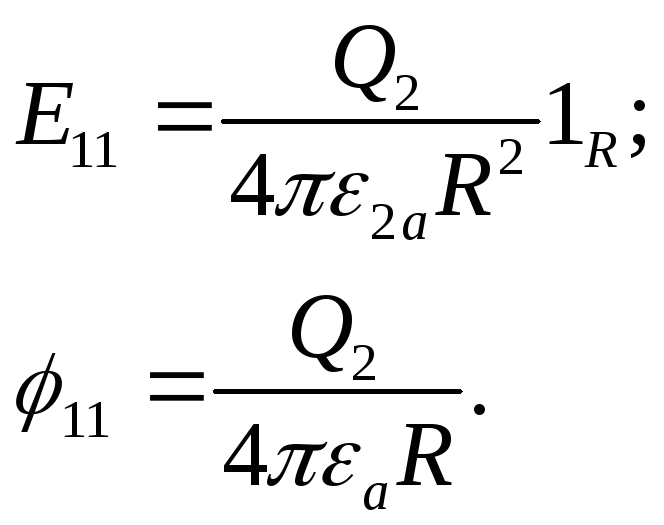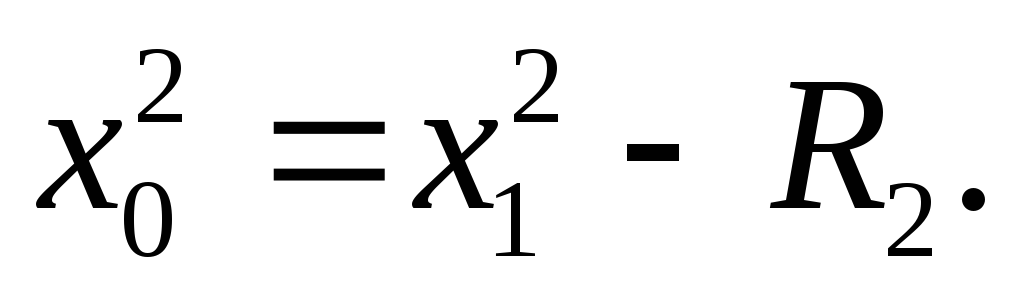граничные условия в электростатическом поле

Граничные: условия в электростатическом поле

На границе двух различных сред векторы поля должны удовлетворять определенным условиям, которые называются граничными.

Представим поток вектора D в виде суммы трех потоков:

Если площадка ∆S невелика, то можно считать, что во всех точках этой площадки вектор D имеет одну и ту же величину, тогда

Если высоту цилиндра уменьшать так, чтобы площадки ΔS стремились к границе между диэлектриками, то поток через боковую поверхность будет стремиться к нулю. В пределе он обратится в нуль, и тогда Dln∆S—D2n∆S = σ∆S. После сокращения на ∆S мы получим первое граничное условие:

Нормальная составляющая вектора электрической индукции на границе двух непроводящих сред претерпевает скачок, равный поверхностной плотности свободных зарядов, распределенных на границе.

Нормальная составляющая вектора D на границе непрерывна.

Для получения второго граничного условия проведем замкнутую линию L так, чтобы одна ее часть находилась в первом диэлектрике, другая — во втором. Зададимся направлением обхода по часовой стрелке и составим циркуляцию вектора напряженности по контуру 1-2-3-4. В электростатическом иоле циркуляция вектора Е равна нулю.

Представим циркуляцию в виде четырех линейных интегралов:

Если длина отрезка ∆1 невелика, то вектор Е можно считать одинаковым на всем отрезке. Тогда

Если отрезки 2-3 и 4-1 постепенно уменьшать так, чтобы в пределе они стали равными 1улю, а отрезки ∆1 совпали с граничной поверхностью, то остальные два интеграла обратятся в нуль и E1τ∆l — E2τ∆l = 0. После сокращения на ∆1 получим второе граничное условие:

На границе двух непроводящих сред касательные составляющие вектора напряженности электрического поля равны. Надо отметить, что на поверхности раздела двух сред потенциал непрерывен φ1=φ

Если одна из сред проводящая, то граничные условия несколько изменятся. В проводящей среде векторы поля равны нулю, а потенциал всех точек проводника, один и тот же. Пусть первая среда диэлектрик с проницаемостью ε, вторая — проводник; тогда граничные условия запишутся следующим образом;

Метод зеркальных изображений

Если электрические заряды расположены вблизи границы двух или нескольких разнородных сред, то векторы поля можно определить, применив искусственный метод расчета, который носит название метода зеркальных изображений. Идея метода заключается в том, что вместо неоднородной среды рассматриваются среды однородные, влияние же неоднородности учитывается введением фиктивных зарядов. Определив векторы поля от совместного действия этих зарядов, записывают граничные условия основной задачи и, пользуясь ими, находят величину введенных фиктивных зарядов и искомые векторы поля.

Граничным условием для рассматриваемой задачи является равенство нулю касательной составляющей напряженности электростатического поля на проводящей поверхности. Покажем, что поле двух зарядов, заданного Q и фиктивного Q1, равноудаленных от граничной поверхности, т. е. отстоящих друг от друга на расстоянии 2d, и расположенных в однородном диэлектрике с проницаемостью ε, такое же, как и исследуемое поле. Величина заряда Q1 определится из граничного условия. В области 1 заряд и среда такие же, как и в основной задаче. При одинаковых граничных условиях, по теореме единственности решения уравнений поля, векторы поля в обеих задачах должны быть одинаковыми. На плоскости хОу напряженность поля двух точечных зарядов по

По условию касательная составляющая Eгр равняется нулю, т. е.

Следовательно, Q1 = — Q. Фиктивный заряд должен быть равен заданному по величине и иметь противоположный знак.

В любой точке пространства над плоскостью хОу, т. е. в объеме, занятом полем,

Плотность поверхностных зарядов, индуцированных на граничной плоскости

Можно показать, что весь заряд, индуцированный на граничной поверхности проводящей среды, равен фиктивному заряду. Для этого надо произведение σ_индdS проинтегрировать по всей плоскости хОу.

Следует заметить, что заряд Q притягивается к проводящей плоскости с силой

В области под плоскостью хОу поля нет, так как среда, заполняющая эту область, проводящая.

Пример 2. Заряд Q расположен вблизи плоскости раздела двух диэлектриков и отстоит от нее на расстоянии d. Проницаемость диэлектрика, в которой находится заданный заряд, равна ε1. Проницаемость второго диэлектрика ε2. Требуется определить напряженность электростатического поля и потенциал в обоих диэлектриках. На плоскости раздела должны иметь место следующие соотношения: Е1τ = E2τ; ε1E1n=ε2Е2n. Второе соотношение справедливо в том случае, когда на поверхности раздела двух диэлектриков нет свободных зарядов. Решение рассматриваемой задачи можно свести к решению двух более простых задач. Рассмотрим первую из них.

В однородном диэлектрике с проницаемостью ε1 на расстоянии 2d друг от друга расположены два точечных заряда Q и Q1. Заряды равноудалены от плоскости хОу.. Среда одинаковая, заряд один и тот же. Следовательно, если для произвольной точки, лежащей на плоскости хОу, в обеих задачах вектор Е будет одинаковым, то и в любой точке области 1 на основании теоремы единственности решение уравнений поля должно быть одинаковым. Напряженность и потенциал ноля двух точечных зарядов можно определить методом наложения:

Эти же формулы будут справедливы для основной задачи в области I, если будут выполнены граничные условия. На плоскости xOy:

По условиюЕ1τ = Eτ; E1n=Еn. Рассмотрим вторую, простую задачу. В однородном диэлектрике с проницае­мостью ε2 находится точечный заряд Q2. Он отстоит на расстоянии d от плоскости хОу. на­ходим, что для области II под плоскостью хОу условия обеих задач совпадают. Диэлектрик один и тот же; зарядов нет. Если на плоскости хОу значение вектора Е в обеих задачах будет одинаковым, то по тео­реме единственности Е в любой точке области II определится как на­пряженность поля точечного заряда Q2.

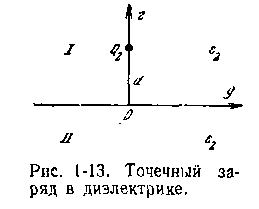
Для точечного заряда

Пользуясь этим выражением можно определить неизвестные фиктивные заряды

Знаки зарядов Q и Q2 всегда одинаковые. Знаки зарядов Q1 и Q одинаковые при ε1>ε2 и разные при ε1 1, т. е. для полу­пространства с положительно заряженной осью. В первом случае ок­ружности расположены справа от оси xОу, во втором случае — слева. Величины х0, x1 и R связаны соотношением

в чем можно убедиться, подставив значения х1 и R. Можно показать, что линии вектора Е представляют собой семейство окружностей

которые проходят через заряженные оси. Радиус их равен , а координаты центров х = 0 и y=y1.

Источник

Граничные условия в электростатическом поле

1.1. Основные уравнения

Для электростатических полей, обусловленных действием неподвижных электрических зарядов, справедливы уравнения:

или (1.1)

Вектора напряженности электрического поля и электрической индукции для большинства задач определены линейным соотношением:

В однородной среде ( e = const ) для потенциала справедливо уравнение Пуассона –

(1.4)

и, в частности, где отсутствуют свободные заряды, уравнение Лапласа –

Граничные условия

Граничные условия определяют поведение векторов поля (нормальных и тангенциальных составляющих) на границе раздела двух сред, параметры которых меняются скачком. Для всех электрических полей имеют место основные граничные условия, которые являются прямым следствием системы уравнений Максвелла:

или (1.6)

Граничные условия для диэлектриков

На границе раздела двух диэлектриков свободный поверхностный заряд s = 0. Следовательно,

Граничные условия на поверхности раздела диэлектрик – проводник

и

Условие (1.11) с учетом (1.3) принимает вид

(1.12)

и его называют граничным условием Неймана, записанным в дифференциальной форме. То же граничное условие в интегральной форме

где под q понимают суммарный заряд электрода.

Поверхность электрода является эквипотенциальной поверхностью, что записывают в виде

(1.14)

и называют граничным условием Дирихле.

1.2. Прямая задача электростатики

Во многих случаях приходится решать сложные задачи, из которых наиболее типичными являются следующие:

1. Нахождение поля при неизвестном местоположении исходных зарядов, но заданном электрическом потенциале на границах области. В инженерной практике потенциалы электродов обычно задаются источниками питания и могут быть измерены или вычислены.

2. Нахождение потенциала электрического поля, создаваемого заданным распределением объёмных электрических зарядов в пространстве.

Прямой метод вычисления потенциала электрического поля в этих задачах состоит в решении уравнения Пуассона (1.4), которое в декартовой системе координат принимает вид

(1.15)

или уравнения Лапласа (1.5):

Уравнения (1.15), (1.16) относятся к классу дифференциальных уравнений в частных производных эллиптического типа. Эти уравнения в зависимости от симметрии задачи могут быть записаны в цилиндрических или сферических координатах.

Для получения единственного решения уравнения (1.15) или (1.16) необходимо дополнить их граничными условиями. Различают три типа граничных условий:

1. Граничное условие Дирихле : значение j задано на некоторой замкнутой области. Обычно это проводящая поверхность или поверхность электрода, потенциал которой постоянен (см. 1.14).

3. Смешанная краевая задача (на границе задается линейная комбинация потенциала j и его нормальной производной).

Целью расчёта является нахождение потенциала j и напряженности поля по заданному расположению и форме заряженных тел – электродов – и граничным условиям. Такая задача называется прямой задачей. Если плотность заряда в каждой точке пространства известна, то потенциал как функция положения определяется уравнением Пуассона. Если же требуется найти поле в диэлектрике, содержащем заряженные проводящие тела, то ищут решение уравнения Лапласа, т.е. решают прямую задачу электростатики в постановке Неймана или Дирихле. При этом совокупность всех проводящих тел образуют границу области существования поля. Эта задача имеет единственное решение, если найденная потенциальная функция удовлетворяет уравнению Лапласа и заданным граничным условиям.

1.3. Методы решения электростатических задач

Общие методы решения уравнения Лапласа при заданных граничных условиях на тех или иных поверхностях изучаются в соответствующем разделе математической физики. Ограничимся здесь лишь указанием некоторых приемов, изложенных в учебной электротехнической литературе [1] – [7]. К ним следует отнести:

а) Использование интегральных уравнений для решения симметричных задач;

в) Метод изображений;

д) Метод средних потенциалов;

е) Метод разделения переменных (Фурье).

В настоящем пособии рассматриваются метод наложения совместно с методом зеркальных изображений.

Метод наложения. Формулы Максвелла

В случае линейной среды ( = const ) по методу наложения имеем:

Потенциалы и заряды проводящих тел связаны между собой линейными соотношениями, которые называются формулами Максвелла. Если известны заряды электродов, то их потенциалы могут быть найдены путём решения задачи Неймана. В этом случае связь осуществляется потенциальными коэффициентами a :

(1.17)

Если известны потенциалы электродов, то, решив задачу Дирихле, можно найти заряды электродов и записать формулы Максвелла с емкостными коэффициентами:

(1.18)

где собственный емкостный коэффициент при всех остальных (кроме ), равных нулю, взаимный емкостный коэффициент при всех остальных (кроме ), равных нулю.

Вместо линейных соотношений (1.18) более удобно применять формулы с частичными емкостями, которые связывают заряды электродов и напряжения между ними.

Формулы с частичными емкостями:

(1.19)

Символом обозначают потенциал электрода, значительно удалённого от области исследования поля. Для системы электродов, линейные размеры которых ограничены, за ноль принимается потенциал бесконечно удаленной точки. Если электроды (теоретически) уходят в бесконечность, то в качестве известного нулевого потенциала указывают точку (или линию), расположенную на границе симметрии задачи. Определять потенциал этой точки необходимо, так как только в этом случае однозначно определяются потенциалы остальных точек (электродов).

1.4. Поля электродов простых геометрических форм

Поле шарового заряда

Заряд q на проводящей шаровой поверхности радиуса R в силу симметрии распределяется равномерно, и потенциал вне сферы определяется выражением:

Уравнение r = const будет уравнением эквипотенциальной поверхности, все они образуют концентрически расположенные сферы.

Если с этой сферой совместить проводящую поверхность второго электрода, т.е. металлизировать эквипотенциальную поверхность, то можно найти ёмкость сферического конденсатора:

Вектор напряженности поля направлен радиально и равен

Поле длинной заряженной оси, кругового цилиндра и коаксиальных цилиндров

Соответственно потенциал определится логарифмической функцией:

Эквипотенциальные поверхности – боковые поверхности цилиндров, оси которых совпадают с заряженной осью ( r = const ). Радиусы соседних поверхностей, потенциалы которых отличаются на одну и ту же величину, выбираются в геометрической прогрессии с произвольным знаменателем. Поле между двумя металлизированными цилиндрическими поверхностями совпадает с полем цилиндрического конденсатора и с полем заряженного провода.

(1.24)

Область, заключённая между двумя силовыми линиями, называется силовой трубкой. Поток вектора внутри силовой трубки постоянен и определён частью заряда электрода.

Потенциал и функция потока не могут выбираться произвольно, они связаны между собой дифференциальными соотношениями, которые называют условиями Коши – Римана:

Эти условия для рассматриваемого случая легко проверяются, если в выражениях (1.21) и (1.22) от полярных координат перейти к декартовым по формулам:

Решения (1.23) и (1.24) имеют большое прикладное значение, так как расчет поля системы длинных параллельных проводов, применяемых, например, для передачи энергии или для телефонной связи, сводится практически к сложению полей нескольких пар бесконечно длинных разноимённо заряженных осей.

Поле двух разноимённо заряженных осей

Рис. 1.1. Построение эквипотенциали для двух разноименно заряженных осей

Эквипотенциальные поверхности (линии в плоскости чертежа) представляют собой окружности со смещенными центрами. На рис. 1.1 точка p лежит на эквипотенциальной поверхности.

Функция потока V определяется методом наложения с использованием выражения (1.24):

Рис. 1.2. Построение силовых линий напряженности электрического поля для двух разноименно заряженных осей

Координаты центра окружности связаны с заданным значением J условием:

Эквипотенциальные поверхности и силовые линии поля взаимно перпендикулярны.

Поле параллельных цилиндров с несовпадающими осями

Любую эквипотенциальную поверхность можно совместить с поверхностью электрода, потенциал которого равен потенциалу этой поверхности. При этом внешнее поле, которое существует между электродами, не изменится. Этот приём называют металлизацией эквипотенциальных поверхностей.

Рис. 1.3. Взаимное внутреннее расположение двух несоосных цилиндрических электродов

Рис. 1.4. Взаимное внешнее расположение двух цилиндрических электродов

Для случая, изображенного на рис. 1.3, имеем

;

;

Для случая, изображенного на рис. 1.4,

;

(так как );

Вектор напряженности поля находят по формуле (1.3), которая для плоскопараллельного поля принимает вид:

(1.30)

Для того чтобы воспользоваться формулой (1.30), необходимо выбрать систему координат, совмещенную с осями симметрии задачи. Например, ось x направить горизонтально через электрические оси электродов, а ось y совместить с линией нулевого потенциала, т.е. использовать электрическую симметрию задачи.

Поле и ёмкость системы цилиндр – плоскость

Рис. 1.5. Взаимное расположение заряженного цилиндра и плоскости

(1.31)

Поле и ёмкость двухпроводной линии

Потенциал положительно заряженного провода

потенциал отрицательно заряженного провода

напряжение, ёмкость на единицу длины и заряд на единицу длины

1.5. Метод зеркальных отражений

Для расчета электростатических полей, ограниченных какой-либо проводящей поверхностью правильной формы или в которых есть геометрически правильной формы граница между двумя диэлектриками, широко применяют метод зеркальных отражений. Это искусственный приём расчёта, в котором кроме заданных зарядов вводят ещё дополнительные, значения и местоположение которых выбирают так, чтобы удовлетворить граничным условиям в поле. Территориально заряды помещают там, где находятся зеркальные отражения заданных зарядов.

Если заряд (или ) расположен у границы двух диэлектриков (рис. 1.6 a ), то на поверхности раздела наводятся связанные электрические заряды, которые подчиняются граничному условию (1.10).

Исключить действие этих зарядов с заменой их эквивалентным действием сосредоточенных зарядов можно путём разбиения задачи на две части:

а) Поле в той среде, где задан точечный заряд (рис. 1.6б), определяется зарядом и зарядом

Рис. 1.6. а) заряд вблизи границы двух диэлектрических сред; б) расположение эквивалентных зарядов для расчета поля в 1-й среде; в) то же для 2-й среды

Дополнительные заряды должны находиться на том же расстоянии от границы, что и заданный.

Поле и ёмкость двухпроводной линии с учётом влияния Земли

Рис. 1.7. Взаимное расположение линейных заряженных проводов относительно плоской проводящей поверхности (“земли”)

В результате получатся две пары разноименно заряженных осей и в однородной среде. Потенциал в любой точке верхней полуплоскости находится методом наложения от каждой пары зарядов на основании формулы (1.25):

(1.35)

(1.36)

Множители при зарядах и – потенциаль­ные коэффициенты.

Рис. 1.8. Расчетная модель задачи с двухпроводной линией над Землей по методу зеркальных отражений

В данном случае собственные потен­циальные коэффициенты определяются как

а взаимные потенциальные коэффициенты

Они всегда положительны и имеют размерность м/Ф. Полученные формулы связывают заряды и потенциалы проводов. Если заданы потенциалы проводов, то заряды могут быть найдены из решения системы уравнений (1.35) и (1.36):

1.6. Пример аналитического решения задачи электростатики

1. Рассчитать и построить распределение потенциала вдоль оси y при х = 0;

2. Рассчитать и построить распределение плотности заряда s на поверхности земли;

3. Определить частичные емкости проводов.

Рис. 1.9. Двухпроводная линия передачи с заземленным верхним проводом

Поле заряженных проводов суммируется с полем тучи. Используя метод наложения, получим связь потенциалов и зарядов электродов, по формулам Максвелла для потенциальных коэффициентов:

(1.37)

(1.38)

и в, частности, при :

Рис. 1.10. Расчетная модель задачи двухпроводной линии с заземленным верхним проводом по методу зеркальных отражений

Поверхностная плотность заряда на поверхности “земли” определяется нормальной составляющей напряженности суммарного поля:

(1.39)

где x – в метрах. Откуда видно, что к заряду обусловленному наличием тучи добавляются два слагаемых, учитывающих влияние каждого из заряженных проводов.

Емкостные коэффициенты можно выразить через потенциальные коэффициенты :

Для ввода графиков в пакете MathCAD можно использовать:

— меню Insert опция Graph главного меню пакета (рис. 1.11) с последующим выбором типа графика из выпадающего меню;

Все эти пути приводят к одинаковому результату – в поле рабочего файла появляется шаблон двумерного или трехмерного графика соответствующего типа. Шаблоны графиков имеют маркеры ввода “■”, которые необходимо заполнить (рис. 1.11).

Рис. 1.11. Поле рабочего файла в пакете MathCAD с вкладками панели Math

Построим график изменения потенциала вдоль вертикальной оси y при х = 0 (рис. 1.12).

Рис. 1.12. Пример программирования в MathCAD потенциальной функции и ее графического представления

При построении графиков и не следует забывать о физически обусловленной зависимости поведения этих функций вблизи и внутри электродов, что обычно не учитывается в соответствующих математических выражениях и может привести к неверным результатам. Так если расчетная точка попадает внутрь электрода, то следует определить потенциал этой точки равным заданному потенциалу электрода, а напряженность поля внутри электрода для всех точек приравнять нулю.

Рис. 1.13. Пример программирования в MathCAD функции поверхностного свободного заряда

Отметим, что для изменения параметров выводимого графика и масштабной сетки в MathCAD необходимо щелкнуть левой кнопкой мыши на графике, при этом он выделится синей рамкой, и далее нажать правую кнопку мыши. В возникшем контекстном меню следует выбрать команду “ Format …”, после чего появится окно редактирования параметров выводимого графика (рис. 1.14).

Активация того или иного пункта подраздела осуществляется установкой флага (в виде галочки) левой кнопкой мыши.

Рис. 1.14. Окно редактирования параметров выводимого графика

Для изменения параметров линий выводимых графиков необходимо использовать подраздел Traces окна редактирования параметров графика.

3 D -Графики. Создание графика поверхности и карты линий уровня

Трехмерный график можно построить тремя основными способами:

— по двумерному массиву данных в форме ряда значений;

— формированием массива данных в виде матрицы путем программирования функциональной зависимости ее элемента от аргументов;

Если выражение для исследуемой функции определено, то последний способ находит наибольшее применение. В этом случае производят следующие действия:

а) Определяют функцию двух переменных;

б) Указывают границы расчетной области;

в) Задают сколько точек нужно отложить по координатным осям. Введением дискретных аргументов i и j индексируются точки, где определяются значения функции;

г) Определяют координаты и точек через введённые дискретные переменные;

д) Через операцию присваивания определяют значения двумерного массива – матрицы значений исследуемой функции. MathCad линейно интерполирует значения этой матрицы и формирует требуемый график.

Построим график поверхности потенциальной функции (рис. 1.15 слева).

Рис. 1.15. Пример построения потенциальной двумерной функции и эквипотенциалей в заданном сечении

— дважды щелкнуть на графике левой кнопкой мыши или однократно щелкнуть на графике правой кнопкой мыши и выбрать из контекстного меню команду “ Format …”, появится окно 3- D Plot Format ;

Отметим, что MathCAD предоставляет различные возможности изменить внешний вид графика: изменение масштаба; изменение цвета и форматирование линий; форматирование осей введением сетки.

Рис. 1.16. Пример выбора типа графика в подразделе General окна 3- D Plot Format

Рис. 1.17. Пример назначения оцифровки линий равного уровня в подразделе Special окна 3- D Plot Format

Применение функции CreateMesh для построения линии равного уровня

F – трёхэлементный вектор – функция двух переменных u и v ;

G – скалярная функция двух переменных u и v ;

s 0 – нижнее значение для независимой переменной u ;

s 1 – верхний предел (значение) для независимой переменной u ;

t 0 – нижний предел для независимой переменной v ;

t 1 – верхний предел для переменной v ;

sgrid – целое положительное число точек в интервале изменения переменной u ;

tgrid – целое положительное число точек в интервале изменения переменной v ;

Пример описания векторной функции:

;

Пример описания скалярной функции:

Пример описания трёх функций:

f1(x,y) := x f2(x,y) := y f3(x,y) := sin (x) + cos (y).

Число ячеек в созданной сетке: ( sgrid – 1 ) × ( tgrid – 1).

MathCAD использует внутренние возможности при создании массива значений функции двух переменных.

Пример использования функции CreateMesh приведён в Разделе 2.

Источник