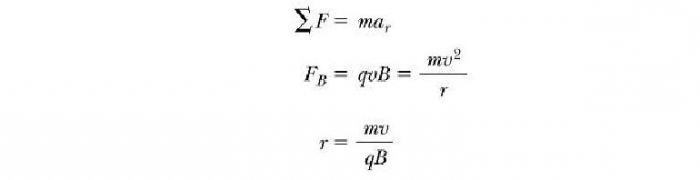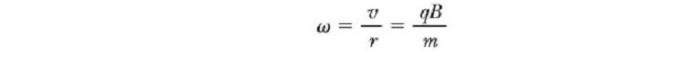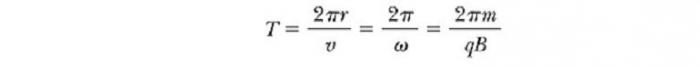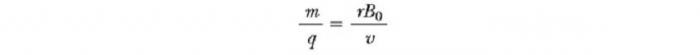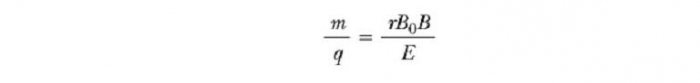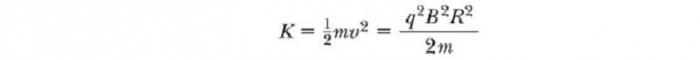движение альфа частицы в магнитном поле

Физика. 10 класс

§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле

Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?

Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).

Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:

где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.

Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.

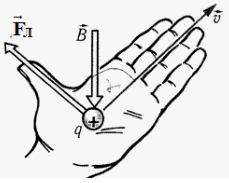
Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.

Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.

* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑

Источник

Сила Лоренца

теория по физике 🧲 магнетизм

Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

Модуль силы Лоренца обозначается как F_Л. Единица измерения — Ньютон (Н).

Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:

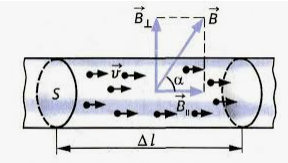
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля → B можно считать неизменным в пределах этого отрезка проводника.

Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:

Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:

Подставляя сюда выражение, полученное для силы тока, получим:

Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:

Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:

α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.

Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45 o к вектору магнитной индукции.

Направление силы Лоренца

Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:

Если левую руку расположить так, чтобы составляющая магнитной индукции → B , перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.

В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.

Работа силы Лоренца

Но так как косинус 90 о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.

Полная сила, действующая на заряд

Следовательно, полная сила, действующая на заряд, равна:

Прямолинейное движение протона возможно в двух случаях:

Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.

Источник

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

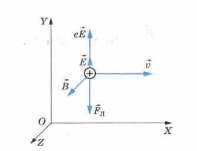
Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

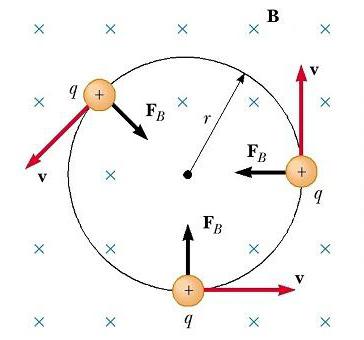
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

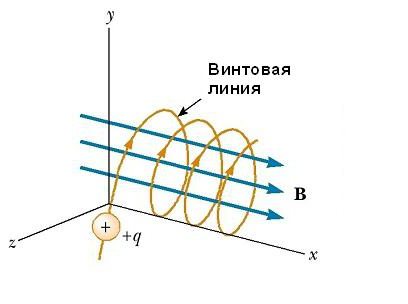
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Неоднородное магнитное поле: как в нем движутся частицы

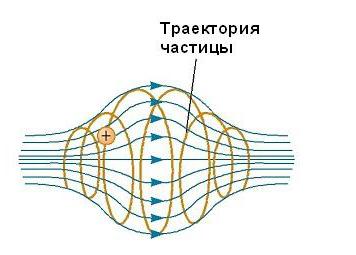
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Как Земля влияет на движение космических частиц

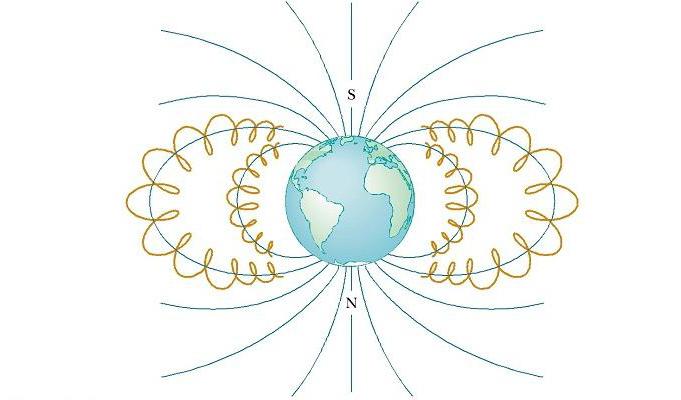
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

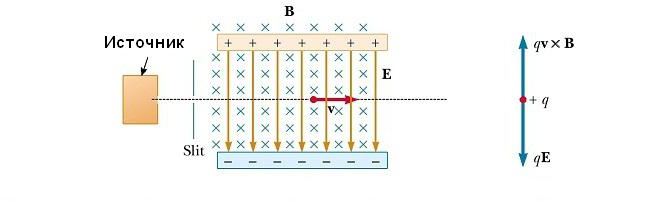
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

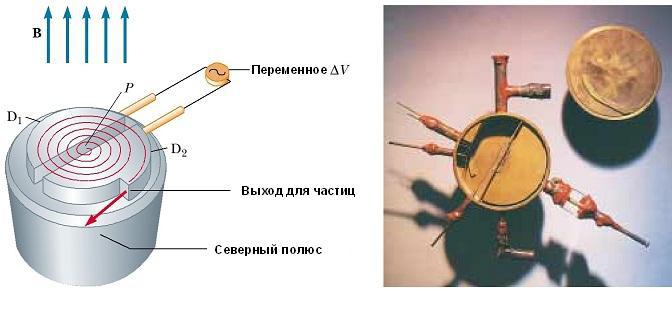
Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Источник

Её главная особенность — для неё не выполняется третье утверждение Ньютона, но справедливо правило сохранения импульса. При этом макроскопическим проявлением перемещения является закон взаимодействия токов.

Общие сведения

Ещё в III—II тысячелетии на острове Магнезия были обнаружены камни, обладающие странными свойствами. Они имели способность притягивать к себе железные предметы. Эти вещества в честь острова получили название магниты. Так как их свойства сохраняются в течение длительного времени, их считают постоянными. Было установлено, что если такой камень разместить на поплавке и положить на него магнит, при его развороте он вернётся в начальное положение. Другими словами, он всегда стремится ориентироваться определённым образом.

Если взять 2 магнита, то, в зависимости от их расположения, они могут притягиваться друг к другу или отталкиваться. Этот эффект объясняется наличием у намагниченных веществ двух полюсов. В 1820 году Христиан Эрстед читал лекцию о тепловом действии тока. Он через проволоку пропускал электричество, демонстрируя, как она разогревается.

Во время эксперимента один из студентов обнаружил, что когда замыкалась цепь, стрелка у рядом находящегося компаса отклонялась. Это вращение и позволило обнаружить связь между электричеством и магнетизмом.

Учёный начал экспериментально изучать эффект. Он предположил, что, так как электрический ток — направленное движение в проводнике заряженных частиц, существует какая-то сила, возникающая вокруг проводящего тела. Обнаружить её можно с помощью компаса. Эту особую пространственную материю назвали магнитным полем. Воображаемые направления, вдоль которых бы расположились стрелки компасов, назвали силовыми линиями.

Опытным путём были установлены характеристики, описывающие движение заряженной частицы в магнитном поле.

К основным из них относят:

Описать магнитную материю можно численно и направлением. За её ориентацию принимается северная сторона, на которую указывает стрелка компаса.

Либо за неё можно принять расположение положительной нормали с током в рамке. Определяют её по правилу буравчика.

Рамка с током

Физиками было установлено, что если взять рамку и пропустить по ней ток, магнитное поле окажет влияние на электроны. В результате происходит их обращение. Вращательное действие силы характеризуется моментом энергии. Именно он и описывает действие материи.

Пусть в магнитном поле расположена прямоугольная рамка. По ней циркулирует ток против часовой стрелки. Вектор индукции направлен вверх. За направление магнитных линий принимается положительная нормаль. По правилу буравчика, если направление поступательного движения винта будет совпадать с направлением тока в проводнике, то вращение винта укажет расположение вектора магнитной индукции поля, создаваемого движением частиц.

Угол между нормалью и вектором обозначают буквой альфа. Естественно, что рамка стремится развернуться так, чтобы быть перпендикулярно полю. Но если она не совпадает с ним по направлению, на неё действует момент силы. Чтобы провести расчёты, необходимо выбрать ось относительно рамки.

Пусть она будет проходить параллельно длинным линиям прямоугольника. Для удобства длина её будет равняться a, а ширина b.

На такую установку будет действовать сила Ампера. Её определение звучит так: модуль вектора равен произведению магнитной индукции на силу тока в проводнике, его длине и синусу угла между направлением поля и заряженными частицами: F = B * I * L * sin (j). Она действует на все стороны рамки. При этом отличается только по направлению.

На рамку оказываются следующие воздействия:

F1 и F2 создают нулевой момент. Они параллельны и направлены в противоположную сторону, образуют пару силы действующих в магнитном поле. Вычисляется она по формуле: M = F * d, где d — расстояние между воздействующими линиями энергии. Таким образом, момент силы в рамке будет определяться так: M = B * a * b * sin (j).

Если принять, что на прямоугольнике намотан провод с числом витков n, а произведение a * b — это площадь, формула примет окончательный вид: M = B * S * n * sin (j).

Сила Лоренца

Магнитное поле действует только на ту частицу, что подвергается воздействию силы Ампера. Пока электрон будет двигаться хаотично, никакого магнитного поля вокруг него не возникнет. Причём эта сила перпендикулярна проводнику и полю.

Получается, что причиной возникновения силы Ампера является какая-то материя, действующая на траекторию заряженных частиц, когда они начинают двигаться в поле.

Пусть в проводнике есть носители зарядов. Их массой в этом случае можно пренебречь. Так как частицами являются отрицательно заряженные электроны, движутся они противоположно направлению тока. На каждый заряд действует сила, которая в сумме даст силу Ампера.

Если взять воображаемое увеличительное стекло и посмотреть, что происходит в середине проводника, возможно было бы увидеть следующее: в окружности тела электрон перемещался бы встречно току и испытывал действие силы, перпендикулярной его движению. Именно она и называется силой Лоренца. Кратко её определение звучит так: равнодействующая всех энергий Ампера, действующих на заряженные частицы, которые перемещаются в поле. Обозначают её Fл.

Кинетическая сила возникает только при движении. Если частица нейтральная (нейтрон), воздействие на неё не оказывается. Чтобы рассчитать эту силу, нужно знать длину проводника и скорость перемещения носителей заряда. Время, которое потребуется электрону, чтобы сменить своё положение, определяют из равенства: t = L / V.

Всю совокупность прошедших частиц можно обозначить Qоб. Это общий заряд, прошедший через радиус проводника за t. Он будет равняться: Qоб = I * t = (I * L) / V.

Учитывая определение, можно утверждать, что Fa = Fл * N. Так как количество частиц, находящихся в проводнике, равняется всему заряду в нём N = Qоб / Q, можно записать: N = I * L / V * Q. Отсюда сила Ампера: Fa = Fл * (I * L) / (V * q). Если сделать подстановку Fа и выразить силу Лоренца, формула для её определения примет вид: Fл = Q * V * B * sin (j), то есть она пропорциональна скорости частицы в магнитном поле, вектору направления индукции и количеству зарядов. Причём сила Лоренца будет наибольшей, когда V перпендикулярно B.

Решение задач

Исследования движения частиц в поле, вызванном магнитной энергией заключается в нахождении сил Лоренца и Ампера за период протекания электрического тока. Существуют определённые типы заданий, с помощью которых можно лучше понять изученный материал и наглядно увидеть, как тесно геометрия переплетается с физикой. Вот некоторые из них:

Часто решение задач требует не только знания нескольких формул, но и понимания, на какую частицу действует магнитное поле и какие силы при этом возникают. Кроме этого, приходится условие изображать схематично на рисунке.

Это часто необходимо для правильного определения направлений действующих сил и упрощения понимания задания. Не стоит забывать, что все вычисления выполняются в системе СИ.

Источник