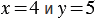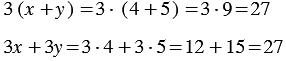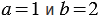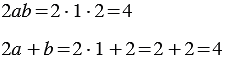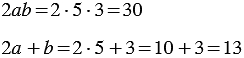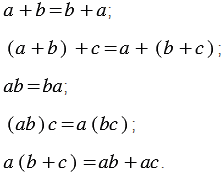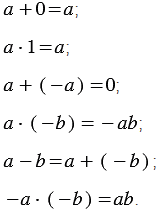Что значит являются ли выражения тождественно равными
Алгебра 7 класс Никольский. 5.9. Тождественное равенство целых выражений. Номер №335
Являются ли следующие выражения тождественно равными (объясните почему):
а) 2 + x и x + 2 ;
б) 2 a + 5 и a − 1 + a + 6 ;
в)
Решение а
2 + x = x + 2 − являются тождественно равными на основании переместительного свойства сложения.
Решение б
2 a + 5 = a − 1 + a + 6 − являются тождественно равными, так как:
a − 1 + a + 6 = (a + a) + ( 6 − 1 ) = 2 a + 5
Решение в
Решение г
2 ( 3 x − 1 ) = 6 x − 2 − являются тождественно равными на основании распределительного свойства сложения.
Решение д
x + y − 2 x + 3 y = 4 y − x − являются тождественно равными, так как:
x + y − 2 x + 3 y = x − 2 x + y + 3 y = 4 y − x
Решение е
2 a − b 3 + 3 b = 2 a − являются тождественно равными, так как:
2 a − b 3 + 3 b = 2 a − 3 b + 3 b = 2 a
Решение ж
3 x + 4 x + 5 x + 1 = 12 x + 1 − являются тождественно равными, так как:
3 x + 4 x + 5 x + 1 = ( 3 + 4 + 5 )x + 1 = 12 x + 1
Решение з
5 x − 2 y + x = − 2 y + 6 x − являются тождественно равными, так как:
5 x − 2 y + x = 5 x + x − 2 y = 6 x − 2 y = − 2 y + 6 x
Решение и
Решение к
3 x(x − y) ≠ 3 y(y − x) − не являются тождественно равными, так как:
Решение л
(x − y)y ≠ (x − y)x − не являются тождественно равными, так как:
Решение м
(x + y)x ≠ (x − y)x − не являются тождественно равными, так как:
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
Найдем их значения при
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных 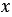
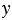

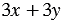
2)
Найдем их значения при
Мы получили один и тот же результат. Однако, можно указать такие значения 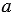
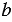
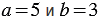
Мы получили разные результаты.
Следовательно, выражения 
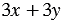
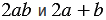
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство 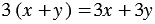
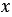
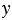
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 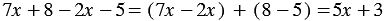
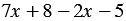
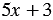
2) 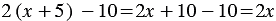
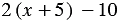
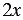
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 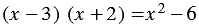
Решение: Приведем контрпример. Если 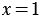
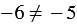
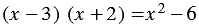
Поделись с друзьями в социальных сетях:
Тождественно равные выражения: определение, примеры.
Получив представление о тождествах, логично перейти к знакомству с тождественно равными выражениями. В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения являются тождественно равными, а какие – нет.
Навигация по странице.
Что такое тождественно равные выражения?
Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроках алгебры в 7 классе. В учебнике по алгебре для 7 классов автора Ю. Н. Макарычев приведена такая формулировка:
Тождественно равные выражения – это выражения, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, которым отвечают одинаковые значения, также называют тождественно равными.
Это определение используется вплоть до 8 класса, оно справедливо для целых выражений, так как они имеют смысл для любых значений входящих в них переменных. А в 8 классе определение тождественно равных выражений уточняется. Поясним, с чем это связано.
Два выражения, значения которых равны при всех допустимых значениях входящих в них переменных, называются тождественно равными выражениями. Два числовых выражения, имеющие одинаковые значения, также называются тождественно равными.
В данном определении тождественно равных выражений стоит уточнить смысл фразы «при всех допустимых значениях входящих в них переменных». Она подразумевает все такие значения переменных, при которых одновременно имеют смысл оба тождественно равных выражения. Эту мысль разъясним в следующем пункте, рассмотрев примеры.
Определение тождественно равных выражений в учебнике Мордковича А. Г. дается немного иначе:
Тождественно равные выражения – это выражения, стоящие в левой и правой частях тождества.
По смыслу это и предыдущее определения совпадают.
Примеры тождественно равных выражений
Введенные в предыдущем пункте определения позволяют привести примеры тождественно равных выражений.
Однако области допустимых значений переменных в выражениях могут отличаться. Для примера возьмем выражения x−1 и 

Особую ценность имеет замена одного выражения другим, тождественно равным ему. Такая замена называется тождественным преобразованием выражения, эта тема в силу своей важности заслуживают детального рассмотрения в отдельной статье.
Тождественно равные выражения: определение, примеры
После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.
Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.
Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.
Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.
Можно указать еще и такое определение:
Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Для начала возьмем числовые выражения.
Так, 2 + 4 и 4 + 2 будут тождественно равными друг другу, поскольку их результаты будут равны ( 6 и 6 ).
Но область допустимого значения в одном выражении может отличаться от области другого.
Если мы заменяем одно выражение на другое, которое является тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и подробно о нем мы поговорим в отдельном материале.
Тождество
Тождество — это равенство, обе части которого являются тождественно равными выражениями. Тождества делятся на буквенные и числовые.
Тождественные выражения
Два алгебраических выражения называются тождественными (или тождественно равными), если при любых численных значениях букв они имеют одинаковую численную величину. Таковы, например, выражения:
Оба представленных выражения, при любом значении x будут равны друг другу, поэтому их можно назвать тождественными или тождественно равными.
Так же тождественными можно назвать и числовые выражения, равные между собой. Например:
Буквенные и числовые тождества
Буквенное тождество — это равенство, которое справедливо при любых значениях входящих в него букв. Другими словами, такое равенство, у которого обе части являются тождественно равными выражениями, например:
Числовое тождество — это равенство, содержащее только числа, выраженные цифрами, у которого обе части имеют одинаковую численную величину. Например:
Тождественные преобразования выражений
Все алгебраические действия представляют собой преобразование одного алгебраического выражения в другое, тождественное первому.
При вычислении значения выражения, раскрытии скобок, вынесении общего множителя за скобки и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения или просто преобразованием выражения. Все преобразования выражений выполняются на основе свойств действий над числами.
Рассмотрим тождественное преобразование выражения на примере вынесения общего множителя за скобки:
Выполнение данного преобразования основано на распределительном законе умножения.