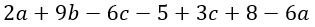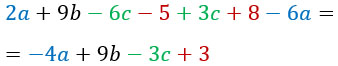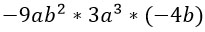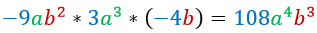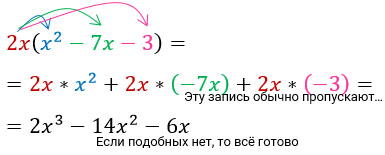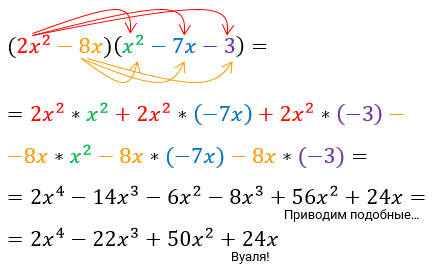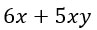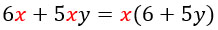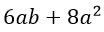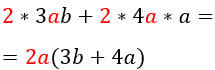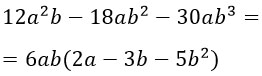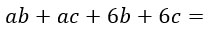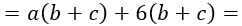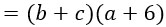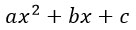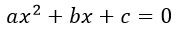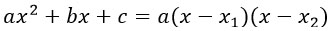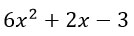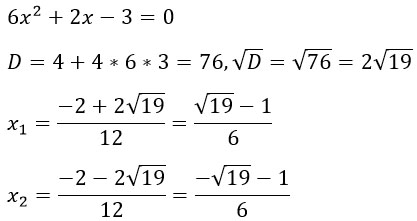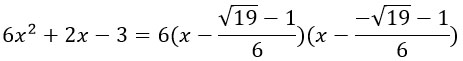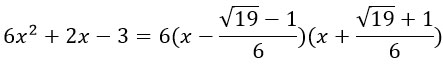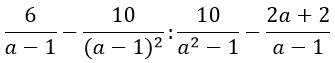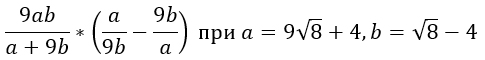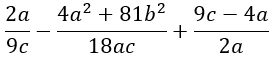Что значит упрощать выражение
Упрощение выражений
Одно из самых распространенных заданий в алгебре звучит так: «Упростите выражение». Сделать это можно используя один из ниже перечисленных приемов, но чаще всего тебе потребуется их комбинация.
Приведение подобных слагаемых.
Для примера упростим такое выражение:
Подобные слагаемые я выделю разными цветами и посчитаю. Кстати, знак перед слагаемым относится к этому слагаемому.
Как видишь, больше одинаковых буквенных частей нет. Выражение упрощено.
Умножение одночленов и многочленов.
При умножении одночленов используют правила умножения степеней.
Перемножим три одночлена:
Разными цветами выделю то, что буду последовательно перемножать.
Чтобы умножить одночлен на многочлен выражение за скобками умножить на каждое слагаемое в скобках. Подробности в следующем примере.
Осталось вспомнить умножение многочлена на многочлен. При таком вот умножении надо каждое слагаемое в первых скобках умножить на каждое слагаемое во вторых скобках, результаты сложить или вычесть в зависимости от знаков слагаемых.
Вынесение общего множителя за скобки.
Разбираться будем на примере.
Дано такое выражение:
Что общего у этих двух слагаемых? Правильно, в них обоих присутствует множитель x. Он и будет являться общим множителем, который надо вынести за скобку.
Возьмем другой пример.
Ну и давайте третий пример, только уже без комментариев.
Проверить правильность вынесения общего множителя за скобки можно путем раскрытия скобок (умножением).
Разложение многочлена на множители способом группировки.
Если надо разложить многочлен на множители, то способ группировки тебе пригодится.
Сгруппировать выражения можно лишь путем вынесения общих множителей за скобку. Но сделать это нужно так, чтобы скобки в итоге получились одинаковые. Зачем? Да затем, чтобы потом эти скобки вынести за другие скобки.
На примере будет яснее)
Беру пример самый простой, чисто для понимания того, что надо делать.
В первых двух слагаемых общим множителем является переменная а: выносим ее за скобку. Во вторых двух слагаемых общим множителем является число 6. Его тоже выносим за скобки.
Видишь получились две одинаковые скобки? Теперь они являются общим множителем. Выносим их за скобку и получаем милое произведение двух скобок:
Разложение квадратного трехчлена на множители.
Пусть дан квадратный трехчлен:
Чтобы разложить его на множители надо решить квадратное уравнение
Далее корни уравнения х1 и х2 подставить в следующую формулу:
Возьмем вот такой трехчлен:
Найдем корни квадратного уравнения.
Подставим их в формулу для разложения квадратного трехчлена на множители:
Что-то слишком много минусов во второй скобке. Чуть-чуть преобразуем ее:
Еще могут тебе пригодится:
— умение сокращать дроби;
А вот такие задания могут тебе встретится на экзамене.
2) Найти значение выражения при заданных значениях переменных:
3) Найти значение выражения при заданных значениях переменных:
Упрощения алгебраических выражений
Что значит упростить алгебраическое выражение
Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).
Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.
Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.
Правила упрощения алгебраических выражений
Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:
В процессе приведения выражения в более простую форму следует использовать полезные советы:
Приведение подобных
Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.
Подобными являются слагаемые (одночлены), которые обладают буквенной частью.
В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.
Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.
К примеру, приведем слагаемые:
Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.
Рассмотрим выражение с квадратной степенью:
Здесь число 3 является коэффициентом.
Разложение на множители
Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.
a b 2 + a 2 c = a b 2 + a c
В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.
Сокращение дроби
В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.
Объяснение алгоритм действий при сокращении дробей:
a a + b a 2 = a a + b a · a = a + b a
Важно заметить, что сокращению подлежат исключительно множители.
Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.
Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».
Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.
Сложение и вычитание дробей
При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:
a b + c d = a · d + c · b b · d ;
Разберем правило на конкретных примерах. Вычислим:
Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:
В данном случае общим множителем является число 24. Выполним преобразования и упростим выражение:
В данном примере следует смешанные дроби записать в виде неправильных. Далее можно упростить выражение по стандартному алгоритму:
Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:
Здесь общий множитель равен 12. Тогда:
a 2 b · 3 4 + a · 2 6 = 3 a 2 b + 2 a 12
Далее можно привести подобные в числители, и разложить на множители при их наличии:
a 2 b 4 + a 6 = 3 a 2 b + 2 a 12 = a 3 a b + 2 12
Когда знаменатели содержат буквы, схема действий существенно не меняется:
Рассмотрим пример, когда требуется упростить выражение:
Разложим знаменатели на множители:
a b 2 = a · b · b a 2 b = a · a · b
Вычислим единые множители:
a b 2 = a ¯ · b ¯ ¯ · b a 2 b = a ¯ · a · b ¯ ¯
Затем можно записать общие множители и выполнить умножение:
a ¯ · b ¯ ¯ · a · b = a 2 b 2
1 a b 2 · a + 1 a 2 b · b = a + b a 2 b 2
Умножение и деление дробей
Умножение и деление дробей выполняют таким образом:
a b · c d = a · c b · d ;
a b : c d = a · d b · c
Арифметические действия выполняют в следующем порядке:
Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.
Используя правило умножения и деления дробей, получим:
Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.
Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.
Попробуем упростить выражение:
Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:
Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:
Пояснения на примерах
Требуется упростить выражения:
Приведем подобные и упростим выражения:
Заметим, что ab и 2ba являются подобными по той причине, что:
В результате можно сделать вывод, что данные слагаемые обладают одинаковой буквенной частью.
Требуется упростить выражения:
Путем разложения на множители упростим данные выражения:
a b 2 + a 2 c = a b 2 + a c
72 30 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 3 5 = 12 5
a a + b a 2 = a a + b a · a = a + b a
В первую очередь выполним разложение на множители:
Дано выражение, которое требуется упростить:
В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:
Рассмотрим выражение на наличие общих множителей:
Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:
Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:
Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:
x 2 + 2 x + 4 = x 2 + 2 · x + 2 2
Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:
Требуется упростить выражения:
Дано выражение, которое требуется упростить:
При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:
a во второй степени;
x в третьей степени;
b в третьей степени;
y в четвертой степени.
В результате получим:
Нужно упростить выражение:
Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.
Выглядит этот алгоритм таким образом:
Как упростить алгебраическое выражение
Некоторые алгебраические примеры одним видом способны наводить ужас на школьников. Длинные выражения не только пугают, но и очень затрудняют вычисления. Пытаясь сходу понять, что и за чем следует, недолго запутаться. Именно по этой причине математики всегда стараются максимально упростить «жуткое» задание и только потом приступают к его решению. Как ни странно, такой трюк значительно ускоряет процесс работы.
Упрощение является одним из фундаментальных моментов в алгебре. Если в простых задачах без него ещё можно обойтись, то более трудные для вычисления примеры могут оказаться «не по зубам». Тут-то и пригодятся эти навыки! Тем более что сложных математических знаний не требуется: достаточно будет всего лишь запомнить и научиться применять на практике несколько базовых приёмов и формул.
Необходимые знания и умения
Вне зависимости от сложности вычислений при решении любого выражения важно соблюдать порядок выполнения операций с числами:
Последние два пункта можно спокойно поменять местами и это никак не отразится на результате. Но складывать два соседних числа, когда рядом с одним из них стоит знак умножения категорически нельзя! Ответ если и получится, то неверный. Поэтому нужно запомнить последовательность.
Применение подобных
К таким элементам относятся числа с переменной одного порядка или одинаковой степени. Существуют и так называемые свободные члены, не имеющие рядом с собой буквенного обозначения неизвестного.
Суть заключается в том, что при отсутствии скобок можно упростить выражение, складывая или вычитая между собой подобные.
Несколько наглядных примеров:
Разложение числа на множители
Эта маленькая математическая хитрость, если научиться её правильно использовать, в будущем не раз поможет справиться с каверзной задачкой. Да и понять, как работает «система», несложно: разложением называют произведение нескольких элементов, вычисление которого даёт исходное значение. Таким образом, 20 можно представить как на 20×1, 2×10, 5×4, 2×5×2 или другим способом.
На заметку: множители всегда совпадают с делителями. Так что искать рабочую «пару» для разложения нужно среди чисел, на которые исходное делится без остатка.
Проделывать такую операцию можно как со свободными членами, так и с цифрами при переменной. Главное, не потерять последнюю во время вычислений — даже после разложения неизвестная не может взять и «уйти в никуда». Она остаётся при одном из множителей:
Простые числа, которые можно разделить лишь на себя или 1, никогда не раскладываются — в этом нет смысла.
Основные способы упрощения
Первое, за что цепляется взгляд:
Алгебраические примеры в школьной программе часто составляются с учётом того, что их можно красиво упростить.
Вычисления в скобках
Внимательно следите за знаком, стоящим перед скобками! Умножение или деление применяется к каждому элементу внутри, а минус — меняет имеющиеся знаки «+» или «-» на противоположные.
Скобки вычисляются по правилам либо по формулам сокращённого умножения, после чего приводятся подобные.
Сокращение дробей
Сокращать дроби тоже несложно. Они сами через раз «охотно убегают», стоит произвести операции с приведением подобных членов. Но упростить пример можно ещё до этого: обращайте внимание на числитель и знаменатель. Они нередко содержат явные или скрытые элементы, которые можно взаимно сократить. Правда, если в первом случае нужно всего лишь вычеркнуть лишнее, во втором придётся подумать, приводя часть выражения к виду для упрощения. Используемые методы:
Когда выражение или его часть находится под корнем, первостепенная задача упрощения практически аналогична случаю с дробями. Необходимо искать способы полностью от него избавиться или, если это невозможно, максимально сократить мешающий вычислениям знак. Например, до ненавязчивого √(3) или √(7).
Верный способ упростить подкоренное выражение — попытаться разложить его на множители, часть из которых выносится за пределы знака. Наглядный пример: √(90)=√(9×10) =√(9)×√(10)=3√(10).
Другие маленькие хитрости и нюансы:
Упрощение степенного выражения
Если в случае простых вычислений на минус или плюс примеры упрощаются за счёт приведения подобных, то как быть при умножении или делении переменных с разными степенями? Их можно легко упростить, запомнив два основных момента:
Единственное условие для такого упрощения — одинаковое основание у обоих членов. Примеры для наглядности:
Отмечаем, что операции с числовыми значениями, стоящими перед переменными, происходят по обычным математическим правилам. И если присмотреться, то становится понятно, что степенные элементы выражения «работают» аналогично:
Как и в любом деле, при упрощении алгебраических выражений необходимо не только знание основ, но и практика. Уже через несколько занятий примеры, когда-то кажущиеся сложными, будут сокращаться без особого труда, превращаясь в короткие и легко решаемые.
Видео
Это видео поможет вам разобраться и запомнить, как упрощаются выражения.
Упрощение выражений
Свойства сложения, вычитания, умножения и деления полезны тем, что позволяют преобразовывать суммы и произведения в удобные выражения для вычислений. Научимся, как можно с помощью этих свойств упрощать выражения.
В этом выражении есть числа, при сложении которых получаются «круглые» числа. Заметив это, легко провести вычисления устно. Воспользуемся переместительным законом сложения.
Также для упрощения вычисления произведений можно использовать переместительный закон умножения.
Сочетательные и переместительные свойства используются и при упрощении буквенных выражений.
Распределительный закон умножения часто применяется для упрощения вычислений.

Применяя распределительное свойство умножения относительно сложения или вычитания к выражению « (a + b) · с и (a − b) · c », мы получаем выражение, не содержащее скобки.
В этом случае говорят, что мы раскрыли (опустили) скобки. Для применения свойств не имеет значения, где записан множитель « c » — перед скобками или после.
Раскроем скобки в выражениях.
Вынесение общего множителя за скобки
Поменяем местами правую и левую часть равенства:
В таких случаях говорят, что из « ac + bc » вынесен общий множитель « с » за скобки.
Примеры вынесения общего множителя за скобки.
Упрощения выражений — формулы и примеры для 5 класса
В математике применяется специальная операция — упрощение выражений. Формулы для 5 класса позволяют решать тождества, приводя их к оптимальному виду. Этот навык пригодится при решении задач по другим дисциплинам с физико-математическим уклоном в школе, а также в высших учебных заведениях. Однако перед изучением алгоритмов, необходимо ознакомиться с теоретическим материалом.
Общие сведения
Принцип решения любой математической задачи основан на получении оптимального ответа, который в дальнейшем возможно будет применить для других целей (доказательства теорем, тождеств, получения промежуточных величин). Оптимизация результата состоит из операций, имеющих собственный приоритет. Последний соответствует порядковому номеру элемента в списке:
В первом случае компоненты выражения группируются посредством скобок. В математике принято использовать только круглые, т. е. «()». Однако допускаются квадратные «[]», но некоторые начинающие математики иногда группируют элементы выражения при помощи фигурных скобок «<>». Это делать не рекомендуется, поскольку последние обозначают в дисциплинах с физико-математическим уклоном общее решение.
Иногда новички не знают, что возведение в степень и извлечение корня являются двумя эквивалентными операциями. Это утверждение легко доказывается. Например, квадратный корень из 36 эквивалентен 6. Знак радикала можно заменить степенью, имеющей вид обыкновенной или десятичной дроби, т. е. (36)^(½)=√36=6.
Произведение не всегда обладает высшим приоритетом, чем деление. Для удобства вычислений можно сначала разделить, а затем умножить. Например, требуется найти значение выражения «3*81:9». Его можно решить, основываясь на приоритетах или удобстве вычислений (оптимизации). Для сравнения расчетов нужно решить равенство двумя способами:
При решении получены одинаковые результаты. Следует отметить, что простой метод — второй. Операции сложения и вычитания имеют одинаковый приоритет. Упростить выражение — означает, что необходимо преобразовать его из сложной формы представления в простую. Иными словами, операция называется оптимизацией результата.
Оптимизация выражений применяется при решении уравнений (равенств с неизвестными величинами) любой сложности и доказательства теорем. Это базовые знания, необходимые для упрощения выражений в 5 классе.
Базовые знания
Для освоения определенного направления в любой дисциплине необходимы определенные знания. Например, невозможно выполнить умножение одного числа на другое, не зная таблицы умножения. Это касается и оптимизации тождеств. Основные элементы теории, которые нужно знать для выполнения операции:
По этим пунктам можно упрощать алгебраические целочисленные и дробные выражения любой сложности. Однако каждый из элементов необходимо разобрать подробно, чтобы не совершать ошибок при расчетах.
Приведение подобных элементов
Практически во всех заданиях нужно складывать общие элементы, полученные при расчетах или раскрытии скобок. Для этой операции необходимо руководствоваться следующими правилами:
В первом случае нужно привести пример тождества следующего вида: 2+5t+4+5t^2+2t-4t^2. Чтобы его упростить, необходимо сгруппировать подобные компоненты, т. е. (2+4)+(5t+2t)+(5t^2-4t^2). Далее следует сложить компоненты между собой, т. е. 6+7t+t^2.
Группу «5t^2-4t^2» можно назвать операцией сложения, хотя на самом деле она называется разностью, которую записывают и в виде суммы: 5t^2+(-4t^2). Раскрывая скобки в последнем тождестве, можно получить упрощенную форму: 5t^2-4t^2. Далее необходимо ознакомиться с правилами раскрытия скобок.
Раскрытие скобок
Операция раскрытия скобок для выполнения дальнейших вычислений очень часто применяется в различных дисциплинах с физико-математическим уклоном. Она осуществляется по следующим правилам:
В первом и втором случаях операции называют вынесением общего множителя за скобки. Последнее правило группировки действует не на все компоненты, т. е невозможно выполнить объединение 2 и 3 элементов (5 и 4) в выражении «4:5+4-1+7». Для доказательства следует решить его двумя способами:
Выражение, решенное первым и вторым способом, имеет различные ответы, поскольку 10,8>6[4/9]. Объяснение этому несоответствию — нарушение логики тождества. Следующим компонентом, составляющим базу для упрощения тождеств, является работа со степенями.
Работа со степенями
В математических тождествах иногда необходимо упростить степенные выражения. Однако большинство математиков-новичков делает много ошибок, поскольку не знают основных правил:
Нулевое значение в такой же степени является пустым множеством, т. е. его не существует. Cтепень может быть представлена в виде обыкновенной или десятичной дроби. В последнем случае для удобства ее необходимо перевести к первому типу. Если указано значение степенного показателя, равное 3/5, нужно величину возвести в куб, а затем изъять корень 5 порядка.
Оптимизация обыкновенных дробей
Практически во всех заданиях или тренажерах большая часть примеров представлена в виде обыкновенной дроби вида s/t, которую нужно сократить. Иногда необходимо произвести операции произведения или деления одной величины на другую (буквенное обозначение — s/t и w/v), а также сложения и вычитания. При последних операциях всегда необходимо приводить дробные тождества к общему знаменателю. Эта операция осуществляется следующим образом:
В последнем случае каждый знаменатель необходимо разложить на множители, затем перемножить между собой все неповторяющиеся компоненты. Следующим элементом, который необходимо для преобразования тождеств, являются формулы сокращенного умножения.
Сокращенное умножение
Для решения задач очень часто применяются формулы сокращенного умножения. В некоторых случаях тождества «собираются» в них или, наоборот, для сокращения нужно расписать элементы по множителям (правая часть равенства). Соотношения имеют следующий вид:
Cледует отметить, что в некоторых случаях к формуле сокращенного умножения тождество следует «подвести», воспользовавшись свойством отнимания и прибавления одного и того же значения. Например, необходимо из некоторого выражения (2t^2-60) выделить одну из формул. Это делается следующим образом:
Иногда в более сложных выражениях приходится применять несколько соотношений. Если тождество является дробью, обязательно следует проверить условие неравенства знаменателя нулевой величине. Для этой цели следует решить соответствующее уравнение, вычислив его корни. Последние должны привести к пустому множеству, т. к. на 0 делить нельзя. Вот именно их и необходимо исключить, записав условие, т. е. t!=-9.
Таким образом, для грамотной оптимизации математических выражений необходимо пользоваться рекомендациями специалистов, правилами и методиками, поскольку их несоблюдение могут существенно повлиять на результаты вычислений.